C++实现ransac

目录

一、ransac算法原理

1.1、算法概念

1.2、图解

二、c++实现ransac

2.1、设置随机样本和离群点

2.2、随机抽取样本

2.3、内点计算

2.4、更新参数

2.2、完整代码

---

一、ransac算法原理

1.1、算法概念

        随机抽样一致性 (RANSAC) 是一种迭代方法，用于根据一组包含异常值的观测数据来估计数学模型的参数，此时异常值不会对估计值产生影响。 因此，它也可以解释为一种异常值检测方法，说白了就是能剔除异常的、离群的样本。 它是一种非确定性算法，因为它仅以一定的概率产生合理的结果，并且随着允许更多迭代，该概率会增加，说白了就是由于每次随机抽取样本，最终都会得到更好的结果，但是每次执行整个ransac算法，最终结果会有略微差异。 该算法最初由 Fischler 和 Bolles 在 SRI International 于 1981 年发布。他们使用 RANSAC 来解决位置确定问题 (LDP)，其目标是确定空间中投影到图像上的点，形成一组地标 已知地点。

        一个基本假设是数据由“内点”和“离群值”组成，“内点”是指其分布可以通过某些模型参数集来解释的数据，尽管可能会受到噪声的影响；“离群值”是不适合模型的数据。 例如，异常值可能来自噪声的极值、错误的测量或有关数据解释的错误假设。 RANSAC 还假设，给定一组（通常很小的）内点，存在一个可以估计模型参数的过程，该模型可以最佳地解释或拟合该数据。

伪代码：

Given:
    data – a set of observations
    model – a model to explain observed data points
    n – minimum number of data points required to estimate model parameters
    k – maximum number of iterations allowed in the algorithm
    t – threshold value to determine data points that are fit well by model
    d – number of close data points required to assert that a model fits well to data

Return:
    bestFit – model parameters which best fit the data (or nul if no good model is found)

iterations = 0
bestFit = nul
bestErr = something really large
while iterations < k {
    maybeInliers = n randomly selected values from data
    maybeModel = model parameters fitted to maybeInliers
    alsoInliers = empty set
    for every point in data not in maybeInliers {
        if point fits maybeModel with an error smaller than t
             add point to alsoInliers
    }
    if the number of elements in alsoInliers is > d {
        % this implies that we may have found a good model
        % now test how good it is
        betterModel = model parameters fitted to all points in maybeInliers and alsoInliers
        thisErr = a measure of how well betterModel fits these points
        if thisErr < bestErr {
            bestFit = betterModel
            bestErr = thisErr
        }
    }
    increment iterations
}
return bestFit

1.2、图解

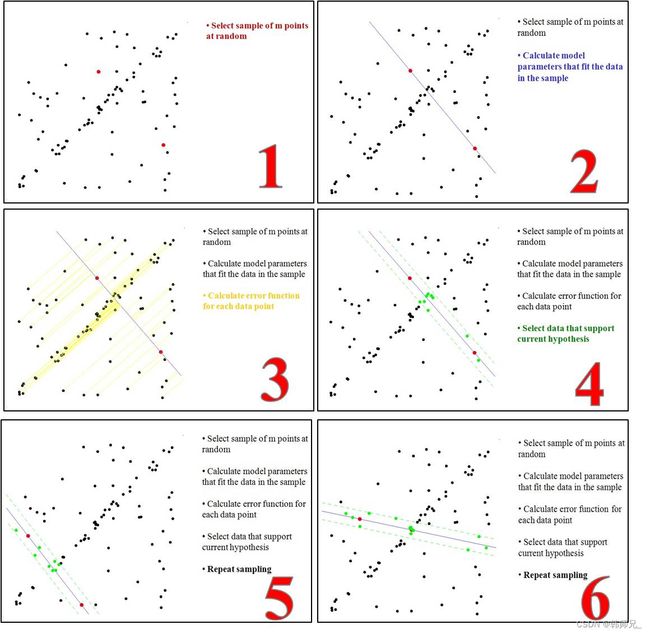
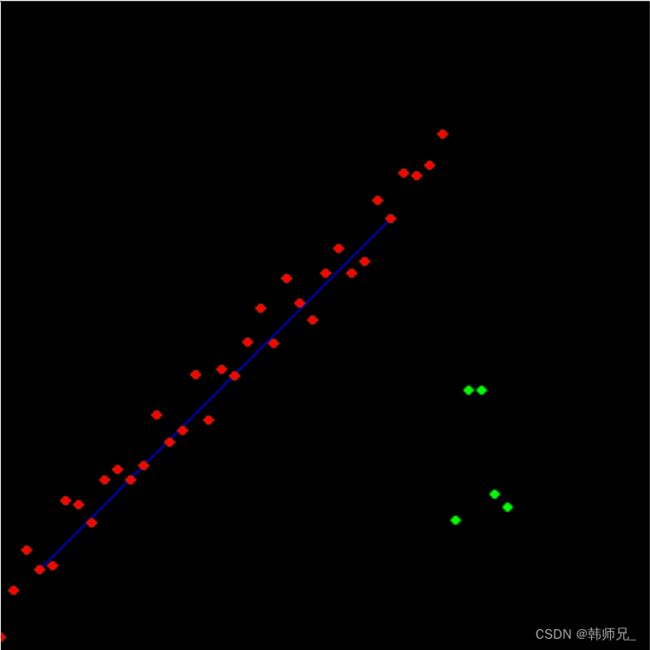
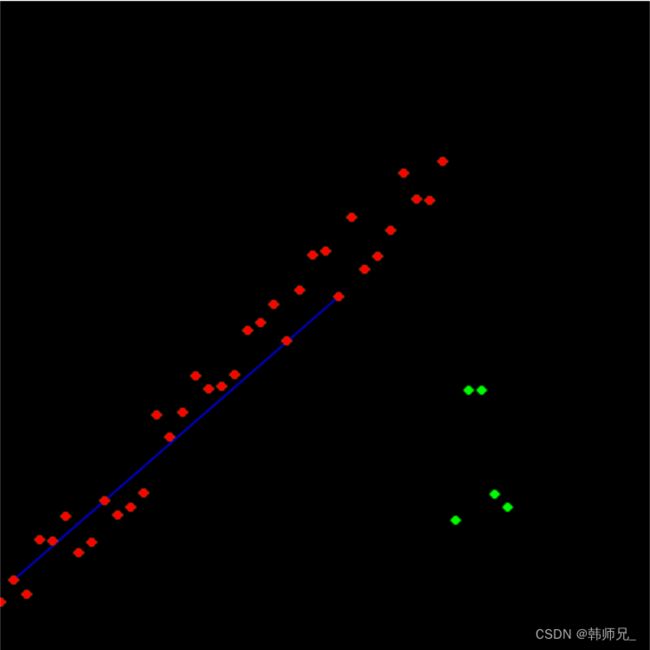
        如下图，以直线拟合为例子，假如给定N个点，求解直线方程y=kx+b。这里使用ransac算法求解直线方程参数k、b，主要思想如下：

• step1:随机选取两个样本点，如图红点
• step2:计算直线方程参数ki、bi，得到直线记为Li，此时有k=ki,b=bi
• step3:计算其余所有点到直线Li的距离，距离Li足够近的点为内点（inliers），比较远的点为外点（outliers）
• step4:执行step1、step2得到直线Lj（对应方程参数kj、bj）；执行step3得到的inliers如果大于直线Li，那么更新参数为：k=kj,b=bj。

        依次类推，最多循环迭代100次，只要下一次计算得到直线比上一次更优，那就更新参数k、b；直到内点比例足够高或者循环到100次了为止。

二、c++实现ransac

依赖opencv的一点点数据结构，你也可以自己去掉。

2.1、设置随机样本和离群点

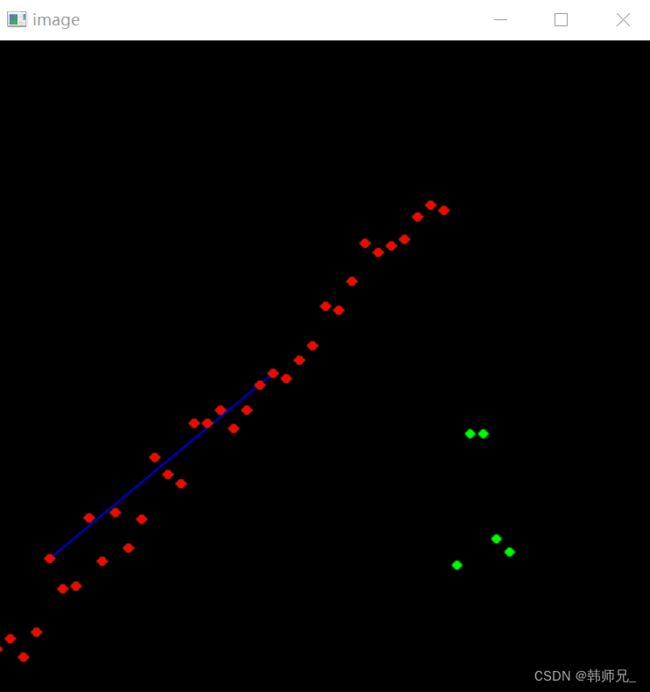
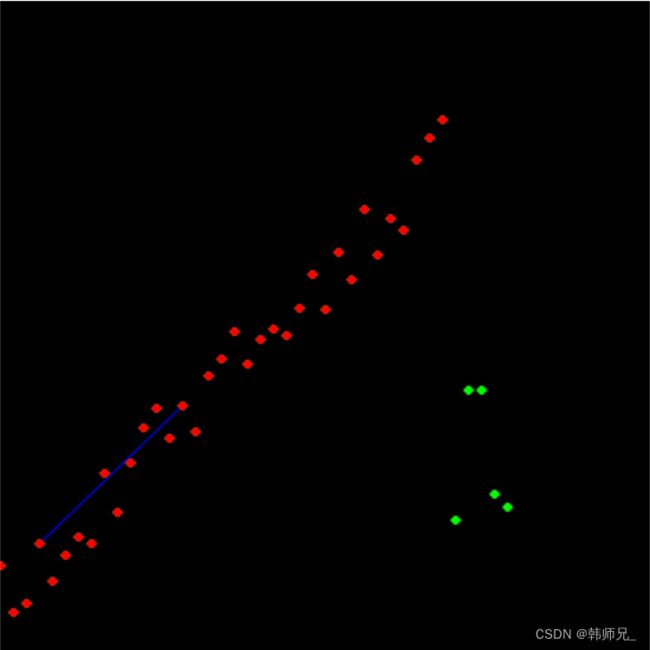
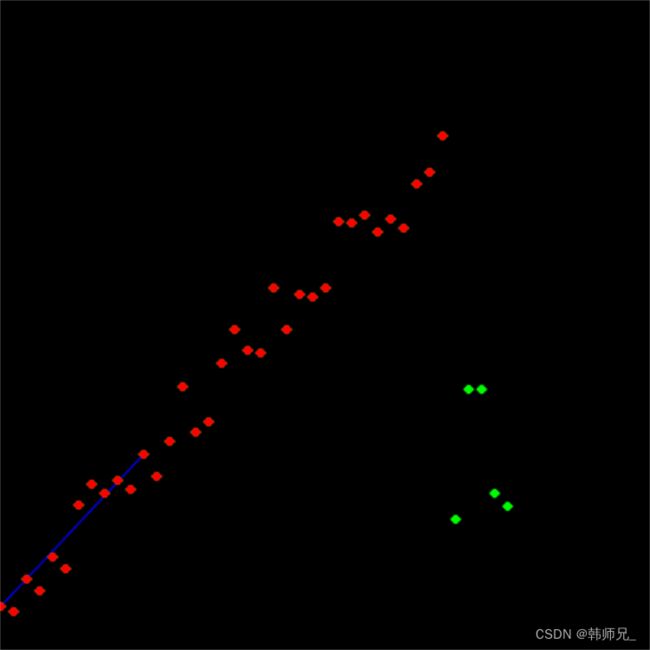
如下图，红色点就是样本点，绿色的就是离群点

// time seed
srand((unsigned int)time(nullptr));
// <1>产生随机数
vector points;
// 精确解
const int k = 1;
const int b = 10;

// x [0, 390]; y [10, 400] total_numbers = 40
for (int x = 0; x < 400; x += 10)
{
	points.push_back(Point2d(x, k * x + b + Ransac::getRand(0, 60)));
}
//添加离群点
points[35].y = 100;
points[36].y = 200;
points[37].y = 200;
points[38].y = 120;
points[39].y = 110;

2.2、随机抽取样本

随机选取两个样本点的索引。

// <1>、随机抽取两个样本
int index_first = Ransac::getRand(0, points.size() - 2);
int index_second = Ransac::getRand(0, points.size() - 2);
sample_first = points[index_first];
sample_second = points[index_second];

2.3、内点计算

y_error实在计算点到直线距离，如果小于y_threshold，也就是内点inliers。

// <2>、根据距离，来找出所有样本点中的内点，并统计数量
for (int i = 0; i < points.size(); i++)
{
	// delta = k * x  + b - y
	double y_error = abs(k_estimate * points[i].x + b_estimate - points[i].y) / sqrt((pow(k_estimate, 2) + 1));
	//cout << "y_error = " << y_error << endl;
	if (y_error < y_threshold)
	{
		count++;
	}
}

2.4、更新参数

如果当前迭代比上一轮内点要多，那直接当当前迭代对应参数更新为最优解

//  <3>、找出内点数量最多的那一组
if (count > total)
{
	total = count;

	best_sample_first = sample_first;
	best_sample_second = sample_second;

	best_parameters.x = k_estimate;
	best_parameters.y = b_estimate;
}

2.2、完整代码

需要说明：

• ransac每次结果不一样，但是总是能计算得到好的解；
• 以下代码在画直线的时候没有画得很长，并不影响算法，只是懒得画而已。

完整代码：

#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
#include
using namespace std;
#include
using namespace cv;
// 功能：画点
void drawPoints(vector points, Mat& image, bool is_green)
{
    if (is_green)
    {
        for (int i = 0; i < points.size(); i++)
        {
            circle(image, Point2i(int(points[i].x), int(points[i].y)), 2, cv::Scalar(0, 255, 0), 2, LINE_AA);
        }
    }
    else
    {
        for (int i = 0; i < points.size(); i++)
        {
            circle(image, Point2i(int(points[i].x), int(points[i].y)), 2, cv::Scalar(0, 0, 255), 2, LINE_AA);
        }
    }

}
// 功能：画线
void drawLine(Point2d begin, Point2d end, Mat& image)
{
    line(image, Point2i(int(begin.x), int(begin.y)),
        Point2i(int(end.x), int(end.y)), Scalar(255, 0, 0), 1, LINE_AA);
}
// 功能：将一张图经行纵向镜像
void upDownMirror(Mat& image)
{
    Mat image_cpy = image.clone();
    for (int j = 0; j < image.rows; j++)
    {
        for (int i = 0; i < image.cols; i++)
        {
            image.ptr(j)[i] = image_cpy.ptr(image.rows - 1 - j)[i];
        }
    }
}
// 功能：最简单的直线拟合 Ransac 框架
class Ransac
{
public:
    Ransac(vector x, vector y);
    ~Ransac();
    static int getRand(int min, int max);//[min, min + max - 1]
public:
    vector x_, y_;
};

Ransac::Ransac(vector x, vector y) :x_(x), y_(y)
{

}

Ransac::~Ransac()
{

}

int Ransac::getRand(int min, int max)//[min, min + max - 1]
{
    return rand() % max + min;
}

int main()
{
    // time seed
    srand((unsigned int)time(nullptr));

    // <1>产生随机数
    vector points;
    // 精确解
    const int k = 1;
    const int b = 10;

    // x [0, 390]; y [10, 400] total_numbers = 40
    for (int x = 0; x < 400; x += 10)
    {
        points.push_back(Point2d(x, k * x + b + Ransac::getRand(0, 60)));
    }
    //添加离群点
    points[35].y = 100;
    points[36].y = 200;
    points[37].y = 200;
    points[38].y = 120;
    points[39].y = 110;
    const int itr_nums = 300;
    double k_estimate = 0;
    double b_estimate = 0;
    Point2d best_parameters; // [k, b]
    // 统计纵向距离 y
    int count = 0; // 内点计数器
    int y_threshold = 50; // 判定内点的阈值
    int total = 0; // 内点总数
    //样本点
    Point2d sample_first;
    Point2d sample_second;
    // 最佳样本点
    Point2d best_sample_first;
    Point2d best_sample_second;
    for (int i = 0; i < itr_nums; i++)
    {
        // <1>、随机抽取两个样本
        int index_first = Ransac::getRand(0, points.size() - 2);
        int index_second = Ransac::getRand(0, points.size() - 2);
        sample_first = points[index_first];
        sample_second = points[index_second];

        if (sample_first == sample_second)
        {
            continue;
        }
        // 计算斜率 k = (y2 - y1)/(x2 - x1)
        k_estimate = (sample_second.y - sample_first.y) / (sample_second.x - sample_first.x);
        // 计算截距 b = y1 - k * x1
        b_estimate = sample_first.y - k_estimate * sample_first.x;
        // <2>、根据距离，来找出所有样本点中的内点，并统计数量
        for (int i = 0; i < points.size(); i++)
        {
            // delta = k * x  + b - y
            double y_error = abs(k_estimate * points[i].x + b_estimate - points[i].y) / sqrt((pow(k_estimate, 2) + 1));
            //cout << "y_error = " << y_error << endl;
            if (y_error < y_threshold)
            {
                count++;
            }
        }
        //  <3>、找出内点数量最多的那一组
        if (count > total)
        {
            total = count;

            best_sample_first = sample_first;
            best_sample_second = sample_second;

            best_parameters.x = k_estimate;
            best_parameters.y = b_estimate;
        }
        count = 0;
    }
    cout << "内点数 = " << total << endl;
    cout << "斜率 k = " << best_parameters.x << "截距 b = " << best_parameters.y << endl;

    // 统计内点
    vector inliners_points;
    for (int i = 0; i < points.size(); i++)
    {
        // delta = k * x  + b - y
        double y_error = abs(best_parameters.x * points[i].x + best_parameters.y - points[i].y) / sqrt((pow(k_estimate, 2) + 1));
        //cout << "y_error = " << y_error << endl;
        if (y_error < y_threshold)
        {
            inliners_points.push_back(points[i]);
        }
    }
    Mat image = Mat::zeros(500, 500, CV_8UC3);
    drawLine(best_sample_first, best_sample_second, image);
    drawPoints(points, image, true);
    drawPoints(inliners_points, image, false); //画内点
    upDownMirror(image);
    imshow("image", image);
    waitKey(0);
    return 1;
}