0-1背包【多种算法解答(手工运算及完整源码)】
目录
1.问题描述
2.问题解析及完整源码
(1)二维DP
(2)一维DP
(3)回溯法
(4)部分背包问题(贪心)
3.手工运算
(1)动态规划
(2)回溯
1.问题描述
有 N 件物品和一个容量是V的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi ,价值是 wi 。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
2.问题解析及完整源码
(1)二维DP
(1)状态f[i][j]定义:前 i 个物品,背包容量 j 下的最优解(最大价值):
当前的状态依赖于之前的状态,可以理解为从初始状态f[0][0] = 0开始决策,有 N 件物品,则需要 N 次决 策,每一次对第 i 件物品的决策,状态f[i][j]不断由之前的状态更新而来。
(2)当前背包容量不够(j < v[i]),没得选,因此前 i 个物品最优解即为前 i−1 个物品最优解:对应代码:f[i][j] = f[i - 1][j]。
(3)当前背包容量够,可以选,因此需要决策选与不选第 ii 个物品:选:f[i][j] = f[i - 1][j - v[i]] + w[i]。
不选:f[i][j] = f[i - 1][j] 。
我们的决策是如何取到最大价值,因此以上两种情况取 max() 。
#include
using namespace std;
const int MAXN = 1005;
int v[MAXN]; // 体积
int w[MAXN]; // 价值
int f[MAXN][MAXN]; // f[i][j], j体积下前i个物品的最大价值
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
{
// 当前背包容量装不进第i个物品,则价值等于前i-1个物品
if (j < v[i])
f[i][j] = f[i - 1][j];
// 能装,需进行决策是否选择第i个物品
else
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
(2)一维DP
将状态f[i][j]优化到一维f[j],实际上只需要做一个等价变形。
为什么可以这样变形呢?我们定义的状态f[i][j]可以求得任意合法的i与j最优解,但题目只需要求得最终状态f[n][m],因此我们只需要一维的空间来更新状态。
(1)状态f[j]定义:N 件物品,背包容量j下的最优解。
(2)注意枚举背包容量j必须从m开始。
(3)为什么一维情况下枚举背包容量需要逆序?在二维情况下,状态f[i][j]是由上一轮i - 1的状态得来的,f[i][j]与f[i - 1][j]是独立的。而优化到一维后,如果我们还是正序,则有f[较小体积]更新到f[较大体积],则有可能本应该用第i-1轮的状态却用的是第i轮的状态。
(4)例如,一维状态第i轮对体积为 3 的物品进行决策,则f[7]由f[4]更新而来,这里的f[4]正确应该是f[i - 1][4],但从小到大枚举j这里的f[4]在第i轮计算却变成了f[i][4]。当逆序枚举背包容量j时,我们求f[7]同样由f[4]更新,但由于是逆序,这里的f[4]还没有在第i轮计算,所以此时实际计算的f[4]仍然是f[i - 1][4]。
(5)简单来说,一维情况正序更新状态f[j]需要用到前面计算的状态已经被「污染」,逆序则不会有这样的问题。
状态转移方程为:f[j] = max(f[j], f[j - v[i]] + w[i] 。
实际上,只有当枚举的背包容量 >= v[i] 时才会更新状态,因此我们可以修改循环终止条件进一步优化。
关于状态f[j]的补充说明
二维下的状态定义f[i][j]是前 i 件物品,背包容量 jj 下的最大价值。一维下,少了前 i 件物品这个维度,我们的代码中决策到第 i 件物品(循环到第i轮),f[j]就是前i轮已经决策的物品且背包容量 j 下的最大价值。因此当执行完循环结构后,由于已经决策了所有物品,f[j]就是所有物品背包容量 j 下的最大价值。即一维f[j]等价于二维f[n][j]。
#include
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main() {
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j-v[i]]+w[i]);
cout << f[m] << endl;
return 0;
}
(3)回溯法
●0-1背包问题属于找最优解问题,适合于用子集树表示0-1背包问题的解空间。
●在搜索解空间树时,只要其左儿子节点是一个可行结点,搜索就进入左子树。在右子树中有可能包含最优解是才进入右子树搜索,否则将右子树剪去。
●设r是当前剩余物品价值总和;cp是当前结点的价值; bestp是当前最优价值。当cp+rsbestp时,可剪去以当前结点为根的子树。
●计算右子树中解的上界的更好方法是将剩余物品依其单位重量价值排序,然后依次装入物品,直至装不下时,再装入该物品的一部分而装满背包。由此得到的价值是右子树中解的上界。
Backtrack(int i) {
if (i > n)
{
bestp = cp; return;
}//bestp表示当前最优解的装包价值,初值为0。能走到这儿,意味着得到更优解,因此才改写。
if (cw + w[i] <= c)
{
cw += w[i; cp += p[i];
Backtrack(i + 1);
cw=w[i];
cp+=p[i];
}//cw和cp是全局变量,表示当前路径已装包重量及装包价值,初值均为0。
if (Bound(i + 1) > bestp)
{
Backtrack(i + 1);
}
Bound(int i)
{
cleft = c - cw;//剩余容量
b = cp;//以物品单位重量价值递减序装入物品
while (i <= n && w[i] <= cleft)
{
cleft - = w[i];
b + = p[i];
i++;
}//装满背包
if (i <= n) b + —p[i] / w[i] * cleft;
{
return b;
}(4)部分背包问题(贪心)
void KNAPSACK(int n, float c, float v[], float w[], float x[])
//v[],w[]分别含有v[i]/w[i]>=v[i+1]/w[i+1]排序的n件物品的效益值和重量;c是背包的容量,x[]是解向量
{
int i;
for (i = 1; i <= n; i++)
{
x[i] = 0;//将解向量初始化为0
}
float cu = c;//cu是背包剩余容量
for (i = 1; i <= n; i++)
{
if (w[i] > cu)break;
x[i] = 1;
cu = cu - w[i];
}
if (i <= n)x[i] = cu/w[i];
}3.手工运算
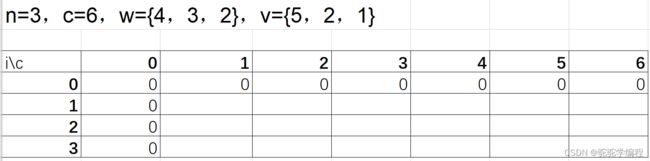
(1)动态规划
1.列出表格,此时放入0个物品,此时产生的价值当然为0
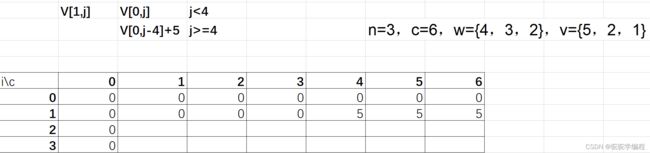
2.放入第一个背包,当背包容量为0,1,2,3的时候,都放不下第一个容量为4的物品,产生的价值为0,当背包容量大于等于4的时候可以放下这个物品,所产生的价值为5
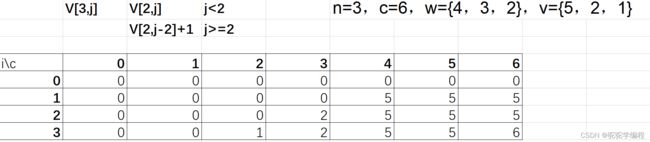
3.放入前两个物品,当背包容量为0,1,2的时候都放不下这两个物品,当背包容量为3,放得下第二个物品,所产生的价值为2,当背包容量继续增大,可以放下第一个物品,所产生的价值为5
4.放入三个物品,当背包容量为0,1的时候不能放下任何一个物品,当背包容量为2的时候可以放下第三个物品,产生是价值为1,当背包容量为3的时候可以放下第二个物品,所产生的价值为2,当背包容量为4的时候,可以放下第一个物品,所产生的价值为5,当背包容量为5的时候可以放下第一个物品或者第二和第三个物品,所产生的价值分别为5和3,进过比较,存放第一个物品。当背包容量为6的时候,可以放下多种情况的物品,经过比较,放入第一和第三个物品产生的价值最大,为6
值得注意的是算法运行的时候并不是一步一步的进行运算的,它使用到了动态规划,他的核心表达式为 f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]),它进行的每一步都在比较方案之间的大小
(2)回溯
对于0-1背包问题回溯法的一个实例,n=4, c=7,p=[9,10,7,4],w=[3,5,2,1]。这4个物品的单位重量价值分别为[3,2,3.5,4]。以物品为单位价值的递减序装入物品。先装入物品4,然后装入物品3和1。装入这3个物品后,剩余的背包容量为1,只能装入0.2个物品2。由此可得到一个解为x=[1,0.2,1,1],其相应的价值为22。尽管这不是一个可行解,但可以证明其价值是最有大的上界。因此,对于这个实例,最优值不超过22。
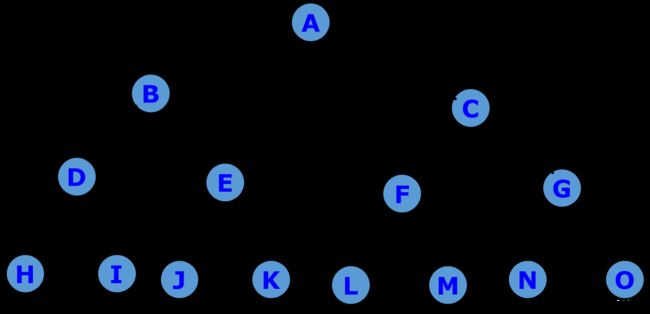
对于n=3时的0-1背包问题,其解空间用一棵完全二叉树表示,如下图所示。