DL Homework 7
目录
一、用自己的语言解释以下概念
局部感知、权值共享
池化(子采样、降采样、汇聚)。会带来那些好处和坏处?
全卷积网络
低级特征、中级特征、高级特征
多通道。N输入,M输出是如何实现的?
1×1的卷积核有什么作用
二、使用CNN进行XO识别
1 复现资料中的代码
1.1 X图像的生成
1.2 卷积核的初始化
1.3 卷积
1.3.1 空洞卷积
1.4 池化
1.5 激活
2、利用CNN对XO数据集进行训练+测试
2.1 数据集
2.2 模型构建
2.3 模型训练
2.4 模型测试
2.5 计算模型的准确率
2.6 查看训练好的模型的特征图
2.7 查看训练好的模型的卷积核
3 重新设计网络结构
3.1 至少增加一个卷积层,卷积层达到三层以上
3.2 去掉池化层,对比“有无池化”的效果
3.3 修改“通道数”等超参数,观察变化
4 可视化
探索低级特征、中级特征、高级特征
总结
参考博客
一、用自己的语言解释以下概念
局部感知、权值共享
局部感知和权值共享是卷积神经网络的两大特性。
有一篇博客在这儿讲的贼好,图是博客中用到的,这里引用一下
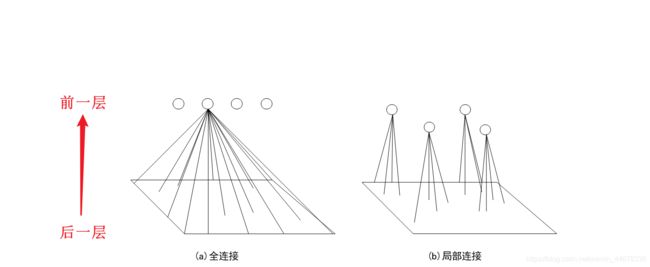
局部感知:图中(a)表示的神经元之间的全连接的结构,这样前后两层神经元之间都是互相连接的,后一层的每一个神经元一定具有前一层神经元的所有信息,这也就意味着需要储存很多的参数;而图(b)表示神经元之间进行局部连接,即前面一层神经元只与后一层的部分神经元相连接,也就是我们所称的局部感知。表面上看局部连接似乎损失了部分信息,但实际上后层神经元并没有损失任何信息,只需要在更高层将局部的信息综合起来即可得到全局的信息。并且通过后面一层神经元感知局部信息不仅可以减少网络需要学习的大量参数,同时可以减少网络的冗余信息。
怕看不懂,稍微解释一下这个图(b),是由前一层的一个神经元在被卷积多次,在后一层的多个神经元中可能都有他的信息,如果这个图不太理解,那我们看个更直观的图。图来自这里。
这个图更为直观的指出了什么是局部感知,图中的红色绿色蓝色黑色的神经元都包含了前一层的部分信息,而后一层由很多这样的神经元构成,即前一层的神经元的信息一定存在于后一层的某一个神经元中,可能不只一个,后一层依旧包含了前一层的所有信息。
权值共享是卷积神经网络的另一个特性。在网络对输入图片进行卷积时,对于同一特征的提取,卷积核的参数是共享的,即卷积核中的参数是相同的。更直白的说,卷积神经网络中,权值共享是指在网络的不同位置使用相同的卷积核来提取特征。此外,权值共享还使得CNN具有平移不变性。也就是说,无论特征出现在图像的哪个位置,使用相同的卷积核都能够提取相似的特征,不会因为位置的变化而变化。上图解释:
 权值共享
权值共享 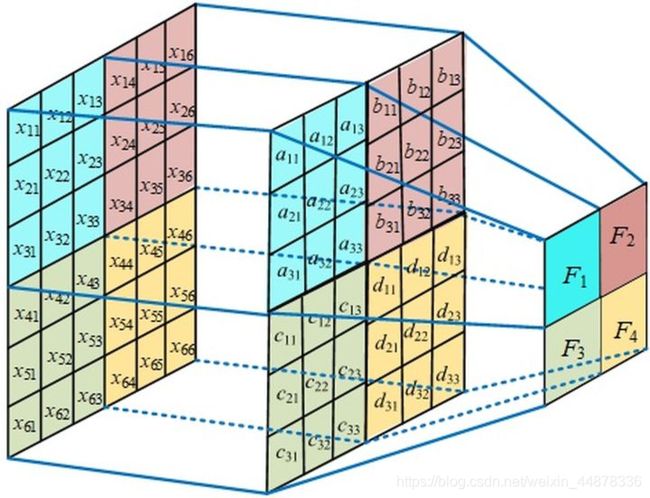 权值不共享
权值不共享
池化(子采样、降采样、汇聚)。会带来那些好处和坏处?
概念
首先解释一下,什么叫池化,池化又名子采样,汇聚,通过对输入的特征图进行某种统计操作(比如最大值、平均值等),将特征图划分为不重叠的区域,并对每个区域进行操作,从而得到一组新的特征图。简而改之,池化就是将输入图像的尺寸进行缩小,减少像素信息,只保留重要信息。
缩小图像(或称下采样,或称降采样),放大图像(或称上采样,或称图像插值)
汇聚层的主要作用是对卷积层输出的特征图进行下采样,通常有两种方式:最大池化(Max Pooling)和平均池化(Average Pooling)。
最大池化层的操作是在滑动窗口内寻找最大值作为该区域的输出.平均池化层的操作是在滑动窗口内计算均值作为该区域的输出
好处:
-
减少计算量:池化可以减小特征图的尺寸,能够有更低的维度,从而减少后续层级的计算量,提高计算效率。
-
参数共享:参数过多容易发生过拟合,由于池化不含可学习参数,因此池化操作并不会增加模型的参数数量,有利于减少过拟合的风险。
-
平移不变性:池化可以使特征对于位置的变化更加鲁棒,即使目标在图像中稍微移动,仍然可以检测到相同的特征。
潜在问题:
-
信息丢失:池化会舍弃部分细节信息,可能导致丢失对分类或者定位任务重要的细节。
-
分辨率下降:池化会导致特征图的尺寸减小,这可能会限制网络对输入数据细微变化的感知能力。
-
过度采样:在一些情况下,过度的池化操作可能会导致信息丢失过多,影响了网络对输入数据的有效表征。
全卷积网络
本段内容主要来自here
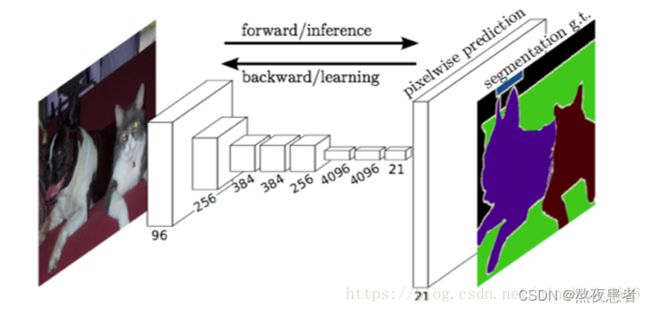
全卷积网络(Fully Convolutional Networks,FCN)将传统CNN后面的全连接层换成了卷积层,这样网络的输出将是热力图而非类别。同时,为解决卷积和池化导致图像尺寸的变小,使用上采样方式对图像尺寸进行恢复。
!!!并非去掉了池化,而是全连接
核心思想
- 不含全连接层的全卷积网络,可适应任意尺寸输入;
- 反卷积层增大图像尺寸,输出精细结果;
- 结合不同深度层结果的跳级结构,确保鲁棒性和精确性。
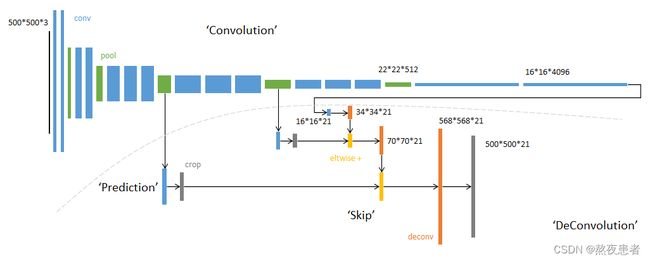
如图所示,FCN网络结构主要分为两个部分:全卷积部分和反卷积部分,其中全卷积部分为一些经典的CNN网络(如VGG,ResNet等),用于提取特征;反卷积部分则是通过上采样得到原尺寸的语义分割图像。FCN的输入可以为任意尺寸的彩色图像,输出与输入尺寸相同,通道数为n(目标类别数)+1(背景),结构如下:
低级特征、中级特征、高级特征
在计算机视觉领域和卷积神经网络中,低级特征、中级特征和高级特征是用于描述不同层次的图像特征表示的概念。
低级特征指的是在神经网络的浅层或较早的卷积层中提取到的原始、局部的图像特征。这些特征通常包含一些基本的形状、边缘、纹理和颜色等低层次的信息。
中级特征是在网络的中间层次进行提取的特征,它们具有比低级特征更高层次的抽象和语义含义。中级特征可以将低级特征组合起来,形成更具有代表性和抽象性的特征表示。
高级特征是在神经网络的较深层次中提取的抽象和语义丰富的特征表示。它们通过对中级特征的进一步组合和整合,能够对整体图像的语义信息和高层次结构进行建模。
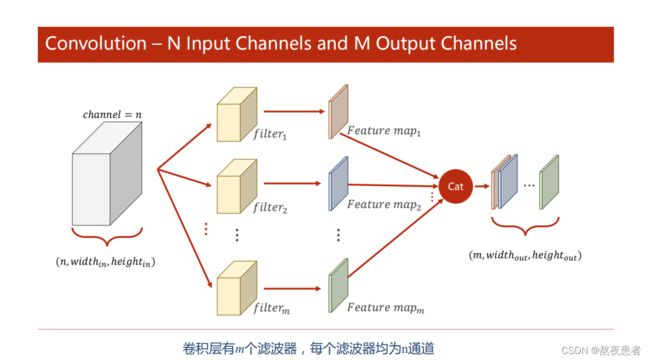
多通道。N输入,M输出是如何实现的?
首先遇事不决先放图,来源
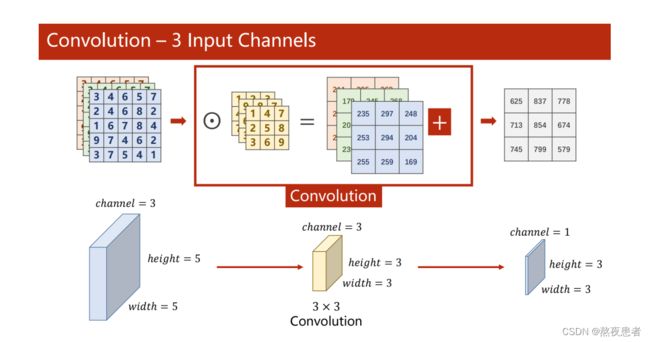
首先解释一下,通道的问题,对于输入图像当输入图像通道为n时,需要通道同样为n的卷积核组进行卷积,卷积后将n个通道相同位置上的点进行累加,最后输出为1通道的特征图.这就是多通道卷积的流程。那到底怎样输出的图像也是多通道呢?那就需要我们有多个卷积核组了,看下图:
简单解释一下图,首先输入图像的信息为![]() ,分别代表输入图像的通道,输入图像的宽、高,根据上面一个卷积核组对多通道输入的处理,我们知道一个卷积核组只能卷出来一个特征图,那为了获得多个通道的输出,所以需要多个卷积核组,将m个卷积核组卷积得到的特征图拼起来就是m个通道的多通道特征图。
,分别代表输入图像的通道,输入图像的宽、高,根据上面一个卷积核组对多通道输入的处理,我们知道一个卷积核组只能卷出来一个特征图,那为了获得多个通道的输出,所以需要多个卷积核组,将m个卷积核组卷积得到的特征图拼起来就是m个通道的多通道特征图。
有个疑问为什么一个卷积核组卷多通道的时候可以把得到的特征图压缩成一维,而这里多个卷积核组却不行?
这里解释一下这个操作的意义是什么,一个卷积核组可以理解为对一类特征进行提取,m个卷积核组是对m个不同的特征进行提取,因为我们卷积的操作就是为了提取特征,在对输入图像进行卷积的时候,输入的多个通道同时提取的是一个特征,所以压缩也不影响最后特征提取的结果,那如果把m个卷积核卷积的结果压缩的话,就不能体现每个卷积核组对图像的特征提取的结果,所以输入要保持多个通道的特征图,每一个特征图都是从原图像提取到不同的特征。
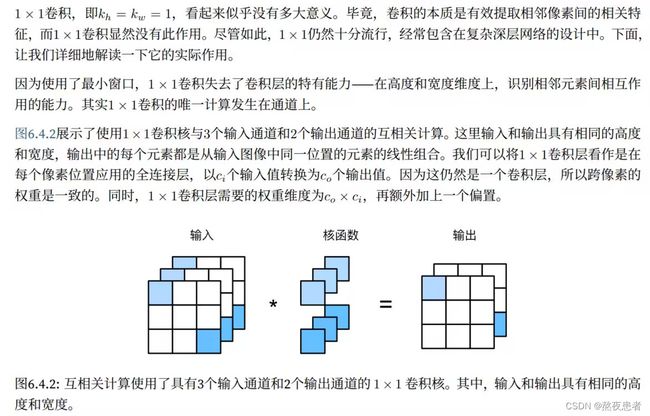
1×1的卷积核有什么作用
老师给的资料如下:
虚假的总结:1*1的卷积核就是为了改变输入输出的通道数量,不改变输入输出图像的高度和宽度。但是,学习要严谨,我觉得还不够,应该还有别的功能,通过资料搜素我们发现,1*1的卷积核具有4个作用,如下:
1、降维(减少参数)
2、升维(用最少的参数拓宽网络channal)
1、2两点博主是用数据各种模型举例,没看懂,等卷积神经网络学完了再回来改!链接放这儿难点
3、跨通道信息交互(channal 的变换)
这就是老师给的资料很好理解
4、增加非线性特性
可以在保持尺度不变的情况下增加非线性特征,利用1*1的卷积核后会通过激活函数。而激活函数具有增加非线性的作用。
二、使用CNN进行XO识别
1 复现资料中的代码
首先我先复刻了课上PPT的实现过程,总代码如下:
import numpy as np
import matplotlib.pyplot as plt
import torch.nn as nn
import torch
x = np.full((9, 9), -1.0)
for i in range(1, 8):
x[i][i] = 1.0
x[i][8 - i] = 1.0
x = torch.tensor(x, dtype=torch.float32).view([1, 1, 9, 9])
Kernel = [[], [], []]
Kernel[0] = torch.tensor([[1.0, -1.0, -1.0],
[-1.0, 1.0, -1.0],
[-1.0, -1.0, 1.0]], dtype=torch.float32).view([1, 1, 3, 3])
Kernel[1] = torch.tensor([[1, -1, 1],
[-1, 1, -1],
[1, -1, 1]], dtype=torch.float32).view([1, 1, 3, 3])
Kernel[2] = torch.tensor([[-1, -1, 1],
[-1, 1, -1],
[1, -1, -1]], dtype=torch.float32).view([1, 1, 3, 3])
torch.set_printoptions(precision=2)
def draw(draw_numpy, cmap):
# 显示热力图
plt.figure()
plt.imshow(draw_numpy, cmap=cmap, interpolation='nearest')
# 在图上添加数值显示
for i in range(draw_numpy.shape[0]):
for j in range(draw_numpy.shape[1]):
if draw_numpy[i][j] >= 0:
plt.text(j, i, f'{draw_numpy[i, j]:.2f}', ha='center', va='center', color='black')
else:
plt.text(j, i, f'{draw_numpy[i, j]:.2f}', ha='center', va='center', color='white')
plt.show()
def conv2d(input, Kernel, cmap="None"):
Conv = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, bias=False)
Conv.weight = torch.nn.Parameter(Kernel)
Conv_output = Conv(input) / 9
print(Conv_output)
Conv_output_picture = Conv_output.squeeze().cpu().detach().numpy()
if cmap != "None":
draw(Conv_output_picture, cmap)
return Conv_output
Conv1_output = conv2d(x, Kernel[0], 'Blues_r')
Conv2_output = conv2d(x, Kernel[1], 'Oranges_r')
Conv3_output = conv2d(x, Kernel[2], 'RdPu_r')
def max_pool(input, cmap="None"):
max_pool = nn.MaxPool2d(kernel_size=(2, 2), stride=2, ceil_mode=True)
max_pool_out = max_pool(input)
print(max_pool_out)
max_pool_out_picture = max_pool_out.squeeze().cpu().detach().numpy()
if cmap != "None":
draw(max_pool_out_picture, cmap)
return max_pool_out
max_pool1_out = max_pool(Conv1_output, 'Blues_r')
max_pool2_out = max_pool(Conv2_output, 'Reds')
max_pool3_out = max_pool(Conv3_output, 'RdPu_r')
def relu(intput, cmap="None"):
nn_relu = nn.ReLU()
relu_output = nn_relu(intput)
print(relu_output)
relu_output_picture = relu_output.squeeze().cpu().detach().numpy()
if cmap != "None":
draw(relu_output_picture, cmap)
return relu_output
relu_output1 = relu(Conv1_output, 'Blues_r')
relu_output2 = relu(Conv2_output, 'Reds')
relu_output3 = relu(Conv3_output, 'RdPu_r')
def train(input, Kernel, cmap):
conv1 = conv2d(input, Kernel)
relu1 = relu(conv1)
conv2 = conv2d(relu1, Kernel)
relu2 = relu(conv2)
max_pool1 = max_pool(relu2)
conv3 = conv2d(max_pool1, Kernel)
relu3 = relu(conv3)
max_pool2 = max_pool(relu3, cmap)
# train(x, Kernel[0], 'Blues_r')接下来对每一步骤进行详解
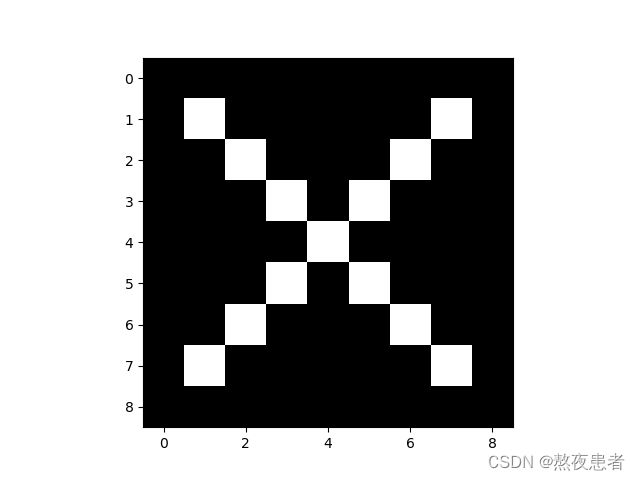
1.1 X图像的生成
x = np.full((9, 9), -1.0)
for i in range(1, 8):
x[i][i] = 1.0
x[i][8 - i] = 1.0
plt.imshow(x, cmap='gray')
x = torch.tensor(x, dtype=torch.float32).view([1, 1, 9, 9])
plt.show()代码的思路主要就是围绕首先生成一个9*9的值为-1的矩阵,通过修改斜线上的值,生成X的图像,并且将输入压为四维,为什么要是四维的数据,因为输入图像的格式为(N,C_in,H,W),详细介绍如下:
N——batch_size:一次训练所抓取的数据样本数量
C_in/C_out——输入图像的通道数:RGB\BGR图像这一维度就是3
H,W——对应的就是输入图像的高和宽
展示结果如下:
1.2 卷积核的初始化
Kernel = [[], [], []]
Kernel[0] = torch.tensor([[1.0, -1.0, -1.0],
[-1.0, 1.0, -1.0],
[-1.0, -1.0, 1.0]], dtype=torch.float32).view([1, 1, 3, 3])
Kernel[1] = torch.tensor([[1, -1, 1],
[-1, 1, -1],
[1, -1, 1]], dtype=torch.float32).view([1, 1, 3, 3])
Kernel[2] = torch.tensor([[-1, -1, 1],
[-1, 1, -1],
[1, -1, -1]], dtype=torch.float32).view([1, 1, 3, 3])view同样是压缩,将卷积核压缩为四维数据才能对卷积层的数据进行初始化,那卷积核压为的四维都是什么含义呢呢,卷积核四维可以如下:【out_channel, in_channel, H, W】,可以怎么理解呢,卷积核的四维分别为输入通道数量、输出通道数量、卷积核的高和宽,因为我们实验中,不同的卷积层通道数也不一样,所以,我用的这个方法并不适合实际应用,但是能明确卷积核的卷积原理。
重点!!!需要将卷积核的数据定义为float浮点类型,因为后来进行梯度下降的时候,必须是浮点数才可以!!!
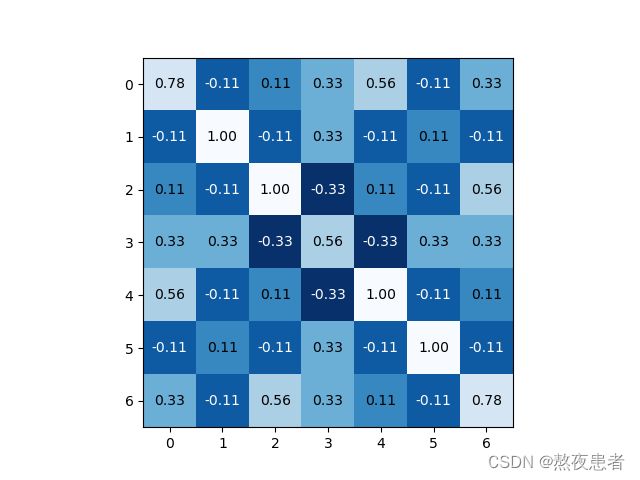
1.3 卷积
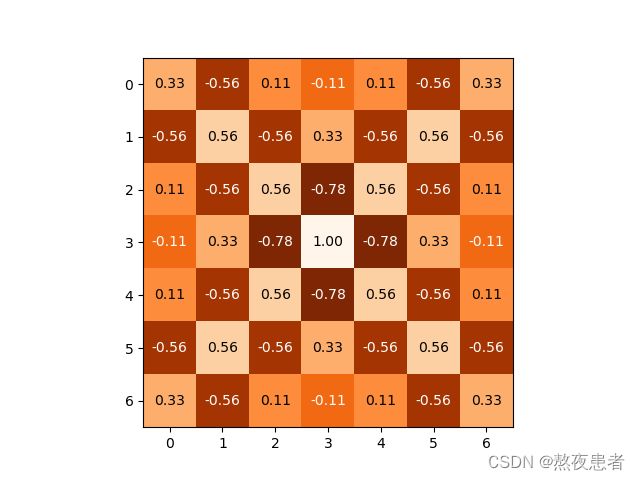
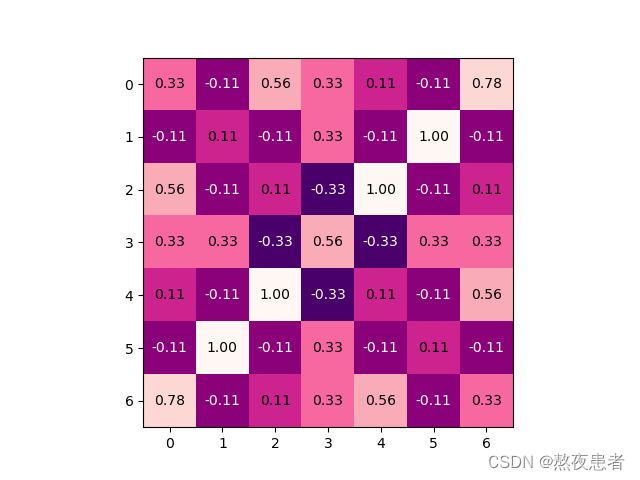
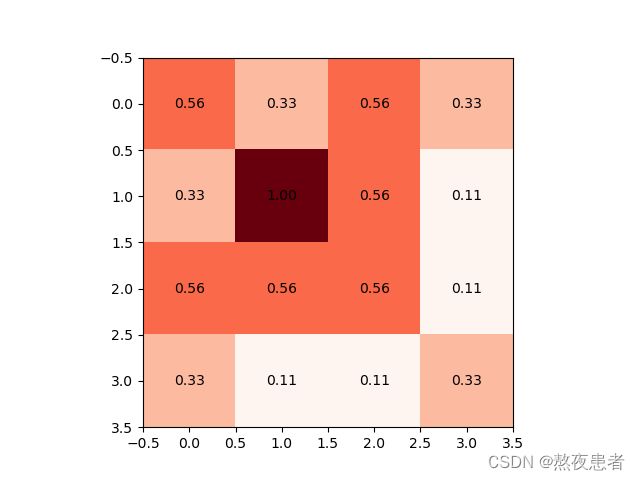
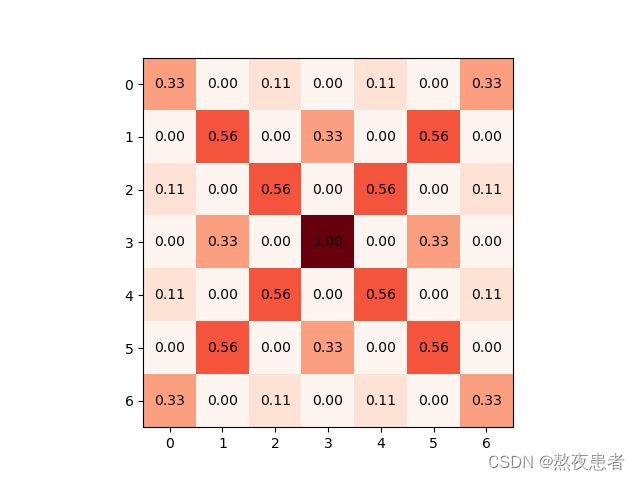
老师的材料中展示的卷积结果如下:
代码部分如下:
def conv2d(input, Kernel, cmap="None"):
Conv = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, bias=False)
Conv.weight = torch.nn.Parameter(Kernel)
Conv_output = Conv(input) / 9
print(Conv_output)
Conv_output_picture = Conv_output.squeeze().cpu().detach().numpy()
if cmap != "None":
draw(Conv_output_picture, cmap)
return Conv_output
Conv1_output = conv2d(x, Kernel[0], 'Blues_r')
Conv2_output = conv2d(x, Kernel[1], 'Oranges_r')
Conv3_output = conv2d(x, Kernel[2], 'RdPu_r')自己手写的卷积封装过程,input为待卷积的图像,Kernel为卷积核,我这里采用的卷积核初始化定义方法为torch.nn.Parameter方法,当然也可以直接复制法,代码如下:
Conv.weight.data = Kernel
结果都大差不差,nn.Conv2d为Pytorch提供的二维卷积函数,参数如下:
其他的参数都好理解,但是这个dilation到底是啥,空洞卷积是啥呢,通过老师发的资料,大体就可以理解。
1.3.1 空洞卷积
不理解?简单,我总结了一圈,大概只需要一句话来理解什么是空洞卷积:空洞卷积通过在卷积核中引入间距,使得卷积核在输入上以间隔进行采样,从而扩大了卷积核的感受野,但同时保持了参数数量的相对较少。过程如下图所示。
回到卷积层,卷积的展示结果如下:
较为完美的复刻,ppt展示的卷积采取的是小数点精确到两位,不四舍五入,我计算的采取四舍五入,所以会有0.01的误差,但是不影响观看。
1.4 池化
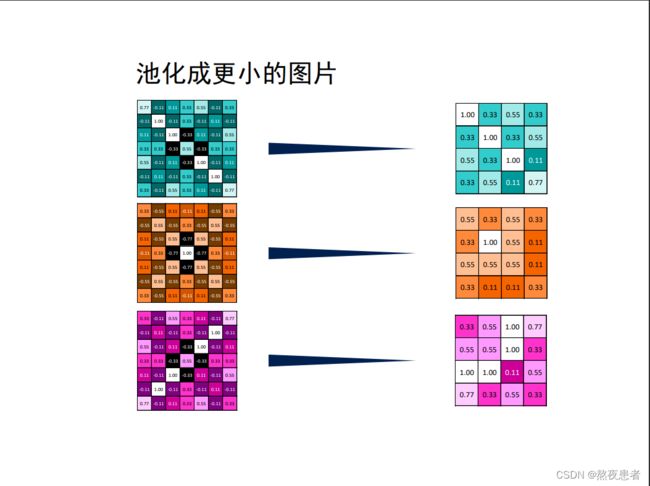
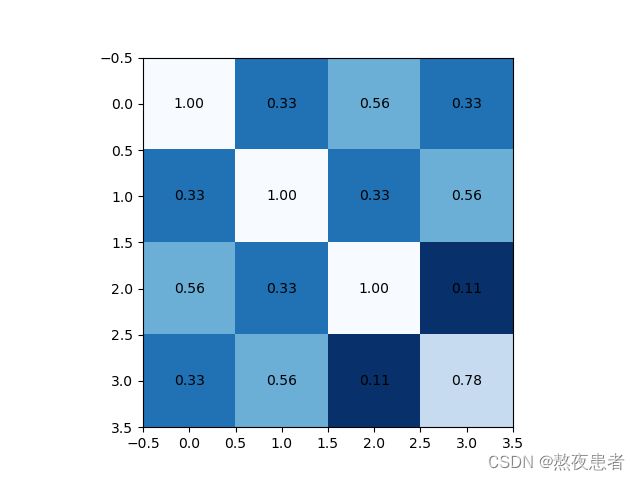
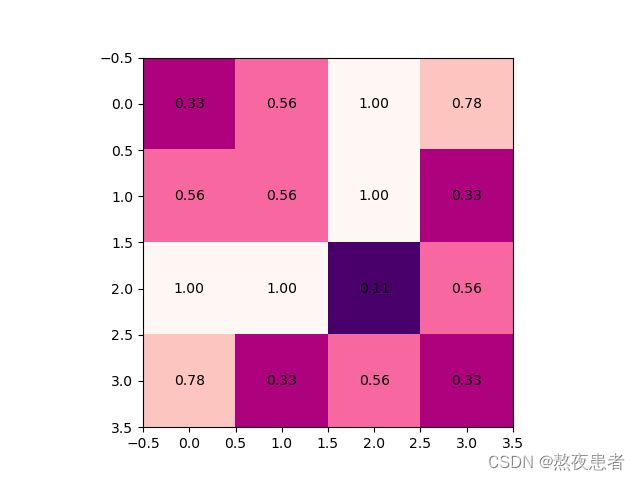
老师的材料中展示的池化结果如下:
代码部分如下:
def max_pool(input, cmap="None"):
max_pool = nn.MaxPool2d(kernel_size=(2, 2), stride=2, ceil_mode=True)
max_pool_out = max_pool(input)
print(max_pool_out)
max_pool_out_picture = max_pool_out.squeeze().cpu().detach().numpy()
if cmap != "None":
draw(max_pool_out_picture, cmap)
return max_pool_out
max_pool1_out = max_pool(Conv1_output, 'Blues_r')
max_pool2_out = max_pool(Conv2_output, 'Reds')
max_pool3_out = max_pool(Conv3_output, 'RdPu_r')input为待池化的输入图像,采用nn.MaxPool2d最大二维池化函数进行池化操作,具体的参数信息如下:
前四个参数都容易理解,最后两个参数一个是调整输出对象为最大值索引和输出,一个是调整向上还是向下取整。
池化的结果如下:
针对池化层,注意!!!这里展示的为向上取整,但是默认的都是向下取整,记得如果想向上取整的时候调整ceil_mode参数为True;
1.5 激活
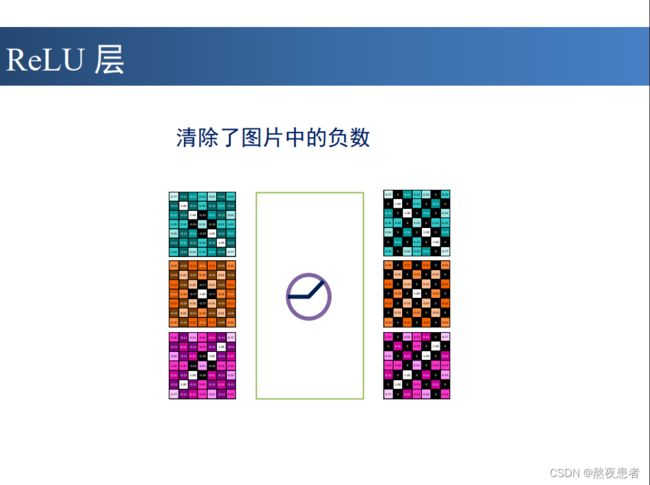
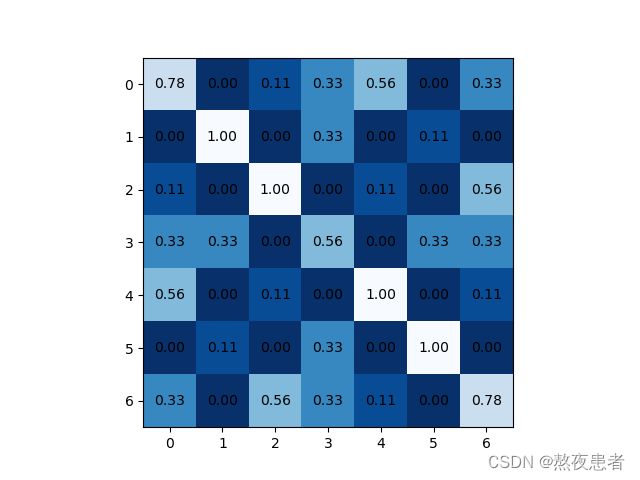
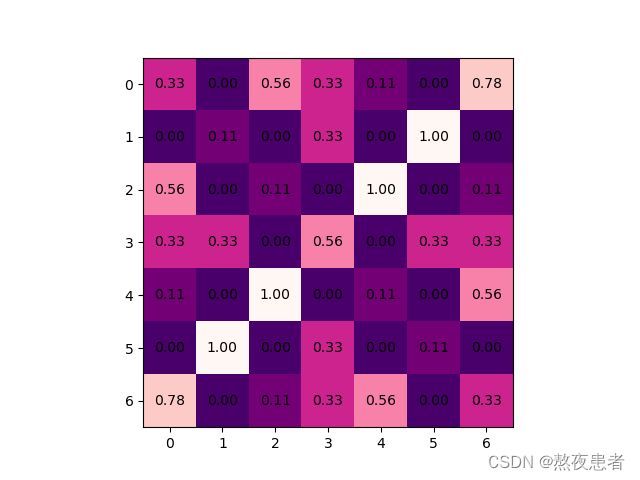
老师的材料中展示的池化结果如下:
代码部分如下:
def relu(intput, cmap="None"):
nn_relu = nn.ReLU()
relu_output = nn_relu(intput)
print(relu_output)
relu_output_picture = relu_output.squeeze().cpu().detach().numpy()
if cmap != "None":
draw(relu_output_picture, cmap)
return relu_output
relu_output1 = relu(Conv1_output, 'Blues_r')
relu_output2 = relu(Conv2_output, 'Reds')
relu_output3 = relu(Conv3_output, 'RdPu_r')这块就是老生长谈了,从线性规划,到前馈神经网络,再到现在的卷积这是我们唯一最熟悉的东西,所以这一块也是最为简单的这里不多做赘述了。
激活的结果如下:
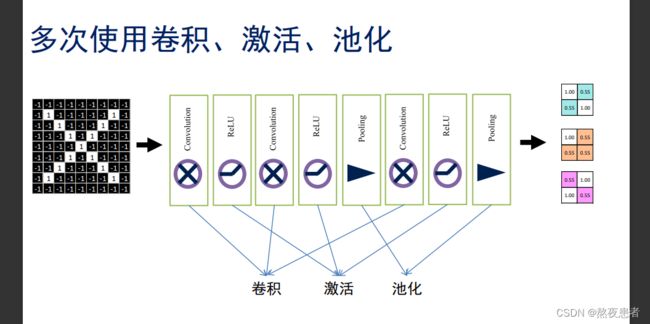
到这儿卷积老师PPT资料中的卷积神经网络已经复现完了,但是还是美中不足的,在最后集成的时候我发现不是想的那样,PPT展示的过程如下:
代码如下:
def train(input, Kernel, cmap):
conv1 = conv2d(input, Kernel)
relu1 = relu(conv1)
conv2 = conv2d(relu1, Kernel)
relu2 = relu(conv2)
max_pool1 = max_pool(relu2)
conv3 = conv2d(max_pool1, Kernel)
relu3 = relu(conv3)
max_pool2 = max_pool(relu3, cmap)
train(x, Kernel[0], 'Blues_r')这是我复现,卷积核1的卷积过程,但是最终报错,经过我推导发现好像最后的输出是1*1,这个输出4*4的特征图,到最后我也没想明白怎么出来的,等等同班其他同学有没有做的再回来修正吧
2、利用CNN对XO数据集进行训练+测试
下载好后的数据集,按照如下格式进行处理,分测试集和训练集。数据集中一共2000张图片,X、O各1000张。从X、O文件夹,分别取出150张作为测试集。
文件夹train_data:放置训练集 1700张图片
文件夹test_data: 放置测试集 300张图片
2.1 数据集
from torch.utils.data import DataLoader
from torchvision import transforms, datasets
# 将输入的图片先转换为灰度图,然后将其转换为 Tensor,并进行归一化处理。这样处理后的数据可以直接作为模型的输入。
transforms = transforms.Compose([
transforms.ToTensor(), # 把图片进行归一化,并把数据转换成Tensor类型
transforms.Grayscale(1) # 把图片 转为灰度图
])
# dataset.ImageFolder 将数据集封装为dataset类型
# root (string): 数据集的根目录路径。在这个根目录下,每个类别的图像应该被存放在一个单独的子文件夹中。每个子文件夹的名称将被视为一个类别,并且其中的图像将被标记为该类别。
# transform (callable, optional): 一个对图像进行变换的函数或转换操作。可以使用 transforms 模块中的函数来对图像进行预处理、数据增强等操作,例如将图像转换为 Tensor 类型、调整大小、裁剪等。
data_train = datasets.ImageFolder('train_data', transforms)
data_test = datasets.ImageFolder('test_data', transforms)
train_loader = DataLoader(data_train, batch_size=64, shuffle=True)
test_loader = DataLoader(data_test, batch_size=64, shuffle=True)
for i, data in enumerate(train_loader):
images, labels = data
print(images.shape)
print(labels.shape)
break
for i, data in enumerate(test_loader):
images, labels = data
print(images.shape)
print(labels.shape)
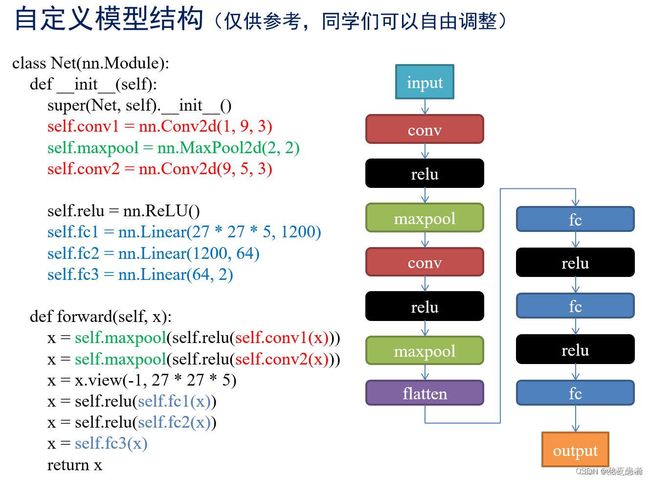
break2.2 模型构建
class CNN(nn.Module):
def __init__(self):
super(CNN, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=9, kernel_size=3)
self.pool = nn.MaxPool2d(kernel_size=2, stride=2)
self.conv2 = nn.Conv2d(in_channels=9, out_channels=5, kernel_size=3)
self.relu = nn.ReLU()
self.fc1 = nn.Linear(in_features=27 * 27 * 5, out_features=1200)
self.fc2 = nn.Linear(in_features=1200, out_features=64)
self.fc3 = nn.Linear(in_features=64, out_features=2)
def forward(self, input):
output = self.pool(self.relu(self.conv1(input)))
output = self.pool(self.relu(self.conv2(output)))
output = output.view(-1, 27 * 27 * 5)
output = self.relu(self.fc1(output))
output = self.relu(self.fc2(output))
output = self.fc3(output)
return output关于全连接层的展平操作
第一次卷积后size应该为116-3+1=114
第一次池化后size为114/2=57
第二次卷积size=57-3+1=55
第二次池化55/2=27.5
参照老师的代码这里选择默认下取整也就是27*27,但是也可以是28*28哈,如果是28*28记得将ceil_mode=True即可,然后修改线性全连接层的参数即可。结构图如下:
2.3 模型训练
model = CNN()
loss = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
epochs = 10
for epoch in range(epochs):
total_loss = 0.0
for i, data in enumerate(train_loader):
images, labels = data
out = model(images)
one_loss = loss(out, labels)
optimizer.zero_grad()
one_loss.backward()
optimizer.step()
total_loss += one_loss
if (i + 1) % 10 == 0:
print('[%d %5d] loss: %.3f' % (epoch + 1, i + 1, total_loss / 100))
total_loss = 0.0
print('train finish')
torch.save(model, 'model.pth') # 保存的是模型, 不止是w和b权重值
torch.save(model.state_dict(), 'model_name1.pth') # 保存的是w和b权重值2.4 模型测试
# 模型测试
import matplotlib.pyplot as plt
# 读取模型
model_load = torch.load('model.pth')
# 读取一张图片 images[0],测试
print("labels[0] truth:\t", labels[0])
x = images[0].unsqueeze(0)
predicted = torch.max(model_load(x), 1)
print("labels[0] predict:\t", predicted.indices)
img = images[0].data.squeeze().numpy() # 将输出转换为图片的格式
plt.imshow(img, cmap='gray')
plt.show()2.5 计算模型的准确率
model_load = torch.load('model.pth')
correct = 0
total = 0
with torch.no_grad(): # 进行评测的时候网络不更新梯度
for data in test_loader: # 读取测试集
images, labels = data
outputs = model_load(images)
_, predicted = torch.max(outputs.data, 1) # 取出 最大值的索引 作为 分类结果
total += labels.size(0) # labels 的长度
correct += (predicted == labels).sum().item() # 预测正确的数目
print('Accuracy of the network on the test images: %f %%' % (100. * correct / total))2.6 查看训练好的模型的特征图
# 看看每层的 卷积核 长相,特征图 长相
# 获取网络结构的特征矩阵并可视化
import torch
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
from torchvision import transforms, datasets
import torch.nn as nn
from torch.utils.data import DataLoader
# 定义图像预处理过程(要与网络模型训练过程中的预处理过程一致)
transforms = transforms.Compose([
transforms.ToTensor(), # 把图片进行归一化,并把数据转换成Tensor类型
transforms.Grayscale(1) # 把图片 转为灰度图
])
path = r'training_data_sm'
data_train = datasets.ImageFolder(path, transform=transforms)
data_loader = DataLoader(data_train, batch_size=64, shuffle=True)
for i, data in enumerate(data_loader):
images, labels = data
print(images.shape)
print(labels.shape)
break
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 9, 3) # in_channel , out_channel , kennel_size , stride
self.maxpool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(9, 5, 3) # in_channel , out_channel , kennel_size , stride
self.relu = nn.ReLU()
self.fc1 = nn.Linear(27 * 27 * 5, 1200) # full connect 1
self.fc2 = nn.Linear(1200, 64) # full connect 2
self.fc3 = nn.Linear(64, 2) # full connect 3
def forward(self, x):
outputs = []
x = self.conv1(x)
outputs.append(x)
x = self.relu(x)
outputs.append(x)
x = self.maxpool(x)
outputs.append(x)
x = self.conv2(x)
x = self.relu(x)
x = self.maxpool(x)
x = x.view(-1, 27 * 27 * 5)
x = self.relu(self.fc1(x))
x = self.relu(self.fc2(x))
x = self.fc3(x)
return outputs
# create model
model1 = Net()
# load model weights加载预训练权重
# model_weight_path ="./AlexNet.pth"
model_weight_path = "model_name1.pth"
model1.load_state_dict(torch.load(model_weight_path))
# 打印出模型的结构
print(model1)
x = images[0]
# forward正向传播过程
out_put = model1(x)
for feature_map in out_put:
# [N, C, H, W] -> [C, H, W] 维度变换
im = np.squeeze(feature_map.detach().numpy())
# [C, H, W] -> [H, W, C]
im = np.transpose(im, [1, 2, 0])
print(im.shape)
# show 9 feature maps
plt.figure()
for i in range(9):
ax = plt.subplot(3, 3, i + 1) # 参数意义:3:图片绘制行数,5:绘制图片列数,i+1:图的索引
# [H, W, C]
# 特征矩阵每一个channel对应的是一个二维的特征矩阵,就像灰度图像一样,channel=1
# plt.imshow(im[:, :, i])
plt.imshow(im[:, :, i], cmap='gray')
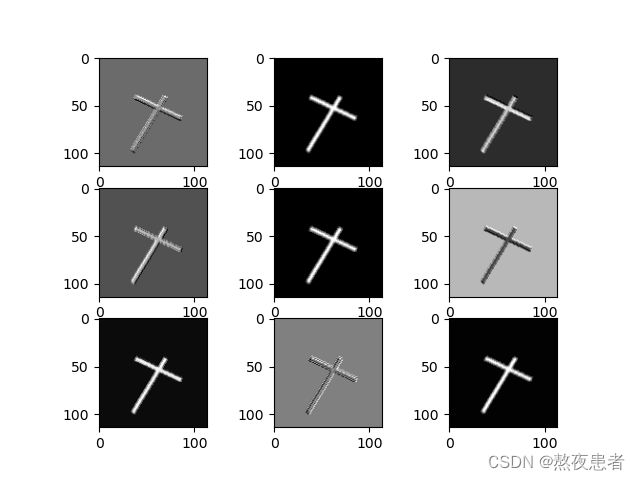
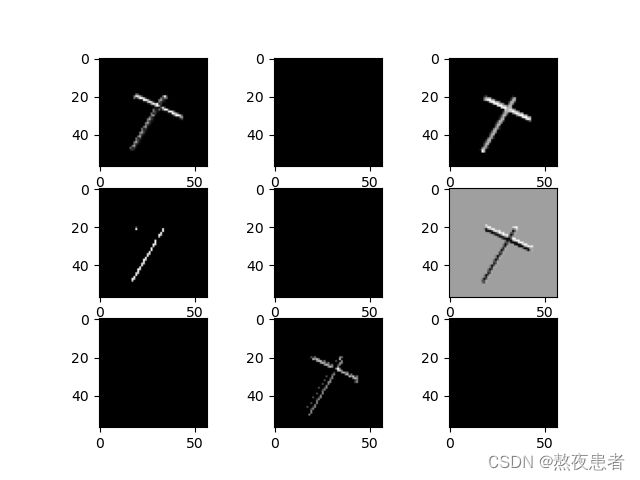
plt.show()卷积后的图像:
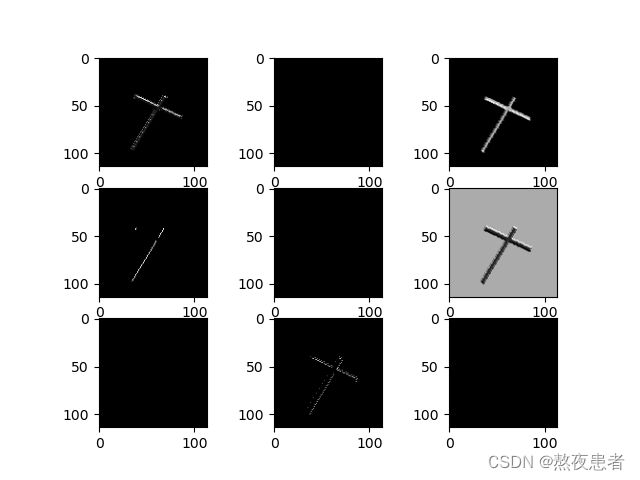
激活后的图像:
池化后的图像:
2.7 查看训练好的模型的卷积核
# 看看每层的 卷积核 长相,特征图 长相
# 获取网络结构的特征矩阵并可视化
import torch
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
from torchvision import transforms, datasets
import torch.nn as nn
from torch.utils.data import DataLoader
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 #有中文出现的情况,需要u'内容
# 定义图像预处理过程(要与网络模型训练过程中的预处理过程一致)
transforms = transforms.Compose([
transforms.ToTensor(), # 把图片进行归一化,并把数据转换成Tensor类型
transforms.Grayscale(1) # 把图片 转为灰度图
])
path = r'training_data_sm'
data_train = datasets.ImageFolder(path, transform=transforms)
data_loader = DataLoader(data_train, batch_size=64, shuffle=True)
for i, data in enumerate(data_loader):
images, labels = data
# print(images.shape)
# print(labels.shape)
break
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 9, 3) # in_channel , out_channel , kennel_size , stride
self.maxpool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(9, 5, 3) # in_channel , out_channel , kennel_size , stride
self.relu = nn.ReLU()
self.fc1 = nn.Linear(27 * 27 * 5, 1200) # full connect 1
self.fc2 = nn.Linear(1200, 64) # full connect 2
self.fc3 = nn.Linear(64, 2) # full connect 3
def forward(self, x):
outputs = []
x = self.maxpool(self.relu(self.conv1(x)))
# outputs.append(x)
x = self.maxpool(self.relu(self.conv2(x)))
outputs.append(x)
x = x.view(-1, 27 * 27 * 5)
x = self.relu(self.fc1(x))
x = self.relu(self.fc2(x))
x = self.fc3(x)
return outputs
# create model
model1 = Net()
# load model weights加载预训练权重
model_weight_path = "model_name1.pth"
model1.load_state_dict(torch.load(model_weight_path))
x = images[0]
# forward正向传播过程
out_put = model1(x)
weights_keys = model1.state_dict().keys()
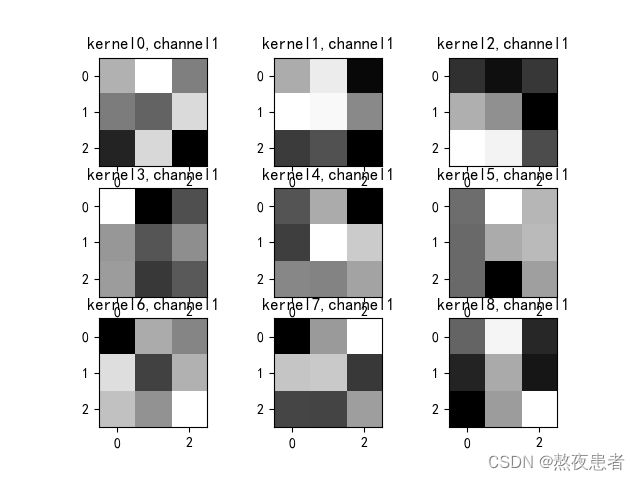
for key in weights_keys:
print("key :", key)
# 卷积核通道排列顺序 [kernel_number, kernel_channel, kernel_height, kernel_width]
if key == "conv1.weight":
weight_t = model1.state_dict()[key].numpy()
print("weight_t.shape", weight_t.shape)
k = weight_t[:, 0, :, :] # 获取第一个卷积核的信息参数
# show 9 kernel ,1 channel
plt.figure()
for i in range(9):
ax = plt.subplot(3, 3, i + 1) # 参数意义:3:图片绘制行数,5:绘制图片列数,i+1:图的索引
plt.imshow(k[i, :, :], cmap='gray')
title_name = 'kernel' + str(i) + ',channel1'
plt.title(title_name)
plt.show()
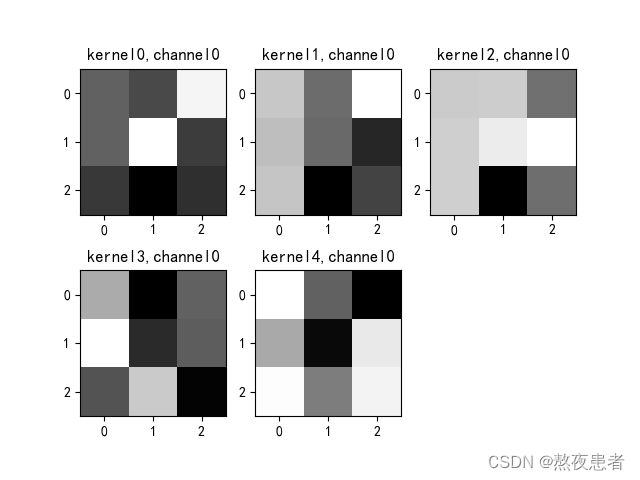
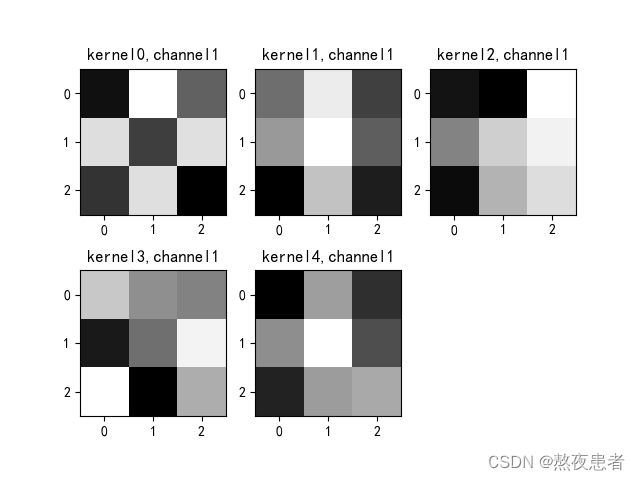
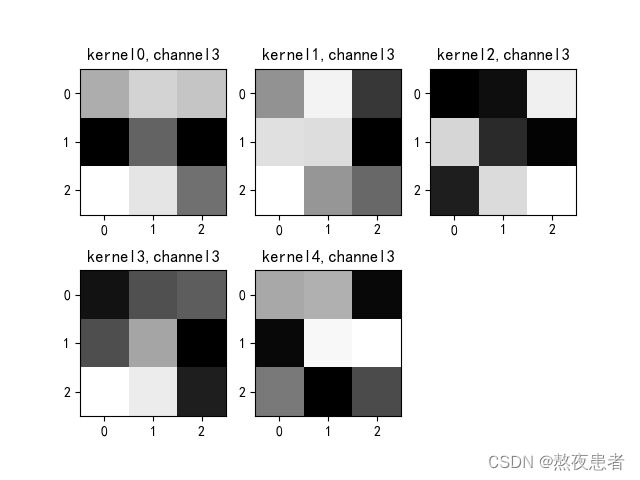
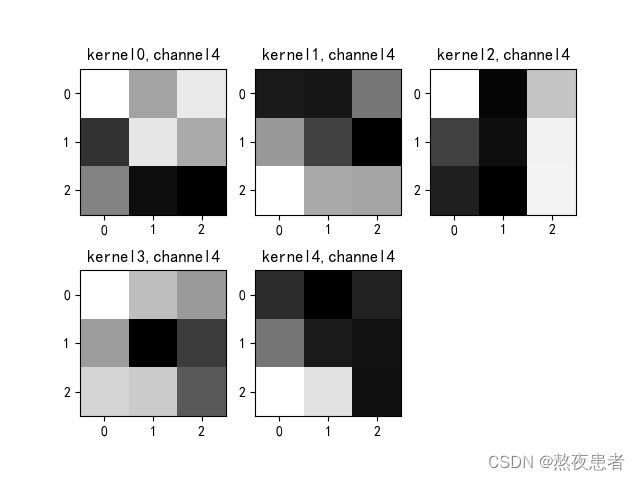
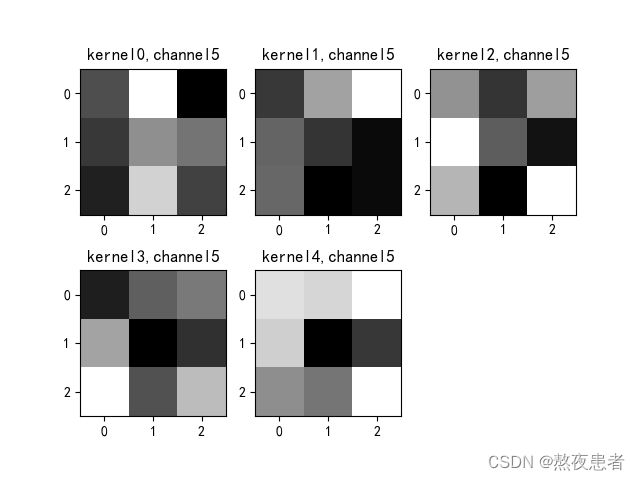
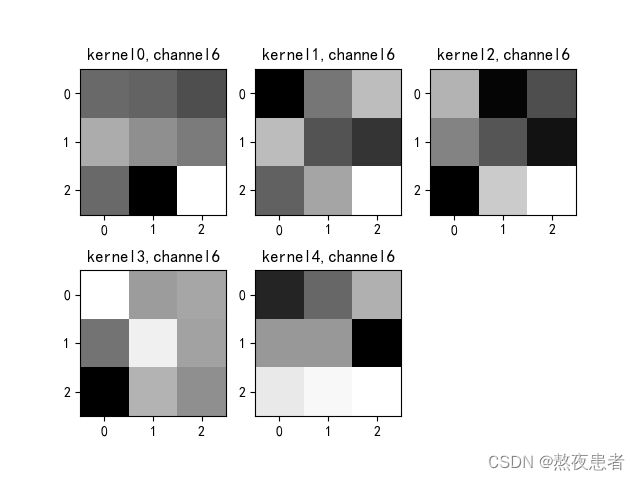
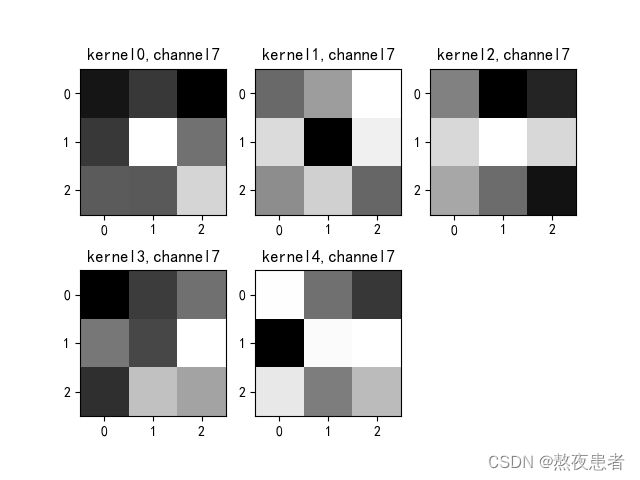
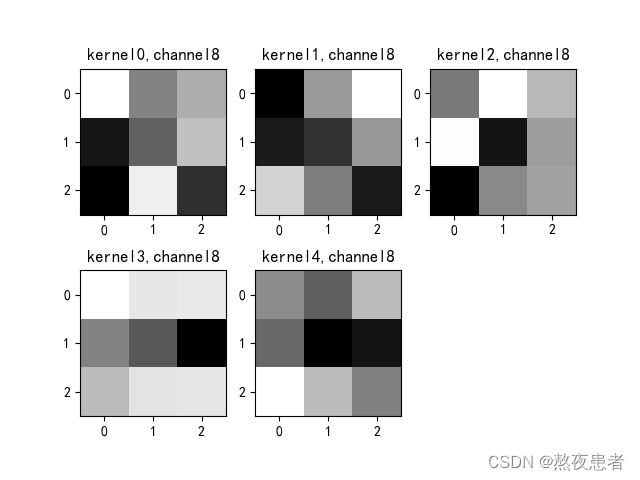
if key == "conv2.weight":
weight_t = model1.state_dict()[key].numpy()
print("weight_t.shape", weight_t.shape)
k = weight_t[:, :, :, :] # 获取第一个卷积核的信息参数
print(k.shape)
print(k)
plt.figure()
for c in range(9):
channel = k[:, c, :, :]
for i in range(5):
ax = plt.subplot(2, 3, i + 1) # 参数意义:3:图片绘制行数,5:绘制图片列数,i+1:图的索引
plt.imshow(channel[i, :, :], cmap='gray')
title_name = 'kernel' + str(i) + ',channel' + str(c)
plt.title(title_name)
plt.show()3 重新设计网络结构
首先回归刚刚卷积神经网络的正确率为93.33%,标记一下
3.1 至少增加一个卷积层,卷积层达到三层以上
代码如下:
import torch.nn as nn
import torch
from torch.utils.data import DataLoader
from torchvision import transforms, datasets
# 将输入的图片先转换为灰度图,然后将其转换为 Tensor,并进行归一化处理。这样处理后的数据可以直接作为模型的输入。
transforms = transforms.Compose([
transforms.ToTensor(), # 把图片进行归一化,并把数据转换成Tensor类型
transforms.Grayscale(1) # 把图片 转为灰度图
])
# dataset.ImageFolder 将数据集封装为dataset类型
# root (string): 数据集的根目录路径。在这个根目录下,每个类别的图像应该被存放在一个单独的子文件夹中。每个子文件夹的名称将被视为一个类别,并且其中的图像将被标记为该类别。
# transform (callable, optional): 一个对图像进行变换的函数或转换操作。可以使用 transforms 模块中的函数来对图像进行预处理、数据增强等操作,例如将图像转换为 Tensor 类型、调整大小、裁剪等。
data_train = datasets.ImageFolder('train_data', transforms)
data_test = datasets.ImageFolder('test_data', transforms)
train_loader = DataLoader(data_train, batch_size=64, shuffle=True)
test_loader = DataLoader(data_test, batch_size=64, shuffle=True)
for i, data in enumerate(train_loader):
images, labels = data
print(images.shape)
print(labels.shape)
break
for i, data in enumerate(test_loader):
images, labels = data
print(images.shape)
print(labels.shape)
break
class CNN(nn.Module):
def __init__(self):
super(CNN, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=9, kernel_size=3)
self.pool = nn.MaxPool2d(kernel_size=2, stride=2)
self.conv2 = nn.Conv2d(in_channels=9, out_channels=9, kernel_size=3)
self.conv3 = nn.Conv2d(in_channels=9, out_channels=5, kernel_size=3)
self.relu = nn.ReLU()
self.fc1 = nn.Linear(in_features=12 * 12 * 5, out_features=300)
self.fc2 = nn.Linear(in_features=300, out_features=64)
self.fc3 = nn.Linear(in_features=64, out_features=2)
def forward(self, input):
# 116 * 116
output = self.pool(self.relu(self.conv1(input)))
# 114 * 114 --> 57 * 57
output = self.pool(self.relu(self.conv2(output)))
# 57 * 57 --> 55 * 55 -- > 27 * 27
output = self.pool(self.relu(self.conv3(output)))
# 25 * 25 --> 12 * 12
output = output.view(-1, 12 * 12 * 5)
output = self.relu(self.fc1(output))
output = self.relu(self.fc2(output))
output = self.fc3(output)
return output
model = CNN()
loss = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
epochs = 30
for epoch in range(epochs):
total_loss = 0.0
for i, data in enumerate(train_loader):
images, labels = data
out = model(images)
one_loss = loss(out, labels)
optimizer.zero_grad()
one_loss.backward()
optimizer.step()
total_loss += one_loss
if (i + 1) % 10 == 0:
print('[%d %5d] loss: %.3f' % (epoch + 1, i + 1, total_loss / 100))
total_loss = 0.0
print('train finish')
torch.save(model, 'model.pth') # 保存的是模型, 不止是w和b权重值
torch.save(model.state_dict(), 'model_name1.pth') # 保存的是w和b权重值
correct = 0
total = 0
with torch.no_grad(): # 进行评测的时候网络不更新梯度
for data in test_loader: # 读取测试集
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, 1) # 取出 最大值的索引 作为 分类结果
total += labels.size(0) # labels 的长度
correct += (predicted == labels).sum().item() # 预测正确的数目
print('Accuracy of the network on the test images: %f %%' % (100. * correct / total))
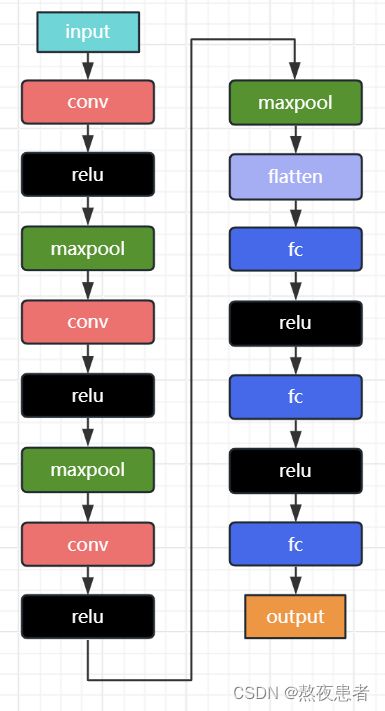
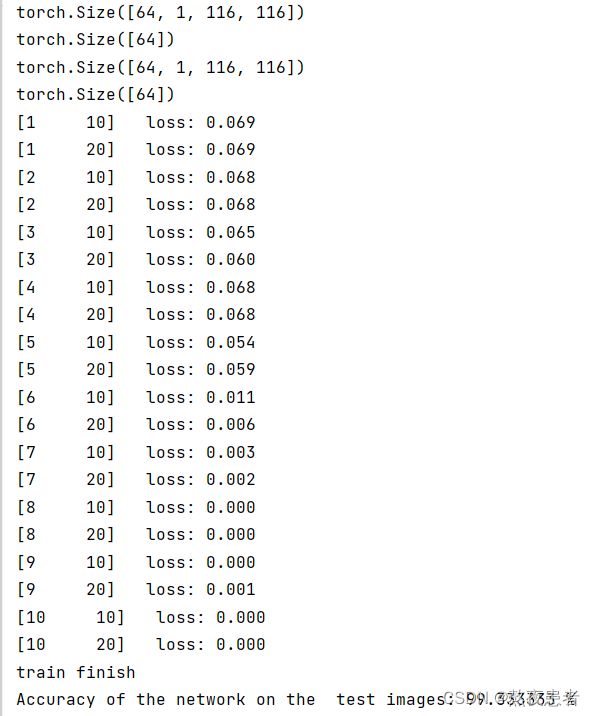
# 损失降低的很快,但是最后的时候收敛很慢这里我增加了一个卷积层,伴随而来增加了新的激活和池化过程,具体新的流程图如下:
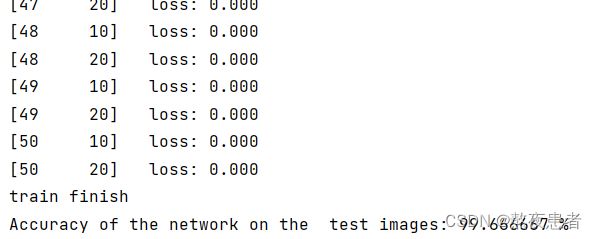
我们发现结果并不如人意,在相同的数据集增加一个卷积层结果反而变差,我怀疑是训练次数的问题,增加训练次数epoch=50,训练结果如下:
总结:增加卷积层性能增加,但是伴随而来的对于参数的学习也需要更多的训练次数,所以卷积神经网络也不能盲目的增加卷积层等来增加性能,伴随而来过多的训练次数也可能会增加过拟合的风险。
3.2 去掉池化层,对比“有无池化”的效果
代码如下:
import torch.nn as nn
import torch
from torch.utils.data import DataLoader
from torchvision import transforms, datasets
# 将输入的图片先转换为灰度图,然后将其转换为 Tensor,并进行归一化处理。这样处理后的数据可以直接作为模型的输入。
transforms = transforms.Compose([
transforms.ToTensor(), # 把图片进行归一化,并把数据转换成Tensor类型
transforms.Grayscale(1) # 把图片 转为灰度图
])
# dataset.ImageFolder 将数据集封装为dataset类型
# root (string): 数据集的根目录路径。在这个根目录下,每个类别的图像应该被存放在一个单独的子文件夹中。每个子文件夹的名称将被视为一个类别,并且其中的图像将被标记为该类别。
# transform (callable, optional): 一个对图像进行变换的函数或转换操作。可以使用 transforms 模块中的函数来对图像进行预处理、数据增强等操作,例如将图像转换为 Tensor 类型、调整大小、裁剪等。
data_train = datasets.ImageFolder('train_data', transforms)
data_test = datasets.ImageFolder('test_data', transforms)
train_loader = DataLoader(data_train, batch_size=64, shuffle=True)
test_loader = DataLoader(data_test, batch_size=64, shuffle=True)
for i, data in enumerate(train_loader):
images, labels = data
print(images.shape)
print(labels.shape)
break
for i, data in enumerate(test_loader):
images, labels = data
print(images.shape)
print(labels.shape)
break
class CNN(nn.Module):
def __init__(self):
super(CNN, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=9, kernel_size=3)
self.conv2 = nn.Conv2d(in_channels=9, out_channels=5, kernel_size=3)
self.relu = nn.ReLU()
self.fc1 = nn.Linear(in_features=112*112*5, out_features=1200)
self.fc2 = nn.Linear(in_features=1200, out_features=64)
self.fc3 = nn.Linear(in_features=64, out_features=2)
def forward(self, input):
output = self.relu(self.conv1(input))
output = self.relu(self.conv2(output))
output = output.view(-1, 112 * 112 * 5)
output = self.relu(self.fc1(output))
output = self.relu(self.fc2(output))
output = self.fc3(output)
return output
model = CNN()
loss = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
epochs = 10
for epoch in range(epochs):
total_loss = 0.0
for i, data in enumerate(train_loader):
images, labels = data
out = model(images)
one_loss = loss(out, labels)
optimizer.zero_grad()
one_loss.backward()
optimizer.step()
total_loss += one_loss
if (i + 1) % 10 == 0:
print('[%d %5d] loss: %.3f' % (epoch + 1, i + 1, total_loss / 100))
total_loss = 0.0
print('train finish')
torch.save(model, 'model.pth') # 保存的是模型, 不止是w和b权重值
torch.save(model.state_dict(), 'model_name1.pth') # 保存的是w和b权重值
correct = 0
total = 0
with torch.no_grad(): # 进行评测的时候网络不更新梯度
for data in test_loader: # 读取测试集
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, 1) # 取出 最大值的索引 作为 分类结果
total += labels.size(0) # labels 的长度
correct += (predicted == labels).sum().item() # 预测正确的数目
print('Accuracy of the network on the test images: %f %%' % (100. * correct / total))
# 损失降低的很快,但是最后的时候收敛很慢此时流程图为:
此时的结果为:
我们发现性能几乎不变,但是在实验过程中,明显发现因为没有池化层对图像的压缩处理,图片到全连接层依旧还有 112*112的大小,那么就依旧需要112*112*5的参数,相比于具有池化层,不仅大大减少了参数的数量,并且大大提升了运行的效率。所以池化还是很必要的。
3.3 修改“通道数”等超参数,观察变化
代码如下:
import torch.nn as nn
import torch
from torch.utils.data import DataLoader
from torchvision import transforms, datasets
# 将输入的图片先转换为灰度图,然后将其转换为 Tensor,并进行归一化处理。这样处理后的数据可以直接作为模型的输入。
transforms = transforms.Compose([
transforms.ToTensor(), # 把图片进行归一化,并把数据转换成Tensor类型
transforms.Grayscale(1) # 把图片 转为灰度图
])
# dataset.ImageFolder 将数据集封装为dataset类型
# root (string): 数据集的根目录路径。在这个根目录下,每个类别的图像应该被存放在一个单独的子文件夹中。每个子文件夹的名称将被视为一个类别,并且其中的图像将被标记为该类别。
# transform (callable, optional): 一个对图像进行变换的函数或转换操作。可以使用 transforms 模块中的函数来对图像进行预处理、数据增强等操作,例如将图像转换为 Tensor 类型、调整大小、裁剪等。
data_train = datasets.ImageFolder('train_data', transforms)
data_test = datasets.ImageFolder('test_data', transforms)
train_loader = DataLoader(data_train, batch_size=64, shuffle=True)
test_loader = DataLoader(data_test, batch_size=64, shuffle=True)
for i, data in enumerate(train_loader):
images, labels = data
print(images.shape)
print(labels.shape)
break
for i, data in enumerate(test_loader):
images, labels = data
print(images.shape)
print(labels.shape)
break
class CNN(nn.Module):
def __init__(self):
super(CNN, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=18, kernel_size=3)
self.pool = nn.MaxPool2d(kernel_size=2, stride=2)
self.conv2 = nn.Conv2d(in_channels=18, out_channels=5, kernel_size=3)
self.relu = nn.ReLU()
self.fc1 = nn.Linear(in_features=27 * 27 * 5, out_features=1200)
self.fc2 = nn.Linear(in_features=1200, out_features=64)
self.fc3 = nn.Linear(in_features=64, out_features=2)
def forward(self, input):
output = self.pool(self.relu(self.conv1(input)))
output = self.pool(self.relu(self.conv2(output)))
output = output.view(-1, 27 * 27 * 5)
output = self.relu(self.fc1(output))
output = self.relu(self.fc2(output))
output = self.fc3(output)
return output
model = CNN()
loss = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
epochs = 10
for epoch in range(epochs):
total_loss = 0.0
for i, data in enumerate(train_loader):
images, labels = data
out = model(images)
one_loss = loss(out, labels)
optimizer.zero_grad()
one_loss.backward()
optimizer.step()
total_loss += one_loss
if (i + 1) % 10 == 0:
print('[%d %5d] loss: %.3f' % (epoch + 1, i + 1, total_loss / 100))
total_loss = 0.0
print('train finish')
torch.save(model, 'model.pth') # 保存的是模型, 不止是w和b权重值
torch.save(model.state_dict(), 'model_name1.pth') # 保存的是w和b权重值
print('channel = 18')
correct = 0
total = 0
with torch.no_grad(): # 进行评测的时候网络不更新梯度
for data in test_loader: # 读取测试集
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, 1) # 取出 最大值的索引 作为 分类结果
total += labels.size(0) # labels 的长度
correct += (predicted == labels).sum().item() # 预测正确的数目
print('Accuracy of the network on the test images: %f %%' % (100. * correct / total))
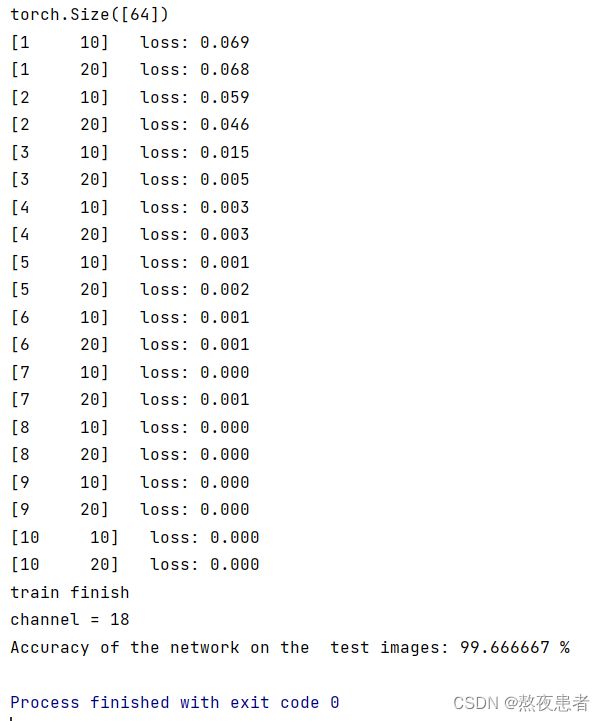
# 损失降低的很快,但是最后的时候收敛很慢本实验对模型的架构没发生影响,所以仅从时间效率和准确率的角度分析
我们发现性能有所提升,但是因为原本模型就已经具有良好的准确率了,这里表现不太明显,就时间效率而言,感受变化不大,但是理论上来说肯定是需要更多的时间的,准确率变化不明显那通道数变少呢呢,测试结果如下:
好叭,还是较好,到最后只能全部归结于,数据集太小2000数据不够卷积神经网络塞牙缝的。
4 可视化
其他实验内容都穿插在其他部分,这不就不复述一遍了。
探索低级特征、中级特征、高级特征
在卷积神经网络(CNN)中,不同层的卷积操作会捕获输入数据的不同特征。一般来说,随着网络层次的加深,卷积层捕获到的特征也逐渐变得更加抽象和高级。
通常情况下,浅层的卷积层(比如第一次卷积)会捕获到一些低级特征,例如边缘、纹理等;随着网络的加深,更深层的卷积层会逐渐捕获到更加抽象和语义化的特征,比如物体部件、图案、甚至是整体物体的特征。
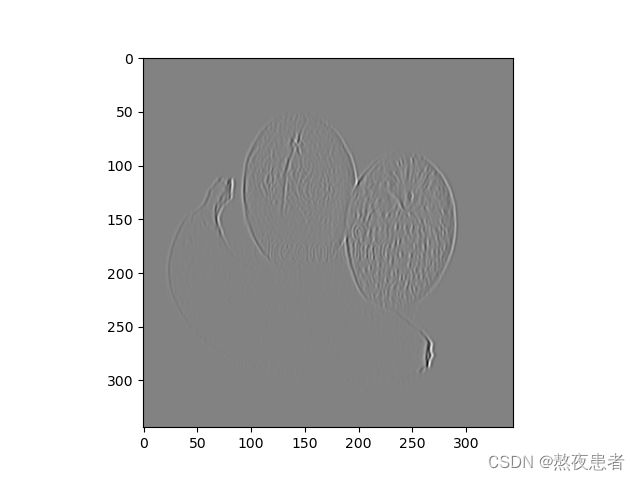
以此图为例提取,代码如下:
import os
import matplotlib.pyplot as plt
import torch
from PIL import Image
import numpy as np
import torch.nn as nn
def conv2d(input, Kernel):
plt.figure()
Conv = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, bias=False)
Conv.weight = torch.nn.Parameter(Kernel)
Conv_output = Conv(input)
Conv_output_picture = Conv_output.squeeze().cpu().detach().numpy()
plt.imshow(Conv_output_picture, cmap='gray')
plt.show()
return Conv_output
Kernel = torch.tensor([[1.0, -1.0, -1.0],
[2.0, 1.0, -2.0],
[1.0, -1.0, -1.0]], dtype=torch.float32).view([1, 1, 3, 3])
# 读取图片
img = Image.open('OrangeBananaApple.jpg')
img = img.convert('L')
print(img.size)
# 将图像转换为NumPy数组
img = img.resize((350, 350))
img_array = np.array(img)
x = torch.tensor(img_array, dtype=torch.float32).view([1, 1, 350, 350])
x_1 = conv2d(x, Kernel)
x_2 = conv2d(x_1, Kernel)
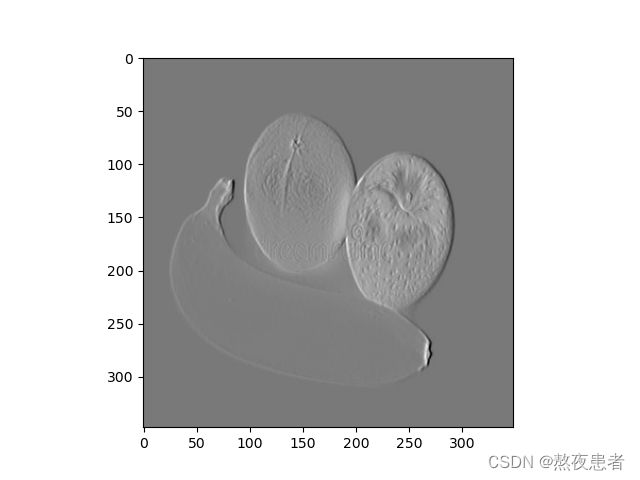
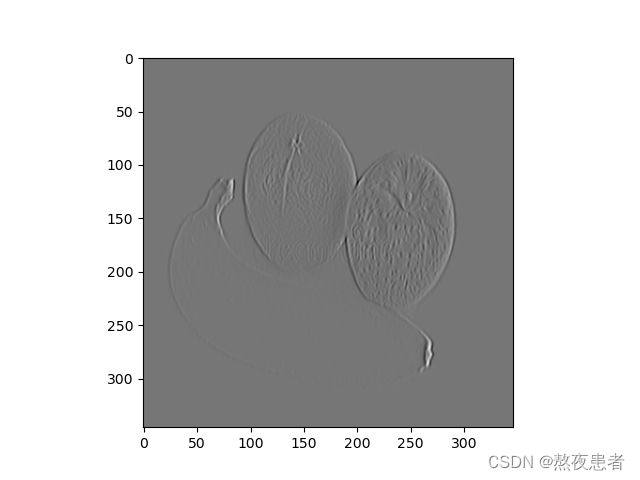
x_3 = conv2d(x_2, Kernel)我们假设第一次卷积的结果为低级特征,第二次卷积的结果为中级特征,第三次卷积的结果为高级特征,则对应的特征图为:
实验结果明显,,第一次卷积的结果为水果的边缘检验,是我们俗称的低级特征,第二次卷积我们能明显发现橘子表面的坑坑洼洼变得明显了,我们可以称之为中级特征,最后也就是最后一个图,我们发现对于橘子的花纹变得更加明显,我们称之为高级特征。
总结
本实验的收获真的很多,从最开始手动模拟PPT的卷积池化激活的过程,到从理论变成对数据集进行处理,对实战有了很大很大的提升,也花了很多的时间去分析老师的代码,学长们代码,皇天不负有心人,所得到收获也对得起自己付出的努力,接下来的目标对卷积神经网络这几个著名的模型VGG, AlexNet,都尝试着跑跑,加油!
附加:两个小问题,还没搞明白,等学完之后回来再解决!
关于DataLoader等对数据集的处理还是比较薄弱还是得加强,之前看到的一个很好很好的博客,放在这here
参考博客
局部感知与权值共享_局部感受野和权值共享_Le0v1n的博客-CSDN博客
卷积神经网络概述_什么是卷积神经网络-CSDN博客
池化的优点和缺点- CSDN搜索
FCN(全卷积神经网络)详解-菜鸟笔记 (coonote.com)
1×1 卷积核的作用_1*1卷积核有啥用-CSDN博客
【精选】NNDL 作业6:基于CNN的XO识别-CSDN博客
NNDL 作业6:基于CNN的XO识别_images.to('cuda')_笼子里的薛定谔的博客-CSDN博客
【23-24 秋学期】NNDL 作业7 基于CNN的XO识别-CSDN博客
【2021-2022 春学期】人工智能-作业6:CNN实现XO识别_x = self.conv2(x)#请问经过conv2(x)之后,x的维度是多少-CSDN博客