AIGC实战——变分自编码器(Variational Autoencoder, VAE)

0. 前言

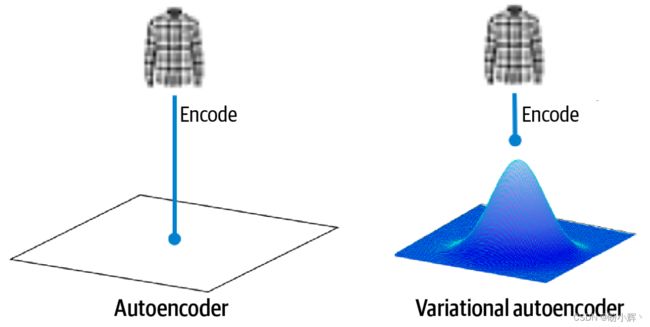
我们已经学习了如何实现自编码器，并了解了自编码器无法在潜空间中的空白位置处生成逼真的图像，且空间分布并不均匀，为了解决这些问题，我们需要将自编码器 (Autoencoder, AE) 改进为变分自编码器 (Variational Autoencoder, VAE)。在本节中，我们将学习变分自编码器的基本原理，并使用 Keras 实现变分自编码器模型。

1. 变分自编码器

1.1 基本原理

变分自编码器 (Variational Autoencoder, VAE) 是一种结合了自编码器和概率图模型的生成模型，通过学习输入数据的潜分布来进行无监督学习并生成新样本。
与传统的自编码器不同，变分自编码器引入了概率编码器和概率解码器。编码器将输入数据映射到潜在空间的概率分布，而解码器将从潜在空间中的样本重构为原始输入的分布。通过学习这两个概率分布，VAE 可以学习到输入数据的概率表示，并且能够通过从潜在空间中采样生成新的样本。
在训练过程中，VAE 使用最大似然估计来最小化观测数据与重构数据之间的差异，并通过最小化编码器和解码器之间的 KL 散度来约束潜在空间的分布与先验分布之间的差异。这使得 VAE 能够学习到连续且平滑的潜在表示，使得在潜在空间中的相邻点对应于语义上相似的样本。
接下来，我们从数学角度介绍我们需要哪些改动，才能将自编码器转换为变分自编码器，从而使其成为一个更复杂的生成模型。实际上，相比于自编码器，我们仅需要改变两部分：编码器和损失函数。

1.2 编码器

在自编码器中，每个图像直接映射为潜空间中的一个点。在变分自编码器中，每个图像映射为潜在空间中某一点周围的多元正态分布：

多元正态分布 (Multivariate Normal Distribution) 是一种概率分布，也称为高斯分布 (Gaussian Distribution)。其曲线图呈独特的钟形，一维的正态分布由两个变量确定：均值 ($\mu$) 和方差 (${\sigma }^2$)，标准差 ($\sigma$) 是方差的平方根。在一维空间中，正态分布的概率密度函数为：
$$f(x|\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$
下图展示了不同均值和方差的一维正态分布，红色曲线表示标准正态分布 (Standard Normal Distribution) $\mathcal{N}(0,1)$，即均值为 0，方差为 1 的正态分布。

可以使用以下公式从均值为 $\mu$，标准差为 $\sigma$ 的正态分布中采样一个点 $z$：
$$z=\mu +\sigma ϵ$$
其中 $ϵ$ 是从标准正态分布中采样得到的。
正态分布的概念可以扩展到多维空间，具有均值向量 $\mu$ 和对称协方差矩阵 $\Sigma$ 的 $k$ 维多元正态分布(或多元高斯分布) $\mathcal{N}(\mu ，\Sigma )$的概率密度函数如下：
$$f(x_1,...,x_k)=\frac{exp(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu ))}{\sqrt{(2\pi {)}^k|\Sigma |}}$$
我们通常使用各向同性的多元正态分布，其中协方差矩阵是对角矩阵。这意味着在每个维度上分布都是独立的，即我们可以采样一个向量，其中每个元素都服从独立的均值和方差的正态分布。
多元标准正态分布 (multivariate standard normal distribution) $\mathcal{N}(0,I)$ 是一个多元分布，具有零值均值向量和单位协方差矩阵。
在多数情况下，正态分布与高斯分布通常可以互换使用，并且通常隐含着各向同性和多元性。
变分自编码器假设潜空间中的维度之间没有相关性，因此协方差矩阵是对角矩阵。编码器只需将每个输入映射到一个均值向量和一个方差向量，而不需要考虑维度之间的协方差。
此外，我们选择映射为方差的对数，因为对数可以是 $(-\infty ,\infty )$ 范围内的任意实数，与神经网络单元的自然输出范围—致，而方差值始终为正。这样，我们可以使用神经网络作为编码器，将输入图像映射到均值和对数方差向量。
总之，编码器将每个输入图像编码为两个向量 z_mean 和 log_var，两者共同定义了潜空间中的多元正态分布：

• z_mean：分布的均值
• z_log_var：各个维度上方差的对数

我们可以使用以下公式从由上述值定义的分布中采样一个点 $z$：
$$z=z\_mean+z\_sigma\ast epsilon$$
其中：
$$\begin{gathered} z\_sigma=exp(z_{l}o{g}_{v}ar\ast 0.5) \\ epsilon\sim \mathcal{N}(0,I) \end{gathered}$$
$z\_sigma(\sigma )$ 和 $z\_log\_var(log({\sigma }^2))$ 之间的关系推导如下：
$$\sigma =exp(log(\sigma ))=exp(2log(\sigma )/2)=exp(log({\sigma }^2)/2)$$
变分自编码器的解码器与普通自编码器的解码器相同，整体结构如下所示：

为什么对编码器进行这样小的改变会有所帮助呢？在自编码器中，潜空间并不要求是连续的，即使点 (-2，2) 可以解码为完好的凉鞋图像，也不能保证点 (-2.1，2.1) 有类似的特征。而在变分自编码器中，由于我们从z_mean周围的区域中采样一个随机点，解码器必须确保当对同一邻域中的所有点进行解码时都能产生非常相似的图像，以便确保重构损失相对较小。这一属性确保了即使我们在隐空间中选择了一个解码器从未见过的点，编码器也可以将其解码为完好的图像。

2. 构建VAE编码器

接下来，我们利用 Keras 构建变分自编码器。

2.1 Sampling 层

首先，我们需要创建一种新层，称为 Sampling 层，用于从由 z_mean 和 z_log_var 定义的分布中采样：

# 通过继承 Keras 基础 Layer 类来创建一个新层
class Sampling(layers.Layer):
    def call(self, inputs):
        z_mean, z_log_var = inputs
        batch = tf.shape(z_mean)[0]
        dim = tf.shape(z_mean)[1]
        epsilon = K.random_normal(shape=(batch, dim))
        # 使用重参数化技巧构建一个从由 z_mean 和 z_log_var 参数化的正态分布中采样的样本
        return z_mean + tf.exp(0.5 * z_log_var) * epsilon

子类化 Layer 类
我们可以通过子类化 Layer 类并定义 call 方法在 Keras 中创建新的层，call 方法描述了如何通过该层转换张量。
例如，在变分自编码器中，可以创建一个 Sampling 层，处理从由 z_mean 和 z_log_var 定义的参数化正态分布中对 z 进行采样。子类化 Layer 类可以对一个张量应用不包含在 Keras 内置层类型中的变换。

重参数化技巧
变分自编码并不直接从由 z_mean 和 z_log_var 参数化的正态分布中进行采样，而是从标准正态分布中采样 epsilon，然后调整采样以得到正确的均值和方差，这称为重参数化技巧 (Reparameterization Trick)，使用此技术后，梯度可以自由地通过该层进行反向传播。通过将层的所有随机性都包含在变量 epsilon 中，可以证明该层输出相对于其输入的偏导数是确定性的(即与随机的 epsilon 无关)，这对于反向传播通过该层是至关重要的。

2.2 编码器

编码器的完整代码如下：

# 编码器
encoder_input = layers.Input(
    shape=(IMAGE_SIZE, IMAGE_SIZE, 1), name="encoder_input"
)
x = layers.Conv2D(32, (3, 3), strides=2, activation="relu", padding="same")(
    encoder_input
)
x = layers.Conv2D(64, (3, 3), strides=2, activation="relu", padding="same")(x)
x = layers.Conv2D(128, (3, 3), strides=2, activation="relu", padding="same")(x)
shape_before_flattening = K.int_shape(x)[1:]  

x = layers.Flatten()(x)
# 将 Flatten 层连接到 z_mean 和 z_log_var 层，而不是直接连接到 2D 潜空间中
z_mean = layers.Dense(EMBEDDING_DIM, name="z_mean")(x)
z_log_var = layers.Dense(EMBEDDING_DIM, name="z_log_var")(x)
# Sampling 层从由 z_mean 和 z_log_var 参数定义的正态分布中对潜空间中的点 z 进行采样
z = Sampling()([z_mean, z_log_var])
# 定义编码器，接受一张输入图像，并输出 z_mean、z_log_var 以及从由这些参数定义的正态分布中采样得到的点 z
encoder = models.Model(encoder_input, [z_mean, z_log_var, z], name="encoder")
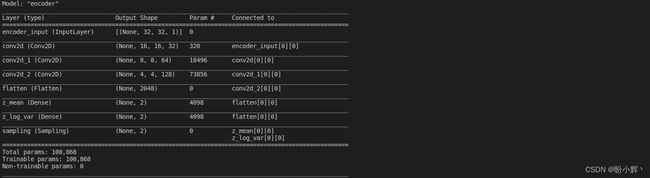
print(encoder.summary())

编码器架构摘要信息输出如下：

2.3 损失函数

在自编码器中，损失函数只包括经过编码器和解码器传递后的图像与其原始图像之间的重建损失。在变分自编码器中，除了重建损失外，还增加了一个额外的组成部分：KL 散度 (Kullback-Leibler divergence)。
KL 散度是衡量两个概率分布之间差异程度的方法。在 VAE 中，我们希望衡量由参数 z_mean 和 z_log_var 构成的正态分布与标准正态分布之间的差异程度。在这种情况下，可以证明 KL 散度有以下解析解：
$$kl\_loss=-0.5\ast sum(1+z\_log\_var-z\_mea{n}^2-exp(z\_log\_var))$$
用数学符号表示如下：
$$D_{KL}[\mathcal{N}(\mu ,\sigma )||\mathcal{N}(0,1)]=-\frac{1}{2}\sum (1+log({\sigma }^2)-{\mu }^2-{\sigma }^2)$$
求和是在潜空间的所有维度上进行的。当 z_mean = 0 且 z_log_var = 0 时，kl_loss 会得到最小值 0。当这两个项开始与 0 的差距增大时，kl_loss 也会随之增加。
总之，KL 散度在编码观测样本时，如果 z_mean 和 z_log_var 变量与标准正态分布参数(即 z_mean = 0 和 z_log_var = 0 )出现显著不同，对网络施加的惩罚。
在损失函数中添加 KL 散度后，就有一个明确定义的分布(即标准正态分布)，可以用于选择潜空间中的点，从该分布中采样更有可能得到 VAE 已经见过的范围内的点。其次，由于 KL 散度试图将所有编码分布强制趋近于标准正态分布，因此点簇之间形成较大间隙的可能性较小。相反，编码器将尝试以对称的方式高效利用原点周围的空白区域。
在 VAE 论文中，VAE 的损失函数只是重建损失和 KL 散度损失项之和。我们通过 r_loss_factor 为重建权重添加权重因子，用于平衡 KL 散度损失和重建损失。如果重建损失权重过大，KL 损失将无法产生预期的调节效果，就会遇到与普通自编码器相同的问题。如果 KL 散度项的权重过大，KL 散度损失将占主导地位，重建图像的质量将较差。权重因子是训练 VAE 时需要调整的超参数之一。

2.4 训练变分自编码器

将整个 VAE 模型构建为 Keras Model 类的子类，以便在自定义的 train_step 方法中计算损失函数的 KL 散度项。

class VAE(models.Model):
    def __init__(self, encoder, decoder, **kwargs):
        super(VAE, self).__init__(**kwargs)
        self.encoder = encoder
        self.decoder = decoder
        self.total_loss_tracker = metrics.Mean(name="total_loss")
        self.reconstruction_loss_tracker = metrics.Mean(
            name="reconstruction_loss"
        )
        self.kl_loss_tracker = metrics.Mean(name="kl_loss")

    @property
    def metrics(self):
        return [
            self.total_loss_tracker,
            self.reconstruction_loss_tracker,
            self.kl_loss_tracker,
        ]
    # 变分自编码器前向计算
    def call(self, inputs):
        """Call the model on a particular input."""
        z_mean, z_log_var, z = encoder(inputs)
        reconstruction = decoder(z)
        return z_mean, z_log_var, reconstruction
    # VAE训练过程，包括损失函数的计算
    def train_step(self, data):
        """Step run during training."""
        with tf.GradientTape() as tape:
            z_mean, z_log_var, reconstruction = self(data)
            reconstruction_loss = tf.reduce_mean(
                BETA
                * losses.binary_crossentropy(
                    data, reconstruction
                )
            )
            kl_loss = tf.reduce_mean(
                tf.reduce_sum(
                    -0.5
                    * (1 + z_log_var - tf.square(z_mean) - tf.exp(z_log_var)),
                    axis=1,
                )
            )
            total_loss = reconstruction_loss + kl_loss
        grads = tape.gradient(total_loss, self.trainable_weights)
        self.optimizer.apply_gradients(zip(grads, self.trainable_weights))
        self.total_loss_tracker.update_state(total_loss)
        self.reconstruction_loss_tracker.update_state(reconstruction_loss)
        self.kl_loss_tracker.update_state(kl_loss)

        return {m.name: m.result() for m in self.metrics}

    def test_step(self, data):
        """Step run during validation."""
        if isinstance(data, tuple):
            data = data[0]
        z_mean, z_log_var, reconstruction = self(data)
        # 重建损失权重因子 beta 为 500
        reconstruction_loss = tf.reduce_mean(
            BETA
            * losses.binary_crossentropy(data, reconstruction)
        )
        kl_loss = tf.reduce_mean(
            tf.reduce_sum(
                -0.5 * (1 + z_log_var - tf.square(z_mean) - tf.exp(z_log_var)),
                axis=1,
            )
        )
        # 总损失是重建损失和KL散度损失之和
        total_loss = reconstruction_loss + kl_loss

        return {
            "loss": total_loss,
            "reconstruction_loss": reconstruction_loss,
            "kl_loss": kl_loss,
        }

# 创建变分自编码器
vae = VAE(encoder, decoder)
# 编译变分自编码器
optimizer = optimizers.Adam(learning_rate=0.0005)
vae.compile(optimizer=optimizer)
# 模型训练
vae.fit(
    x_train,
    epochs=EPOCHS,
    batch_size=BATCH_SIZE,
    shuffle=True,
    validation_data=(x_test, x_test),
)

梯度记录器 (Gradient Tape)
TensorFlow 的 Gradient Tape 用于在模型的前向传播过程中计算操作的梯度。为了使用梯度记录器，需要将需要求导的操作的代码包装在 tf.GradientTape() 上下文中。一旦记录了这些操作，就可以通过调用 tape.gradient() 计算损失函数相对于某些变量的梯度，然后使用优化器利用这些梯度更新网络权重。
这一机制对于计算自定义损失函数的梯度非常有用，也适用于创建自定义的训练流程。

3. 变分自编码器分析

训练好 VAE 后，我们使用编码器对测试集中的图像进行编码，并在潜在空间中绘制 z_mean 值。我们还可以从标准正态分布中采样，生成潜空间中的点，并使用解码器将这些点解码回像素空间，以测试 VAE 的性能。
下图展示了新的潜空间的结构，以及采样点及其解码后的图像。我们可以看到潜空间的组织方式发生了 一些变化。

首先，KL 散度损失项确保编码图像的 z_mean 和 z_log_var 值不会偏离标准正态分布太远。其次，由于现在编码器是随机的而不是确定性的，因此，潜空间更加连续，所以不会生成过多不合理的图像，潜在空间现在更加连续。
最后，如下图所示，通过按图像类型对潜在空间中的点进行着色，可以看到没有任何一种类型有倾向性。右图显示了将潜空间转换为 p 值的情况，可以看到每种颜色占据的区域大致相等。需要强调的是，在训练过程中并没有使用标签，VAE 通过学习掌握了各种 Fashion-MNIST 图像的形式，以最小化重建损失。

小结

变分自编码器通过在模型中引入随机性，并限制潜空间中的点的分布来解决自编码器存在的问题。只需进行一些微小的调整，就可以将自编码器转换为变分自编码器，从而使其成为真正的生成模型。在本节中，我们介绍了变分自编码器的基本原理，并使用 Keras 实现了一个变分自编码器用于生成 Fashion-MNIST 图像。

系列链接

AIGC实战——生成模型简介
AIGC实战——深度学习 (Deep Learning, DL)
AIGC实战——卷积神经网络(Convolutional Neural Network, CNN)
AIGC实战——自编码器(Autoencoder)