Attention is all you need(Transformer)论文阅读笔记
一、背景
seq2seq模型(2014年):https://blog.csdn.net/zyk9916/article/details/118002934
Attention模型(2015年):https://blog.csdn.net/zyk9916/article/details/118498156
对于序列建模和转换问题,大量的研究都围绕以RNN为基础的encoder-decoder架构展开。
但是,RNN是一种时序模型,存在固有的顺序性。无论是在encoder还是decoder中,都需要获得上一个时刻的隐状态才能计算下一个时刻的隐状态。这严重阻碍了训练示例中的并行化。
本文提出了Transformer模型架构,它避免了递归和卷积,而是完全依赖于注意力机制来捕捉输入和输出之间的全局依赖关系。Transformer允许更大程度的并行化。
二、模型
Transformer模型遵循了之前的encoder-decoder架构。
Encoder:Encoder由N = 6个相同层的堆叠组成。每个层包含两个子层:一是多头自注意力机制(Multi-Head self-Attention),二是前馈神经网络(Feed Forward)。每个子层后都追加一个残差连接和归一化(Add&Norm)操作。模型中的所有子层以及Embedding层均产生维度dmodel = 512的输出。
Decoder:Decoder同样由N = 6个相同层的堆叠组成。每个层包含三个字层:一是带mask操作的多头自注意力机制(Masked Multi-Head self-Attention),二是Encoder到Decoder的多头注意力机制(注意这里并不是自注意力机制)(Encoder-Decoder Multi-Head Attention),三是前馈神经网络(Feed Forward)。每个子层同样追加一个残差连接和归一化(Add&Norm)操作。
2.2 注意力机制
注意力机制是基于三种向量(或者矩阵):查询向量(Query,Q)、键向量(Key,K)、值向量(Value,V)的信息选择机制。这里不进行详细介绍。
本节先介绍论文中用到的注意力机制,再详细说明他们是如何具体运用到模型中去的。
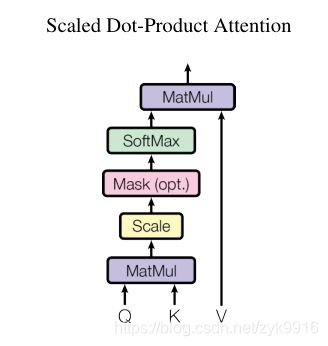
2.2.1 缩放点积注意力
给定dk维的查询向量和键向量,以及dv维的值向量作为输入,其计算出的注意力向量为:
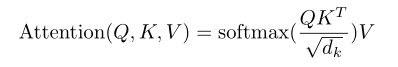
具体来说,注意力机制为句子中的每一个单词计算一个注意力向量Attention(Q,K,V),具体步骤为(这里设句子长度为seq_len):
用当前单词的Q向量与句子中所有单词的K向量计算

因为Q和K维度相同,得到seq_len个标量(这是一种打分机制),将它们输入softmax函数中计算分布(比例),再将每个比例乘以各自的V向量,最后相加,得到当前单词的注意力向量。
由于一个batch中,各个输入句子的长度可能不同,我们需要对输入序列进行对齐。即确定一个maxlength,在较短的序列后面填充 0。但是这些填充的位置其实并没有什么意义,不应当将注意力放在这些位置上,因此需要对Attention添加一个Mask机制。
具体的做法是,把这些位置的值加上一个相当大的负数,经过 softmax处理后,这些位置的概率就会趋近于0。
Attention向量计算示例:
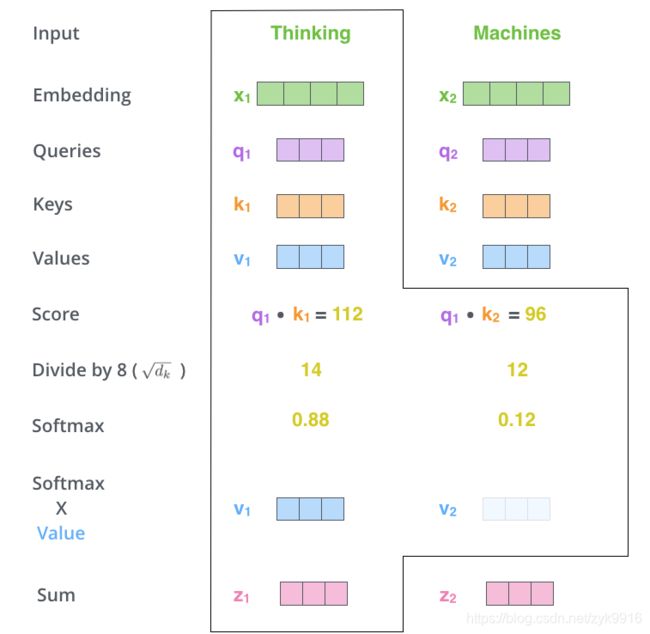
(图片来源:The Illustrated Transformer)
在Transformer中,每个词的注意力向量的计算是并行进行的(将Q,K,V作为矩阵运算)
2.2.2 多头注意力机制
简单来讲,就是讲上文提到的Q,K,V向量(或矩阵)通过多组(即多个头)线性变换矩阵(每组包括一个WiQ,WiK,WiV)映射成多个向量(或矩阵),再进行缩放点积的运算:

这里WiQ和WiK的维度为dmodel × dk,WiV维度为dmodel × dv。
计算出多个(h=8个)头的输出后,将结果连接,再经过一个线性变换矩阵Wo。Wo的维度为hdv × dmodel。
Transformer中设置dk = dv = dmodel/h = 64,以便各个层的输入维度保持一致。
2.2.3 Transformer中各种注意力机制的应用
① Encoder中的多头自注意力机制(Multi-Head self-Attention)
在自注意力机制中,Q = K = V = X ,X是上一个Encoder的输出(第一个Encoder的X是经过Embedding和Positional Encoding后的词向量)。经WiQ,WiK,WiV的线性变换后,得到三个新的查询向量,键向量,值向量,再进行注意力向量的计算。即:
headi = Attention(XWiQ,XWiK,XWiV)
② Decoder中的带mask操作的多头自注意力机制(Masked Multi-Head self-Attention)
与Encoder中的多头自注意力机制不同的是,Decoder中需要假如mask机制:
在传统的认知中,Decoder模型是将之前单词的表示作为输入,一个词一个词输出结果的,即当前单词的输出需要依赖于之前单词的输出。实际上,在训练过程中,Decoder也是可以并行执行的,这需要用到teacher force机制,即在每一轮预测时,不使用上一轮预测的输出,而强制使用训练数据的标准答案,即正确的单词(ground truth)。
比如将我爱你翻译为I love you,可能模型输出的第二个词为hate而非love,也仍然将I love的信息输入给Decoder。
这里可以参考https://zhuanlan.zhihu.com/p/166608727。
在此基础上,我们可以直接使用整个正确句子作为Decoder的输入。比如将我爱你翻译为I love you,在Decoder中使用 < bos > ,“I”,“love”,“you”,< eos> 作为输入。但是这样有一个问题,在Decoder预测“I”的时候,它只应该获得< bos>的信息,而不应该获得之后的词的信息。该如何解决这个问题呢?
答案是使用Mask机制。
我们将整个句子< bos > ,“I”,“love”,“you”,< eos> 作为输入,在进行注意力机制计算时,给超过当前词的部分赋予一个很大的负数值,这样在进行softmax计算时,其输出的权重接近于0,这样就屏蔽(mask)掉了后面的信息。
需要注意的是,teacher force机制只能在训练过程中使用,在测试过程中,还是要一个词一个词地串行计算。
③ Encoder到Decoder的多头注意力机制(Encoder-Decoder Multi-Head Attention)
注意这里不是自注意力机制了,Q,K,V分别来自不同的地方。
类似2015年的注意力模型,Q来自Decoder,K,V来自Encoder的输出(这里K=V)。
2.3 前馈神经网络(Feed Forward)
每个Encoder和Decoder层都包含一个全连接的前馈神经网络(但是不同层的参数是不同的),它包含了两个线性变换和一个ReLU激活:
![]()
前馈神经网络的输入和输出维度为dmodel = 512,中间层的维度为dff = 2048。
2.4 残差连接和归一化(Add&Norm)
残差连接:
假设在一个网络中,我们希望一个非线性单元f(x;θ)去逼近目标函数h(x)。可以将目标函数拆分为两部分:恒等函数x和残差函数h(x)-x。在实践中,残差函数比原始目标函数更容易学习。因此可以将原来的优化问题转变为:让非线性单元f(x;θ)去逼近残差函数h(x)-x,即用f(x;θ)+x逼近h(x)。
应用到Transformer 中,Encoder和Decoder中每个层的每个子层的输出为:
LayerNorm(x + Sublayer(x))。LayerNorm表示层归一化。
层归一化:
即对一个中间层的所有神经元进行归一化,与batch无关。
2.5 Embedding和Positional Encoding
Embedding不再赘述,即像大部分词向量模型一样,将word映射为dmodel维的向量。
Positional Encoding:
由于Transformer完全依赖于注意力机制,而不使用RNN的结构,就缺少了词在句子中的位置信息。论文中采用正弦和余弦函数来赋予词位置信息:
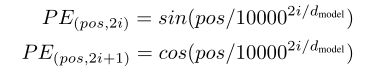
其中pos是词在句子中的位置,i是当前计算的维度是Embedding中的第几个维度(共512维)。
计算出每个词的Positional Encoding后,将其与Embedding相加即可。
2.6 Linear和Softmax
Decoder输出结果后,需要经过一个Linear层和Softmax层计算概率。
Linear层的输出维度为词表的大小,Softmax计算每个词的概率,最后输出概率最大的词,并计算损失。