LeetCode——数组（Java）

简介

记录一下自己刷题的历程以及代码。写题过程中参考了 代码随想录。会附上一些个人的思路，如果有错误，可以在评论区提醒一下。

二分查找

数组——二分查找

移除元素

一旦设计到数组移除元素，就可以首先考虑一下双指针法解题。
双指针中的快慢指针法经常可以比较高效的对数组做一遍处理，把需要删除的元素删掉进行压缩。

[简单] 27. 移除元素

原题链接

（注意：这样的方法是一种不保留原先顺序的方法）
方法①：其实也是一种双指针的思路。设置一个下标指向数组最右边，从头开始遍历，一旦遍历到有元素需要移除，就把他往最后放，并将下标左移，右边区域不再参与遍历，记住一旦有元素被置换到后面，需要将当前循环下标做i--处理，因为你换过来的元素依然可能是一个需要移除的元素。

class Solution {
    public int removeElement(int[] nums, int val) {
        int length = nums.length;
        int right = nums.length - 1; //替换指针
        for(int i = 0; i < length; i++){
            if(nums[i] == val){
                int temp = nums[right];
                nums[right] = nums[i];
                nums[i] = temp;
                right--;
                length--;  //相当于舍弃末尾的部分长度
                i--; //置换之后当前位置可能还是一个需要置换的元素，继续检查
            }
        }
        return length;
    }
}

（注意：该方法保留了原数组的顺序）
方法②：快慢指针法，相当于慢指针负责对快指针指向的元素进行复制，而快指针则会跳过那些不需要复制的元素。

class Solution {
    public int removeElement(int[] nums, int val) {
        int fastIndex = 0;
        int slowIndex = 0;
        int count = 0;
        while(fastIndex < nums.length && slowIndex < nums.length - count){
            nums[slowIndex] = nums[fastIndex];
            if(nums[fastIndex] == val){
                count++; 
            }else{
                slowIndex++;
            }
            fastIndex++;
        }
        return nums.length - count;
    }
}

[简单] 26. 删除有序数组中的重复项

原题链接

方法①：根据有序数组的条件，对上面的双指针法进行一定的改造，定义一个tag标记目前碰到的数，之后碰到相同的则快指针跳过，碰到不同的则标记新的tag。

class Solution {
    public int removeDuplicates(int[] nums) {  
        int fastIndex = 1;
        int slowIndex = 1;
        int count = 0;
        int tag = nums[1];  //题目为有序数组
        while(fastIndex < nums.length && slowIndex < nums.length - count){
            nums[slowIndex] = nums[fastIndex];
            if(nums[fastIndex] == tag){
                count++;
            }else{
                tag = nums[fastIndex];
                slowIndex++;
            }
            fastIndex++;
        }
        return nums.length - count;
    }
}

方法②：直接省去标记的问题，因为数组是有序的，慢指针和快指针所指向的元素只有nums[fastIndex] > nums[slowIndex]以及nums[fastIndex] == nums[slowIndex]两种情况，相等的时候快指针即可跳过，一旦不相等即可做赋值操作。

public int removeDuplicates(int[] nums) {
        //题目为有序数组
        int fastIndex = 0;
        int slowIndex = 0;
        while(fastIndex < nums.length){
            if(nums[fastIndex] > nums[slowIndex]){
                nums[++slowIndex] = nums[fastIndex];
            }else{
                fastIndex++;
            }
        }
        return slowIndex + 1;
    }

方法①与方法②速度差距：

[简单] 283. 移动零

原题链接

经典的双指针法。因为末尾要保留0，所以使用对换的swap方式来做。但这样时间效率不是最高的，直接覆盖，然后在末尾使用Arrays.fill(nums,count,nums.length,0);直接填充0能够更高效。

class Solution {
    public void moveZeroes(int[] nums) {
        int fastIndex = 0;
        int slowIndex = 0;
        while(fastIndex < nums.length){
            if(nums[fastIndex] != 0){
                int temp = nums[fastIndex];
                nums[fastIndex] = nums[slowIndex];
                nums[slowIndex] = temp;
                slowIndex++;
            }
            fastIndex++;
        }
    }
}

[简单] 844. 比较含退格的字符串

原题链接

方法①：也可以用快慢指针法，把两个字符串该删的删了对最后的结果作比较，这里就不重复实现了。

方法②：看到退格操作'#'就想到使用栈，用两个栈保存s和t经过退格操作之后的值，然后再出栈进行比较。

class Solution {
    public boolean backspaceCompare(String s, String t) {
        Stack<Character> sStack = new Stack<>();
        Stack<Character> tStack = new Stack<>();
        for(int i = 0; i < s.length(); i++){
            if(s.charAt(i) == '#' && !sStack.empty()){
                sStack.pop();
            }else if(s.charAt(i) != '#'){
                sStack.push(s.charAt(i));
            }
            //System.out.println(sStack.toString());
        }
        for(int i = 0; i < t.length(); i++){
            if(t.charAt(i) == '#' && !tStack.empty()){
                tStack.pop();
            }else if(t.charAt(i) != '#'){
                tStack.push(t.charAt(i));
            }
            //System.out.println(tStack.toString());
        }
        if(sStack.size() != tStack.size()) return false;
        while(!sStack.empty() && !tStack.empty()){
            if(sStack.pop() != tStack.pop()) return false;
        }
        return true;
    }
}

方法③：两个指针从后往前遍历，效率高，但是对边界的控制比较麻烦，没有栈写起来简单

class Solution {
    public boolean backspaceCompare(String s, String t) {
        int sIndex = s.length() - 1;
        int tIndex = t.length() - 1;
        int sCount = 0;
        int tCount = 0;
        while(sIndex >= 0 || tIndex >= 0){
            //让sIndex指向s中接下来要比较的字符（能够确定最后不被删除
            while (sIndex >= 0){
                if (s.charAt(sIndex) == '#') {
                    sCount++;
                    sIndex--;
                } else if (sCount > 0) {
                    sCount--;
                    sIndex--;
                } else{
                    break;
                }
            }
            while (tIndex >= 0){
                if (t.charAt(tIndex) == '#') {
                    tCount++;
                    tIndex--;
                } else if (tCount > 0) {
                    tCount--;
                    tIndex--;
                } else{
                    break;
                }
            }
            if(sIndex < 0 || tIndex < 0) break;
            if (s.charAt(sIndex) != t.charAt(tIndex)){
                return false;
            }
            sIndex--;
            tIndex--;
        }
        if(sIndex >=0 || tIndex >= 0) return false;
        return true;
    }
}

[简单] 977. 有序数组的平方

原题链接

题目中没有强调在原数组上修改，返回值也是int[]，就可以思考是不是创建一个新的数组更方便一些。
找到数组中正负值的分界点，然后从分界点向两边遍历，按照绝对值的大小挨个平方计算后加入到新的数组中。正数或者负数用完之后无法继续进行绝对值比较的循环。然后再将左边或者右边剩下的数依次放入答案数组中。
时间复杂度O(n)

class Solution {
    public int[] sortedSquares(int[] nums) {
        int[] answer = new int[nums.length];
        int zeroIndex = 0;
        //找到正负分界点
        while(zeroIndex < nums.length && nums[zeroIndex] < 0){
            zeroIndex++;
        }
        int negativeIndex = zeroIndex - 1;
        int positiveIndex = zeroIndex;
        int i = 0;
        while(negativeIndex >= 0 && positiveIndex < nums.length){
            if (Math.abs(nums[negativeIndex]) < Math.abs(nums[positiveIndex])) {
                answer[i++] = nums[negativeIndex] * nums[negativeIndex];
                negativeIndex--;
                continue;
            } else {
                answer[i++] = nums[positiveIndex] * nums[positiveIndex];
                positiveIndex++;
                continue;
            }
        }
        while(negativeIndex >= 0){
            answer[i++] = nums[negativeIndex] * nums[negativeIndex];
            negativeIndex--;
        }
        while(positiveIndex < nums.length){
            answer[i++] = nums[positiveIndex] * nums[positiveIndex];
            positiveIndex++;
        }
        return answer;
    }
}

[中等] 209.长度最小的子数组

原题链接

还是类似双指针的思路：滑动窗口
最朴素的思路就是二重循环，二重循环中一般第一重循环找起始点i，第二重循环找结束点j，判断i到j相加的所有情况。滑动窗口其实类似，但是第一重循环标记的是结束点j，这种方法下，i和j都不需要回退，时间复杂度为O(n)。

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int sum = 0;
        int i = 0;
        int min = nums.length + 1;
        for(int j = 0; j < nums.length; j++){
            sum += nums[j];
            if(sum >= target){
                while(sum >= target){
                    int newLength = j - i + 1;
                    min = newLength < min ? newLength: min;
                    sum -= nums[i++];
                }
            }
        }
        if(min < nums.length + 1) return min;
        return 0;
    }
}

[中等] 59. 螺旋矩阵 II

原题链接

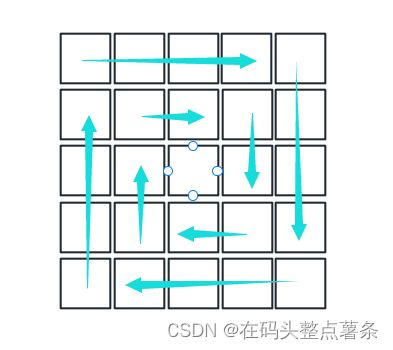
将下图这样算作画一圈，如果n是偶数，需要画n/2圈，如果n是奇数，则需要画n/2圈外额外填充中间一格

当n为6：

当n为5

class Solution {
    public int[][] generateMatrix(int n) {
        //转 n / 2 圈，奇数要额外补上一个
        int [][] answer = new int[n][n];
        int count = 1; //填充计数
        int flag = 0; //循环圈数
        while(flag < n / 2) {
            for (int i = flag; i < n - 1 - flag; i++) {
                answer[flag][i] = count++;
            }
            for (int i = flag; i < n - 1 - flag; i++) {
                answer[i][n - 1 - flag] = count++;
            }
            for (int i = n - 1 - flag; i > flag; i--) {
                answer[n - 1 - flag][i] = count++;
            }
            for (int i = n - 1 - flag; i > flag; i--) {
                answer[i][flag] = count++;
            }
            flag++;
        }
        if(n%2 != 0){
            answer[n / 2][n / 2] = count;
        }
        return answer;
    }
}