leetcode 岛屿的最大面积

695. 岛屿的最大面积

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：

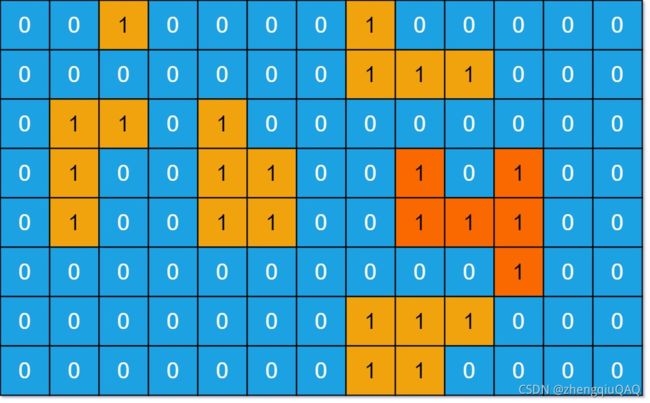
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• grid[i][j] 为 0 或 1

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/max-area-of-island。

• 遍历过的点可以赋值为0，避免重复访问。
• 广度优先搜索

class Solution {
public:
    int maxAreaOfIsland(vector>& grid) {
        int max_land = 0;
        std::queue> que_ij;
        for (int i = 0; i < grid.size(); ++i) {
            for (int j = 0; j < grid[0].size(); ++j) {
                int current_land = 0;
                que_ij.emplace(i, j);
                while (!que_ij.empty()) {
                    int x = que_ij.front().first; 
                    int y = que_ij.front().second;
                    que_ij.pop();
                    if (x < 0 || x >= grid.size() || y < 0 || y >= grid[0].size() || grid[x][y] == 0) {
                        continue;
                    }
                    ++current_land;
                    grid[x][y] = 0;
                    for (int d = 0; d < 4; ++d) {
                        int nex_x = x + dx[d];
                        int nex_y = y + dy[d];
                        que_ij.emplace(nex_x, nex_y);
                    }
                }
                max_land = std::max(max_land, current_land);
            }
        }
        return max_land;
    }
private:
    const int dx[4] = {-1, 0, 0, 1};
    const int dy[4] = {0, 1, -1, 0};
};

• 深度优先搜索

class Solution {
public:
    int maxAreaOfIsland(vector>& grid) {
        int max_land = 0;
        for (int i = 0; i < grid.size(); ++i) {
            for (int j = 0; j < grid[0].size(); ++j) {
                max_land = std::max(max_land, dfs(grid, i, j));
            }
        }
        return max_land;
    }
private:
    int dfs (vector>& grid, int x, int y) {
        if (x < 0 || x >= grid.size() || y < 0 || y >= grid[0].size() || grid[x][y] == 0) {
            return 0;
        }
        grid[x][y] = 0;
        int cur_land = 1;
        for (int d = 0; d < 4; ++d) {
            cur_land += dfs(grid, x + dx[d], y + dy[d]);
        }
        return cur_land;
    }

    const int dx[4] = {-1, 0, 0, 1};
    const int dy[4] = {0, 1, -1, 0};
};