机器学习:十大算法快速回顾
一、说明
二. 线性回归
2.1 算法描述
有没有想过数据奇才如何预测未来?输入线性回归,这是一种强大的统计工具,可以解开隐藏在连续变量中的秘密。这一切都是为了在数据迷宫中找到完美的路线,为对未来的清晰预测铺平道路。
简单线性回归模型的方程为:
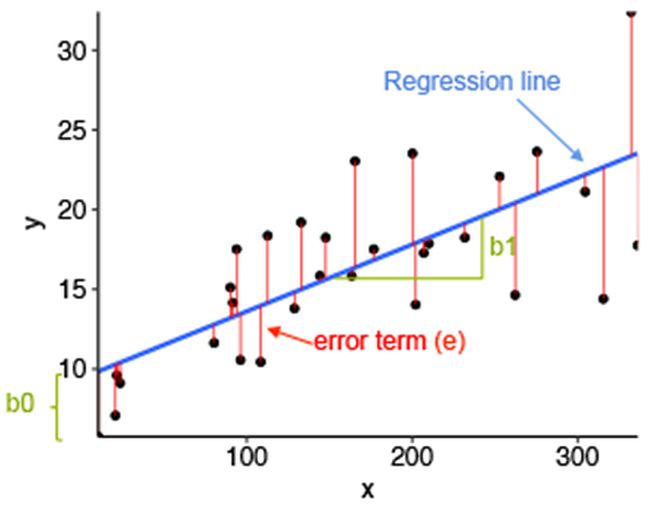
y = b0 + b1*x
其中 y 是因变量,x 是自变量,b0 是 y 截距(直线与 y 轴的交点),b1 是直线的斜率。斜率表示给定 x 变化时 y 的变化。
为了确定最佳拟合线,我们使用最小二乘法,该方法找到使预测 y 值与实际 y 值之间的平方差之和最小化的线。
但是等等,还有更多!线性回归的才华不仅仅局限于一个变量:它是一颗多才多艺的明星。来认识一下“多重线性回归”,我们可以轻松地处理多个自变量。这是秘密公式:
y = b0 + b1x1 + b2x2 + … + bn*xn
其中 x1, x2, …, xn 是自变量,b1, b2, …, bn 是相应的系数。
线性回归是解决简单和复杂预测问题的首选工具。它通过使用最小二乘法估计那些神秘系数(b0、b1、…、bn)来发挥其魔力。一旦掌握了这些数字,您就可以预测未来,无论是预测股票价格还是预测产品销售。
但是,更重要的是,线性回归是一匹值得信赖的骏马,但并不是每个谜语的答案。它在线性领域蓬勃发展,假设变量之间的关系像箭头一样笔直。然而,现实可能会更加曲折。
此外,线性回归对异常值极其敏感,这意味着如果存在任何不遵循数据总体趋势的极值,将会显着影响模型的准确性。
总而言之,线性回归作为一种强大且广泛使用的统计技术而出现,有效地揭示了两个连续变量之间的联系。它的优雅在于它的简单性,但它的预测能力却熠熠生辉。尽管如此,重要的是要记住,线性回归是在变量之间存在线性连接的假设下运行的,并且可能会受到异常值的影响,从而可能影响模型的精度。
2.2 拟合优度
有多种方法可以确定线性回归模型的拟合优度:
R 平方:R 平方是一种统计度量,表示因变量中的方差由模型中的自变量解释的比例。R 平方值为 1 表示模型解释了因变量中的所有方差,值为 0 表示模型没有解释任何方差。
调整 R 平方:调整 R 平方是 R 平方的修改版本,它考虑了模型中自变量的数量。在比较具有不同数量自变量的模型时,它可以更好地指示模型的拟合优度。
均方根误差 (RMSE):RMSE 衡量预测值与实际值之间的差异。RMSE 较低表明模型与数据的拟合效果更好。
平均绝对误差 (MAE):MAE 测量预测值与实际值之间的平均差异。MAE 越低表明模型与数据的拟合效果越好。
2.3. 线性回归中的异常值。
有没有想过为什么这些奇怪的数据点有时会影响您的线性回归预测?让我们深入了解异常值的世界及其对我们可靠的回归线的影响。但不用担心,我们有一些实用的技术可以帮助您驯服那些难以驾驭的数据点并使您的模型更加准确。包括:
删除异常值:一种选择是在训练模型之前简单地从数据集中删除异常值。然而,这可能会导致有价值信息的丢失。
转换数据:应用转换(例如记录数据日志)有助于减少异常值的影响。
使用稳健回归方法:稳健回归方法(例如 RANSAC 或 Theil-Sen)对异常值的敏感度低于传统线性回归。
使用正则化:正则化可以通过在成本函数中添加惩罚项来帮助防止由异常值引起的过度拟合。
最佳方法取决于具体的数据集和分析目标。
2.3 逻辑回归
你有没有思考过?机器如何做出决定,例如电子邮件是否是垃圾邮件或客户是否可能离开?逻辑回归是机器学习领域的重要工具。它就像一个侦探,使用来自多个来源的统计线索来预测结果。
这种方法依赖于一个巧妙的数学技巧,即逻辑函数。将其视为将数字转化为概率的翻译器,巧妙地压缩在 0 和 1 之间。然后,这些概率指导我们的人工智能朋友对未来做出明智的预测。
逻辑回归模型由以下方程表示:
P(y=1|x) = 1/(1+e^-(b0 + b1x1 + b2x2 + … + bn*xn))
其中 P(y=1|x) 是给定输入变量 x 时结果 y 为 1 的概率,b0 是截距,b1, b2, …, bn 是输入变量 x1, x2, … 的系数, xn。
通过在数据集上训练我们的模型并使用梯度下降等优化技巧对其进行调整,我们发现了秘密武器 - 系数!这些小宝石可以最小化我们的成本函数(通常是对数损失)并掌握做出预测的关键。
但是等等,还有更多!一旦我们的模型全部训练完毕,它就会成为一个预测引擎。我们只需向它提供新数据,它就会计算出结果为 1 的概率。问题是什么?决定何时将其称为“1”或“0”。我们通常将门槛设置为 0.5,但这就是阈值。是可以调节的!这完全取决于任务以及您愿意在“哎呀”和“错过了”之间的微妙界限上跳舞的程度
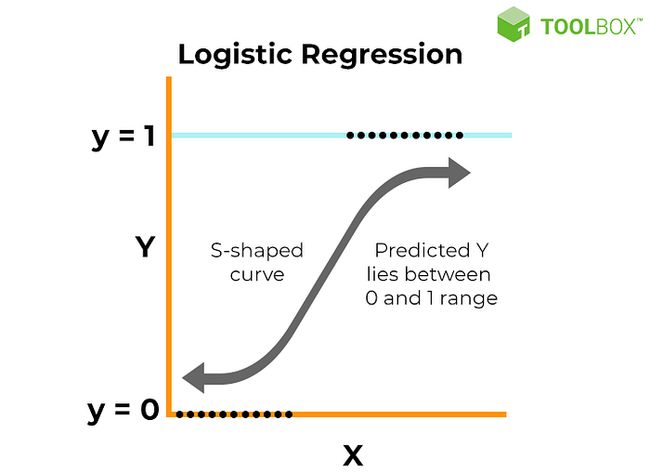
下图是逻辑回归模型的示意图:
在此图中,输入变量 x1 和 x2 用于预测二进制结果 y。逻辑函数将输入变量映射为概率,然后使用该概率对结果进行预测。系数 b1 和 b2 通过在数据集上训练模型来确定,阈值设置为 0.5。
总之,逻辑回归是预测二元结果的强大技术,广泛应用于机器学习和数据分析。它易于实现、解释,并且可以轻松地进行正则化以防止过度拟合。
三、支持向量机(SVM)
想象一下:一个数学奇迹,一类算法不仅从数据中学习,而且以一种令人着迷的优雅来学习。欢迎来到支持向量机(简称 SVM)的世界。在机器学习领域,SVM 既是基础又是启示。他们拥有独特的能力来剖析复杂的数据环境,以外科手术般的精确度划定决策边界。和我一起踏上揭开 SVM 神秘面纱的旅程,探索它们如何利用从噪声中分离信号的艺术,引导我们完成分类和回归任务的复杂领域。在本次探索结束时,您不仅会了解 SVM 的内部工作原理,还会欣赏其数学工艺之美。
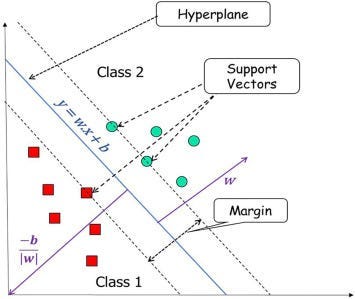
支持向量机 (SVM) 是一种监督学习算法,可用于分类或回归问题。SVM 背后的主要思想是通过最大化边距(边界与每个类最近的数据点之间的距离)来找到分隔数据中不同类的边界。这些最接近的数据点称为支持向量。
当数据不可线性分离(这意味着数据不能用直线分离)时,SVM 特别有用。在这些情况下,SVM 可以使用一种称为核技巧的技术将数据转换到更高维的空间,其中可以找到非线性边界。SVM 中使用的一些常见核函数包括多项式、径向基函数 (RBF) 和 sigmoid。
想象一下,有一个多功能工具可以在复杂数据领域蓬勃发展,即使面对比样本更多的特征,也能轻松处理高维空间并提供一流的性能。了解支持向量机 (SVM)。它们在内存效率方面表现出色,仅在存储中保留必要的支持向量,而不是整个数据集。然而,与任何强大的工具一样,SVM 也有其细微差别。选择正确的核函数和参数调整可能至关重要。另外,由于训练时间可能很长,它们可能不是庞大数据集的首选。
优点:
1. 在高维空间中有效:即使当特征数量大于样本数量时,SVM 也具有令人满意的性能。
2. 内存效率高:SVM 只需要存储支持向量,而不需要存储整个数据集,因此内存效率高。
3. 多功能:SVM 可用于分类和回归问题,并且可以使用核技巧处理非线性可分离数据。
4. 对噪声和异常值具有鲁棒性:SVM 对数据中的噪声和异常值具有鲁棒性,因为它们仅依赖于支持向量。
缺点:
1. 对核函数和参数的选择敏感:SVM 的性能高度依赖于核函数的选择和算法参数。
2. 不适合大型数据集:对于大型数据集,SVM 的训练时间可能会相当长。
3. 解释结果困难:解释 SVM 的结果可能很困难,特别是在使用非线性核时。
4. 不适用于重叠类:当类有明显重叠时,SVM 可能会遇到困难。
总之,SVM 是一种强大且通用的机器学习算法,可用于分类和回归问题,特别是当数据不可线性分离时。然而,它们可能对核函数和参数的选择敏感,不适合大型数据集,并且难以解释结果。
四、决策树
欢迎来到决策树的迷人世界! 在机器学习领域,这些直观的算法是您以结构化和逻辑方式做出复杂决策的可靠指南。想象一棵树,它的树枝代表不同的选择,引导你得到最好的结果。在这个旅程中,我们将揭开决策树背后的秘密,揭开它们的内部运作原理,并向您展示它们如何成为您解决现实问题的盟友
决策树是一种用于分类和回归任务的机器学习算法。它们是决策的强大工具,可用于对变量之间的复杂关系进行建模。
决策树是一种树状结构,每个内部节点代表一个决策点,每个叶节点代表最终结果或预测。该树是通过根据输入特征的值递归地将数据分割成子集来构建的。目标是找到最大化不同类别或目标值之间分离的分割。
构建决策树的过程从选择根节点开始,根节点是最好地将数据分为不同类别或目标值的特征。然后根据该特征的值将数据分成子集,并对每个子集重复该过程,直到满足停止标准。停止标准可以基于子集中的样本数量、子集的纯度或树的深度。
决策树存在一些常见的挑战。一个关键问题是它们倾向于过度拟合数据,尤其是当树变得很深并且分支广泛时。当树变得过于复杂时,就会发生过度拟合,捕获噪声而不是实际模式。这可能会损害其在新的、未见过的数据上的性能。但不用担心!我们有修剪、正则化和交叉验证等技巧来控制过度拟合。
另一个挑战是它们对输入特征顺序的敏感性。对功能进行洗牌,最终可能会得到一种完全不同的树结构,但并不总是最好的。但不要害怕!随机森林和梯度提升等技术可以解决这一问题,确保做出更稳健的决策。
总之,决策树在决策和预测建模领域成为一种有效且适应性强的工具。它们天生的简单性和可解释性使它们平易近人,但必须意识到它们过度拟合数据的倾向。为了应对这一挑战,该领域引入了一系列技术。其中包括修剪(一种修剪形式)和规则化(类似于保持平衡)。交叉验证是我们的指南针,而随机森林和梯度提升等集合则在我们充分发挥决策树潜力的过程中充当经验丰富的指南。
五、随机森林
想象一下一个强大的机器学习工具,它结合了大众的智慧和专家的精确度。这正是随机森林模型带来的效果。在数据科学领域,它经常被誉为游戏规则的改变者,今天,我们将踏上揭开其内部运作神秘面纱的旅程。因此,系好安全带,准备好探索这种巧妙的算法如何使复杂的预测看起来像在公园散步一样简单。
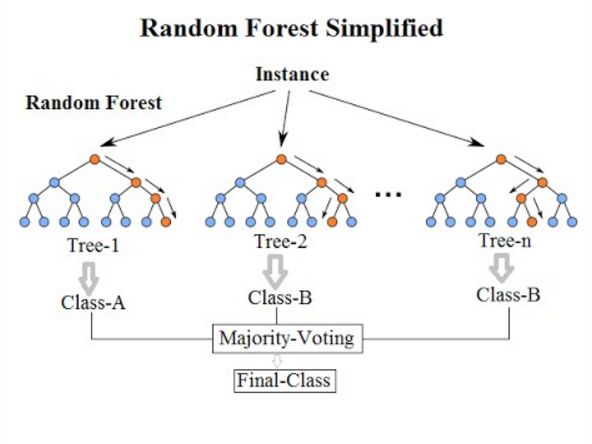
随机森林是一种集成机器学习算法,可用于分类和回归任务。它是多个决策树的组合,其中每棵树都是使用数据的随机子集和特征的随机子集来生长的。最终的预测是通过对森林中所有树木的预测进行平均来做出的。
使用多个决策树背后的想法是,虽然单个决策树可能容易过度拟合,但决策树的集合或森林可以降低过度拟合的风险并提高模型的整体准确性。
构建随机森林的过程首先使用一种称为引导的技术创建多个决策树。Bootstrapping 是一种统计方法,涉及从原始数据集中随机选择数据点并进行替换。这会创建多个数据集,每个数据集都有一组不同的数据点,然后用于训练单个决策树。
随机森林的主要优点之一是它比单个决策树更不容易过度拟合。多棵树的平均可以消除误差并减少方差。随机森林在高维数据集和具有大量 calcategories 变量的数据集中也表现良好。
随机森林的缺点是训练和预测的计算成本可能很高。随着森林中树木数量的增加,计算时间也会增加。此外,随机森林比单个决策树的可解释性更差,因为更难理解每个特征对最终预测的贡献。
总之,随机森林是一种强大的集成机器学习算法,可以提高决策树的准确性。它不太容易过度拟合,并且在高维和分类数据集中表现良好。然而,与单个决策树相比,它的计算成本较高且可解释性较差。
六、朴素贝叶斯
朴素贝叶斯算法。如果您想知道这种聪明且出奇简单的技术如何在解决现实世界问题中发挥如此强大的力量,那么您来对地方了。在这次探索中,我们将揭开朴素贝叶斯的内部工作原理,揭开其基本概念的神秘面纱,并揭示其实际应用。
朴素贝叶斯是一种简单高效的机器学习算法,基于贝叶斯定理,用于分类任务。它被称为“朴素”,因为它假设数据集中的所有特征都是相互独立的,而现实世界数据中的情况并不总是如此。尽管有这样的假设,朴素贝叶斯被发现在许多实际应用中表现良好。
该算法通过使用贝叶斯定理来计算给定输入特征值的给定类别的概率。贝叶斯定理指出,给定一些证据(在本例中为特征值)的假设(在本例中为类别)的概率与给定假设的证据的概率乘以假设的先验概率成正比。
朴素贝叶斯算法可以使用不同类型的概率分布(例如高斯分布、多项式分布和伯努利分布)来实现。高斯朴素贝叶斯用于连续数据,多项式朴素贝叶斯用于离散数据,伯努利朴素贝叶斯用于二进制数据。
它的突出优势之一在于它的简单性——易于掌握,这使其成为机器学习新手的绝佳起点。此外,它在应用于垃圾邮件分类和情绪分析等任务时表现非常出色。然而,它有其怪癖。朴素贝叶斯假设特征是独立的,但现实世界数据中的情况并不总是如此。在功能依赖性发挥重要作用的情况下,这种“天真的”假设可能会导致次优结果。尽管如此,通过正确的数据预处理并了解其局限性,朴素贝叶斯可以成为机器学习工具包中的强大工具。
最后,让我们来了解一下朴素贝叶斯——一种非常简单且高效的机器学习算法。它依赖于贝叶斯定理,并且在分类任务方面表现得最为出色。处理高维数据集和优雅地处理缺失数据是它的优势。然而,有一个问题:朴素贝叶斯在特征完全独立的假设下运行,如果不满足这一概念,偶尔会出错,可能会产生不太精确的预测。了解这种权衡将帮助您有效地利用其力量。
七.KNN _
想象一下:你有一个图书馆,里面装满了书籍,每本都充满了知识,你的任务是将它们分类。挑战在于,书上没有标签,你也无法通过封面来判断它们。这正是 K 最近邻 (KNN) 发挥作用的地方,就像熟练的图书管理员一样,能够根据书籍的内容将书籍与其类型进行匹配。在对 KNN 的探索中,我们踏上了揭开这种多功能算法的内部工作原理的旅程,并发现它如何对数据点进行分类,就像我们的图书管理员在没有事先标签的情况下熟练地对书籍进行分类一样
K 最近邻 (KNN) 是一种简单而强大的算法,用于机器学习中的分类和回归任务。它基于这样的想法:相似的数据点往往具有相似的目标值。该算法的工作原理是查找给定输入的 k 个最近数据点,并使用最近数据点的多数类或平均值来进行预测。
构建 KNN 模型的过程从选择 k 值开始,k 是预测时考虑的最近邻居的数量。然后将数据分为训练集和测试集,训练集用于查找最近的邻居。为了对新输入进行预测,该算法计算输入与训练集中每个数据点之间的距离,并选择 k 个最近的数据点。然后使用最近数据点的多数类或平均值作为预测。
KNN 的主要优点之一是其简单性和灵活性。它可用于分类和回归任务,并且不对底层数据分布做出任何假设。此外,它可以处理高维数据,并可用于监督和无监督学习。
KNN 的主要缺点是其计算复杂性。随着数据集大小的增加,查找最近邻居所需的时间和内存可能会变得非常大。此外,KNN 对 k 的选择很敏感,并且找到 k 的最佳值可能很困难。
总而言之,机器学习领域的多功能宝石。该算法虽然非常简单,但在分类和回归任务方面却很有用。它的辉煌之处在于相信具有相似性的数据点往往有着相似的命运。
KNN 以其适应性而引人注目——甚至可以处理最棘手的高维数据。此外,它还优雅地服务于监督学习和非监督学习,使其成为一个全面的工具。
八、K-均值
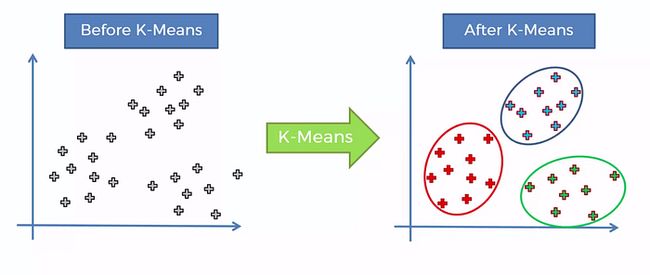
欢迎来到数据集群的有趣世界,这里的模式来自海量的信息。今天,我们踏上 K-Means 领域的旅程,这是一种令人着迷的算法,几十年来一直是无监督学习的基石。想象一下,能够将相似的数据点分组到集群中,从而揭示数据集中的隐藏结构
K-means 是一种用于聚类的无监督机器学习算法。聚类是将相似的数据点分组在一起的过程。K-means 是一种基于质心的算法或基于距离的算法,我们计算将点分配给簇的距离。
该算法的工作原理是随机选择 k 个质心,其中 k 是我们想要形成的簇的数量。然后将每个数据点分配给具有最近质心的簇。一旦分配了所有点,质心将被重新计算为簇中所有数据点的平均值。重复此过程,直到质心不再移动或点对簇的分配不再改变。
K-means 的主要优点之一是其简单性和可扩展性。它易于实现并且可以有效地处理大型数据集。此外,它是一种快速且鲁棒的算法,已广泛应用于图像压缩、市场细分和异常检测等许多应用中。
K 均值的主要缺点是它假设簇是球形且大小相等,但现实世界数据中的情况并非总是如此。此外,它对质心的初始放置和 k 的选择很敏感。它还假设数据是数字的,如果数据不是数字的,则必须在使用算法之前对其进行转换。
简而言之,K-means 是您值得信赖的无监督机器学习工具,用于将数据点分组为集群。它的秘密武器?该算法的预感是相似的数据伙伴更喜欢一起出去玩。K-means 的酷之处在于它的简单性和多功能性 - 难怪它成为许多应用程序的首选。但问题是:K 均值有一些怪癖。它假设簇是圆形的且大小均匀,对初始簇中心的放置位置非常挑剔,并且对簇的数量(对您来说就是“k”)很挑剔。
九. 降维算法
降维是一种用于减少数据集中特征数量同时保留重要信息的技术。它用于提高机器学习算法的性能并使数据可视化更容易。有多种可用的降维算法,包括主成分分析 (PCA)、线性判别分析 (LDA) 和 t 分布随机邻域嵌入 (t-SNE)。
主成分分析 (PCA) 是一种线性降维技术,它使用正交变换将一组相关变量转换为一组称为主成分的线性不相关变量。PCA 对于识别数据模式和降低数据维度而不丢失重要信息非常有用。
线性判别分析(LDA)是一种监督降维技术,用于为分类任务找到最具判别性的特征。LDA 最大化了低维空间中类之间的分离。
t 分布随机邻域嵌入 (t-SNE) 是一种非线性降维技术,对于可视化高维数据特别有用。它使用高维数据点对上的概率分布来查找保留数据结构的低维表示。
降维技术的主要优点之一是它们可以通过降低计算成本和降低过度拟合的风险来提高机器学习算法的性能。此外,它们还可以通过将维度数量减少到更易于管理的数量来使数据可视化变得更容易。
降维技术的主要缺点是在降维过程中可能会丢失重要信息。此外,降维技术的选择取决于数据的类型和手头的任务,并且可能很难确定要保留的最佳维数。
总之,降维是一种用于减少数据集中特征数量同时保留重要信息的技术。有多种降维算法可用,例如 PCA、LDA 和 t-SNE,它们可用于识别数据模式、提高机器学习算法的性能并使数据可视化更容易。然而,在降维过程中可能会丢失重要信息,并且降维技术的选择取决于数据的类型和手头的任务。
十.梯度Boosting算法和AdaBoosting算法
梯度提升和 AdaBoost 是两种流行的集成机器学习算法,可用于分类和回归任务。这两种算法都通过组合多个弱模型来创建一个强大的最终模型。
梯度提升是一种迭代算法,它以向前阶段的方式构建模型。它首先将一个简单的模型(例如决策树)拟合到数据中,然后添加其他模型来纠正先前模型所犯的错误。每个新模型都适合损失函数相对于先前模型的预测的负梯度。最终模型是所有单独模型的加权和。
AdaBoost 是自适应增强 (Adaptive Boosting) 的缩写,是一种类似的算法,也以前向阶段方式构建模型。然而,它的重点是通过调整训练数据的权重来提高弱模型的性能。在每次迭代中,算法都会关注被先前模型错误分类的训练样本,并调整这些样本的权重,以便它们在下一次迭代中被选择的概率更高。最终模型是所有单独模型的加权和。
人们发现梯度增强和 AdaBoost 在许多实际应用中都可以生成高精度模型。这两种算法的主要优点之一是它们可以处理多种数据类型,包括分类数据和数值数据。此外,这两种算法都可以处理缺失值的数据,并且对异常值具有鲁棒性。
这两种算法的主要缺点之一是它们的计算成本可能很高,特别是当集成中的模型数量很大时。此外,他们可能对基础模型和学习率的选择很敏感。
总之,梯度提升和 AdaBoost 是两种流行的集成机器学习算法,可用于分类和回归任务。这两种算法都通过组合多个弱模型来创建一个强大的最终模型。人们发现,两者都可以在许多实际应用中产生高度准确的模型,但它们的计算成本可能很高,并且对基础模型和学习率的选择很敏感。