模糊控制基础

模糊控制的过程：输入->输入模糊化->模糊运算->运算结果解模糊化->输出

理论基础

模糊化

隶属函数

隶属度函数：若对论域（研究的范围）U中的任一元素x，都有一个数A(x)∈[0，1]与之对应，则称A为U上的模糊集，A(x )称为x对A的隶属度。当x在U中变动时，A( x)就是一个函数，称为A的隶属函数。
用人话来说，隶属度函数就是相关程度，不相关为0，相关为1，部分相关为0.x

例如：下图所示的隶属函数(NB NS ZO PS PB)图形中，对于-0.4是属于NB还是NS是无法给出确定的答案的，只能说-0.4属于NB和属于NS的可能性都为0.37

隶属函数的分类

内容来源于 Matlab-帮助

1、广义钟形隶属函数


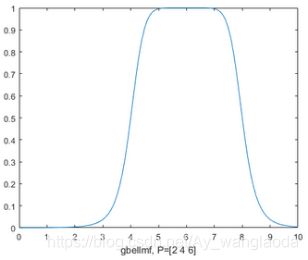
2、高斯隶属函数


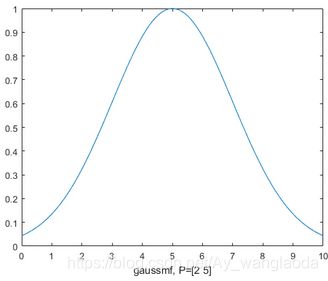
3、高斯组合隶属函数


4、三角隶属函数


5、梯形隶属函数


6、S形隶属函数


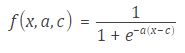
7、双S形隶属函数


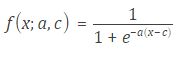
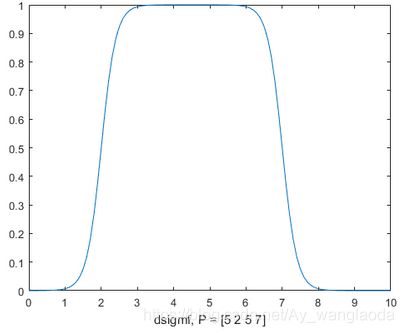
8、双S乘积形隶属函数


9、Z形隶属函数


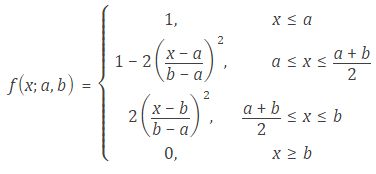
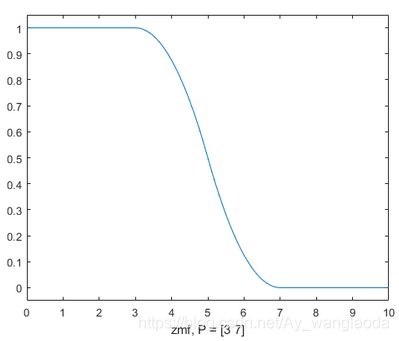
10、Ⅱ形隶属函数


11、S状隶属函数

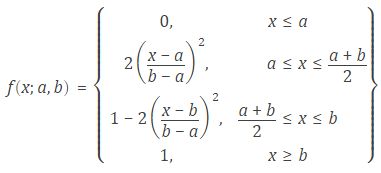
解模糊

重心法

fnum = 0;
fden = 0;
for i = 1:1:3
    for j = 1:1:3
        fnum = fnum + u1(i)*u2(j)*U(i,j);      %    U 为模糊规则表（3*3）
        fden = fden + u1(i)*u2(j);
    end
end   
u(k) = fnum/(fden + 0.01);

最大隶属度法

选择隶属度最大的元素作为输出

系数加权平均法

在最大隶属度法的基础之上的改进，权重 ki 为可调参数。

离散化系统仿真

以被控对象 G(s) = 133/s² + 25s ，目标信号为阶跃信号为例

建立模糊系统

%   fuzzy inference system
% 	输入误差 e 以及 de ，经过模糊系统计算出 △kp，△ki，结合 pid 进行控制
clear all;
close all;

a = newfis('fuzzy_pid');                          % 输入 e
a = addvar(a,'input','e',[-1,1]);
a = addmf(a,'input',1,'N','zmf',[-1,-1/3]);
a = addmf(a,'input',1,'Z','trimf',[-2/3,0,2/3]);
a = addmf(a,'input',1,'P','smf',[1/3,1]);

a = addvar(a,'input','de',[-1,1]);                          % 输入 de
a = addmf(a,'input',2,'P','smf',[1/3,1]);

a = addvar(a,'output','kp',[-10,10]);                          % 输出 kp
a = addmf(a,'output',1,'N','zmf',[-10,-3]);
a = addmf(a,'output',1,'Z','trimf',[-5,0,5]);
a = addmf(a,'output',1,'P','smf',[3,10]);

a = addvar(a,'output','ki',[-3,3]);                          % 输出 ki
a = addmf(a,'output',2,'N','zmf',[-3,-1]);
a = addmf(a,'output',2,'Z','trimf',[-2,0,2]);
a = addmf(a,'output',2,'P','smf',[1,3]);

rulelist = [1 1 1 2 1 1
            1 2 1 2 1 1
            1 3 1 2 1 1
            
            2 1 1 3 1 1
            2 2 3 3 1 1
            2 3 3 3 1 1
            
            3 1 3 2 1 1
            3 2 3 2 1 1
            3 3 3 2 1 1];

a = addrule(a,rulelist);
a = setfis(a,'DefuzzMethod','centroid');
writefis(a,'fuzzy_pid');

---

fis = addvar(fis,varType,varName,varBounds)
fis = addvar(fis,输入/输出,变量名,变量范围)

---

a = addmf(fis,varType,varIndex,mfName,mfType,mfParams)
a = addmf(fis,输入/输出,成员函数变量索引,成员变量名,成员类型,成员变量的范围)

---

rulelist = [a,b,c,d]; % 以单输入单输出为例，rulelist矩阵列数为:输入个数+输出个数+2
rulelist = [输入成员变量索引，输出成员变量索引，权重，各条件的关系];

---

主程序

clear all;
close all;

a = readfis('fuzzy_pid');

ts = 0.001;
sys = tf(133,[1 25 0]);
dsys = c2d(sys,ts,'z');
[num,den] = tfdata(dsys,'v');

kp0 = 0;    ki0 = 0;           %	kp 和 ki 的初始值为0
u_2 = 0;  u_1 = 0;
y_2 = 0;  y_1 = 0;
e_1 = 0;    ec_1 = 0;   ei = 0;

for k = 1:1:2000
    time(k) = k*ts;
    
    yd(k) = 1;
    %   using fuzzy inference system to tunning PI
    k_pid = evalfis([e_1,ec_1],a);       %	执行模糊推理计算
    kp(k) = kp0 + k_pid(1);
    ki(k) = ki0 + k_pid(2);
    u(k) = kp(k)*e_1 + ki(k)*ei;
    
    y(k) = -den(3)*y_2 - den(2)*y_1 + num(3)*u_2 + num(2)*u_1;
    e(k) = yd(k) - y(k);
    
    u_2 = u_1;  u_1 = u(k);
    y_2 = y_1;  y_1 = y(k);
    
    ei = ei + e(k)*ts;
    ec(k) = e(k) - e_1;
    e_1 = e(k);
    ec_1 = ec(k);
    
end

figure(1)
plot(time,yd,'r',time,y,'b');grid
figure(2)
plot(time,e,'r',time,ec,'b');grid

仿真结果

信号跟踪：

红色为目标信号，蓝色为实际输出信号

误差：

红色为误差信号，蓝色为误差信号的变化率