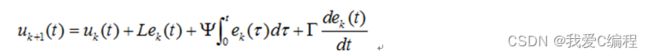m基于matlab的模糊控制器仿真实现,采用matlab编程方式定义模糊规则,隶属函数等

目录

1.算法仿真效果

2.MATLAB核心程序

3.算法涉及理论知识概要

4.完整MATLAB

---

1.算法仿真效果

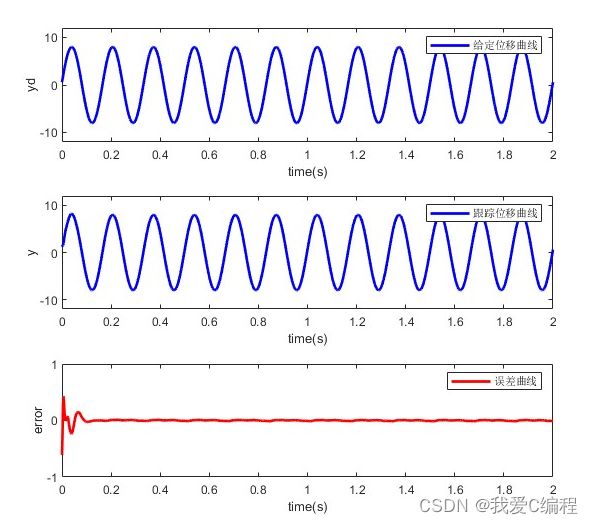
matlab2022a仿真结果如下：

 

 

2.MATLAB核心程序

.....................................................................
a=addrule(a,rulelist); 
a=setfis(a,'DefuzzMethod','mom'); 
writefis(a,'fuzzpid'); 
a=readfis('fuzzpid'); 
%显示规则
showrule(a) 

%%
%控制对象的设置
%采样时间
ts        = 0.002;
%产生连续形式的传递函数
Gp        = tf([16],[10,1.2,6]);
%产生离散形式的传递函数
Gpz       = c2d(Gp,ts,'z');
%将传递函数转换为差分式子
[num,den] = tfdata(Gpz,'v');

%%
%控制算法初始参数
L         = 100;
fai       = 0.1;
F         = 50;
%此变量分别保存误差，误差积分以及误差导数
Err       = [0,0,0]';
%延迟变量
y_1       = 0;
y_2       = 0;
u_1       = 0;
u_2       = 0;
e_1       = 0; 
ei        = 0;
ed        = 0;
%%
%迭代过程
Time      = 1001; 
u         = zeros(1,Time);      
Pk        = L*ones(1,Time);   
Ik        = fai*ones(1,Time);   
Dk        = F*ones(1,Time);   
M         = 8;
Ed        = 0.0; 
Ecd       = 0.0; 

for i=0:1:M
    for k=1:1:Time
        %产生时间变量
        time(k) = (k-1)*ts;
        %给定轨迹输入
        yd(k)   = 8*sin(6*2*pi*k*ts);
        
        %根据模糊规则，进行PID参数的更新
        k_pid   = evalfis([Ed,Ecd],a); 
        Pk(k)   = L  + k_pid(1); 
        Ik(k)   = fai+ k_pid(2); 
        Dk(k)   = F  + k_pid(3); 

        %控制对象模型的输出
.......................................................................
        %使用延迟程序起到存储器的功能
        u2(k)   = u(k);
        e_1     = e(k);
        y_2     = y_1;
        y_1     = y(k);
        u_2     = u_1;
        u_1     = u2(k);
        Ed      = e(k);
        Ecd     = e(k)-e_1;
    end    
    i=i+1;
end 

figure;
subplot(311);
plot(time,yd,'b','linewidth',2);
xlabel('time(s)');
ylabel('yd');
legend('给定位移曲线');
axis([0,2,-12,12]);

subplot(312);
plot(time,y,'b','linewidth',2);
xlabel('time(s)');
ylabel('y');
legend('跟踪位移曲线');
axis([0,2,-12,12]);

subplot(313);
plot(time,yd-y,'r','linewidth',2);
xlabel('time(s)');
ylabel('error'); 
legend('误差曲线');
axis([0,2,-1,1]);

figure;
subplot(311);
plot(time,Pk,'b','linewidth',1);
xlabel('time(s)');
ylabel('L');
legend('参数L的模糊PID方式下的自适应变化');


subplot(312);
plot(time,Ik,'b','linewidth',1);
xlabel('time(s)');
ylabel('fai');
legend('参数fai的模糊PID方式下的自适应变化');


subplot(313);
plot(time,Dk,'b','linewidth',1);
xlabel('time(s)');
ylabel('F'); 
legend('参数F的模糊PID方式下的自适应变化');

figure;
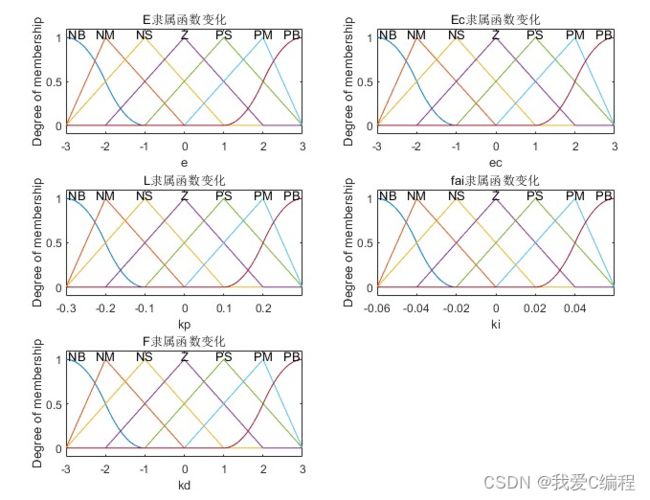
subplot(321);plotmf(a,'input',1);  title('E隶属函数变化');
subplot(322);plotmf(a,'input',2);  title('Ec隶属函数变化');
subplot(323);plotmf(a,'output',1); title('L隶属函数变化');
subplot(324);plotmf(a,'output',2); title('fai隶属函数变化');
subplot(325);plotmf(a,'output',3); title('F隶属函数变化');
figure;
plotfis(a); 
08_027_m

3.算法涉及理论知识概要

       利用模糊数学的基本思想和理论的控制方法。在传统的控制领域里，控制系统动态模式的精确与否是影响控制优劣的最主要关键。系统动态的信息越详细，则越能达到精确控制的目的。
       然而，对于复杂的系统，由于变量太多，往往难以正确的描述系统的动态，于是工程师便利用各种方法来简化系统动态，以达成控制的目的，但却不尽理想。换言之，传统的控制理论对于明确系统有强而有力的控制能力，但对于过于复杂或难以精确描述的系统，则显得无能为力了。因此便尝试着以模糊数学来处理这些控制问题。

模糊控制器包括四部分：
(1)模糊化。主要作用是选定模糊控制器的输入量，并将其转换为系统可识别的模糊量，具体包含以下三步：
第一，对输入量进行满足模糊控制需求的处理;
第二，对输入量进行尺度变换;
第三，确定各输入量的模糊语言取值和相应的隶属度函数。
(2)规则库。根据人类专家的经验建立模糊规则库。模糊规则库包含众多控制规则，是从实际控制经验过渡到模糊控制器的关键步骤。
(3)模糊推理。主要实现基于知识的推理决策。
(4)解模糊。主要作用是将推理得到的控制量转化为控制输出。

第一部分：控制存储器

    这个部分比较简单，就是将当前时刻的数据进行保存，作为下一时刻的学习控制算法模块的输出的相加项，然后得到新输出。其对应的程序如下所示：

  

第二部分：被控对象

    控制对象，在matlab编程的时候，我们一般使用的是传递函数来标示，在参考文献中，关于控制对象的介绍似乎没有讲，一般这种情况，我们设置一个传递函数作为控制对象来研究我们的控制算法。

    很多研究控制算法的课题，如果不知道控制对象具体的传递函数表达式，我们一般都设置一个传递函数作为控制对象进行控制算法的研究，如果你在自己的论文中已经设计了一个控制对象的传递函数，那么直接替换即可。

    在本课题中，控制对象的传递函数我们设置为如下的表达式：

   

第三部分：学习控制算法

    这个部分是程序算法的重点，这里我们重点介绍 一下这个部分的实现过程。首先我们要做的是模糊PID控制器，论文中关于PID学习控制算法的主要表达式为：

        然后这里控制器采用模糊PID控制器，然后迭代过程采用公式6.3来进行。注意，由于加入遗忘因子的话，在模糊PID中，收敛值收敛到0会变得非常的困难，故这里我们使用不带遗忘因子的公式。 

4.完整MATLAB

V