OpenGL坐标变换

1. 坐标系统间的变换

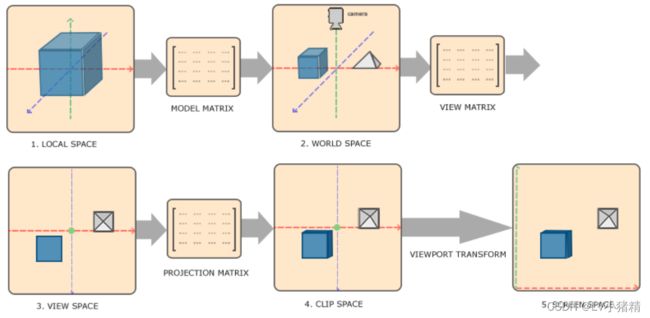
在渲染管线中，物体的顶点在最终转化为屏幕坐标之前还会被变换到多个坐标系统(Coordinate System)。将物体的坐标变换到几个过渡坐标系(Intermediate Coordinate System)的优点在于，在这些特定的坐标系统中，一些操作或运算更加方便和容易。比较重要的有5个不同的坐标系统：

• 局部空间(Local Space，或者称为物体空间(Object Space))
• 世界空间(World Space)
• 观察空间(View Space，或者称为视觉空间(Eye Space))
• 裁剪空间(Clip Space)
• 屏幕空间(Screen Space)

以上的坐标转换就是一个顶点在最终被转化为片段之前需要经历的所有不同状态

而坐标变换需要用到变换矩阵，其中最重要的是MVP矩阵。模型矩阵（Model）、观察矩阵（View）、投影矩阵（Projection）。顶点坐标起始于局部空间(Local Space)，在这里它称为局部坐标(Local Coordinate)，它在之后会变为世界坐标(World Coordinate)，观察坐标(View Coordinate)，裁剪坐标(Clip Coordinate)，并最后以屏幕坐标(Screen Coordinate)的形式呈现。整个流程如下所示：

流程中各个坐标的解释如下：

1. 局部坐标是对象相对于局部原点的坐标，也是物体起始的坐标。
2. 世界空间坐标是处于一个更大的空间范围的。这些坐标相对于世界的全局原点，它们会和其它物体一起相对于世界的原点进行摆放。
3. 观察空间坐标使得每个坐标都是从摄像机或者说观察者的角度进行观察的。
4. 裁剪坐标会被处理至-1.0到1.0的范围内，并判断哪些顶点将会出现在屏幕上。
5. 屏幕坐标，使用一个叫做视口变换(Viewport Transform)的过程。视口变换将位于-1.0到1.0范围的坐标变换到由glViewport函数所定义的坐标范围内。最后变换出来的坐标将会送到光栅器，将其转化为片段。

1.1 局部空间

局部空间是指物体所在的坐标空间，即对象最开始所在的地方。想象创建了一个立方体。立方体的原点位于(0, 0, 0)，即便它有可能最后在程序中处于完全不同的位置。甚至有可能创建的所有模型都以(0, 0, 0)为初始位置（然而它们会最终出现在世界的不同位置）。所以，刚开始模型的所有顶点都是在局部空间中。

1.2 世界空间

如果将所有的物体导入到程序当中，有可能会全挤在世界坐标的原点(0, 0, 0)，显然这并不是想要得到的结果。希望为每一个物体定义一个位置，从而能在更大的世界中放置并渲染它们。物体的坐标将会从局部变换到世界空间；该变换由模型矩阵(Model Matrix)实现的。

模型矩阵是一种变换矩阵，它能通过对物体进行位移、缩放、旋转来改变其位置。

1.3 观察空间

观察空间经常被称为OpenGL的摄像机(Camera)（所以有时也称为摄像机空间(Camera Space)或视觉空间(Eye Space)）。观察空间是将世界空间坐标转化为用户视野前方的坐标而产生的结果。因此观察空间就是从摄像机的视角所观察到的空间。而这通常是由一系列的位移和旋转的组合来完成，平移/旋转场景从而使得特定的对象被变换到摄像机的前方。这些组合在一起的变换通常存储在一个观察矩阵(View Matrix)里，它被用来将世界坐标变换到观察空间。

裁剪空间

在一个顶点着色器运行的最后，OpenGL期望所有的坐标都能落在一个特定的范围内，且任何在这个范围之外的点都应该被裁剪掉(Clipped)。被裁剪掉的坐标就会被忽略，所以剩下的坐标就将变为屏幕上可见的片段。这也就是裁剪空间(Clip Space)的由来。

为了将顶点坐标从观察变换到裁剪空间，需要定义一个投影矩阵(Projection Matrix)，它指定了一个范围的坐标，比如在每个维度上的-1000到1000。投影矩阵会将在这个指定的范围内的坐标变换为标准化设备坐标的范围(-1.0, 1.0)。所有在范围外的坐标不会被映射到在-1.0到1.0的范围之间，所以会被裁剪掉。
将观察坐标变换为裁剪坐标的投影矩阵分为两种不同的形式，正射投影矩阵(Orthographic Projection Matrix)和透视投影矩阵(Perspective Projection Matrix)

1.4 屏幕空间

这一阶段之后，最终的坐标将会被映射到屏幕空间中（使用glViewport中的设定），并被变换成片段。

1.5 变换矩阵的组合

为上述的每一个步骤都创建了一个变换矩阵：模型矩阵、观察矩阵和投影矩阵。一个顶点坐标将会根据以下过程被变换到裁剪坐标：
$V_{clip}=M_{\text{projection }}\cdot M_{\text{view }}\cdot M_{\text{model }}\cdot V_{\text{local }}$
注意矩阵运算的顺序是相反的（记住我们需要从右往左阅读矩阵的乘法）。最后的顶点应该被赋值到顶点着色器中的gl_Position，OpenGL将会自动进行透视除法和裁剪，OpenGL会使用glViewPort内部的参数来将标准化设备坐标映射到屏幕坐标，这个过程称为视口变换。

---

2. 实现

• 首先创建模型矩阵（Model Matrix）【局部空间】➡【世界空间】
  模型矩阵包含了位移、缩放与旋转等操作它们会被应用到所有物体的顶点上，以变换它们到全局的世界空间

glm::mat4 model;
model = glm::rotate(model, glm::radians(-55.0f), glm::vec3(1.0f, 0.0f, 0.0f));//这边仅让其旋转

• 接下来是观察矩阵（View Matrix）【世界空间】➡【观察空间】
  想要在场景里面稍微往后移动，将摄像机向后移动，和将整个场景向前移动是一样的。我们以相反于摄像机移动的方向移动整个场景。因为我们想要往后移动，并且OpenGL是一个右手坐标系(Right-handed System)，所以我们需要沿着z轴的正方向移动。我们会通过将场景沿着z轴负方向平移来实现。它会给我们一种我们在往后移动的感觉。

glm::mat4 view;
// 注意，我们将矩阵向我们要进行移动场景的反方向移动。
view = glm::translate(view, glm::vec3(0.0f, 0.0f, -3.0f));

• 最后需要是投影矩阵（Projection Matrix）【观察空间】➡【裁剪空间】
  场景中使用透视投影，代码如下：

glm::mat4 projection;
projection = glm::perspective(glm::radians(45.0f), screenWidth / screenHeight, 0.1f, 100.0f);//glm::radians(45.0f) FOV 视场， 0.1f近平面，100.f远平面

由于要把矩阵变化传给顶点着色器，所以需要修改顶点着色器使其能够接受矩阵运算。
在顶点着色器中声明一个uniform变换矩阵然后将它乘以顶点坐标：

#version 330 core
layout (location = 0) in vec3 aPos;
...
uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;

void main()
{
    // 注意乘法要从右向左读
    gl_Position = projection * view * model * vec4(aPos, 1.0);
    ...
}

我们还应该将矩阵传入着色器（这通常在每次的渲染迭代中进行，因为变换矩阵会经常变动）

int modelLoc = glGetUniformLocation(ourShader.ID, "model"));
glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
... // 观察矩阵和投影矩阵与之类似

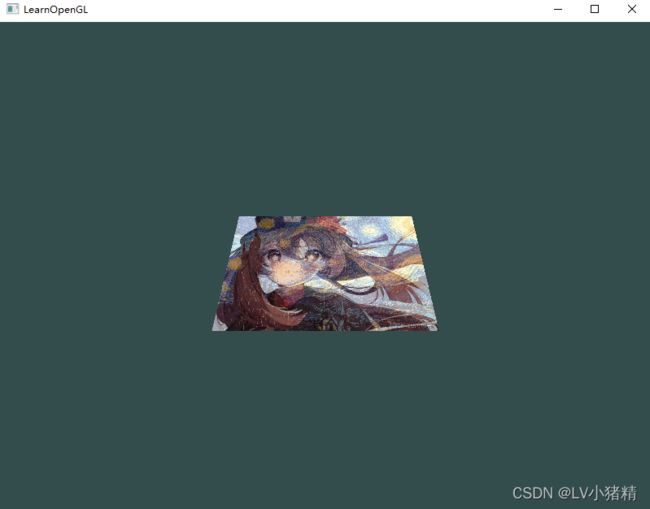
得到的结果如图所示：

---

3. 渲染部分代码

while (!glfwWindowShouldClose(window))
    {
        // input
        // -----
        processInput(window);

        // render
        // ------
        glClearColor(0.2f, 0.3f, 0.3f, 1.0f);
        glClear(GL_COLOR_BUFFER_BIT);

        // bind textures on corresponding texture units
        glActiveTexture(GL_TEXTURE0);
        glBindTexture(GL_TEXTURE_2D, texture1);
        glActiveTexture(GL_TEXTURE1);
        glBindTexture(GL_TEXTURE_2D, texture2);
  
        // activate shader
        ourShader.use();
      
        // create transformations
        glm::mat4 model         = glm::mat4(1.0f); // make sure to initialize matrix to identity matrix first
        glm::mat4 view          = glm::mat4(1.0f);
        glm::mat4 projection    = glm::mat4(1.0f);
        
        model = glm::rotate(model, glm::radians(-55.0f), glm::vec3(1.0f, 0.0f, 0.0f));
        view  = glm::translate(view, glm::vec3(0.0f, 0.0f, -3.0f));
        projection = glm::perspective(glm::radians(45.0f), (float)SCR_WIDTH / (float)SCR_HEIGHT, 0.1f, 100.0f);
        // retrieve the matrix uniform locations
        unsigned int modelLoc = glGetUniformLocation(ourShader.ID, "model");
        unsigned int viewLoc  = glGetUniformLocation(ourShader.ID, "view");
        // pass them to the shaders (3 different ways)
        glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
        glUniformMatrix4fv(viewLoc, 1, GL_FALSE, &view[0][0]);
        // note: currently we set the projection matrix each frame, but since the projection matrix rarely changes it's often best practice to set it outside the main loop only once.
        ourShader.setMat4("projection", projection);

        // render container
        glBindVertexArray(VAO);
        glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_INT, 0);

        // glfw: swap buffers and poll IO events (keys pressed/released, mouse moved etc.)
        // -------------------------------------------------------------------------------
        glfwSwapBuffers(window);
        glfwPollEvents();
    }

    // optional: de-allocate all resources once they've outlived their purpose:
    // ------------------------------------------------------------------------
    glDeleteVertexArrays(1, &VAO);
    glDeleteBuffers(1, &VBO);
    glDeleteBuffers(1, &EBO);

    // glfw: terminate, clearing all previously allocated GLFW resources.
    // ------------------------------------------------------------------
    glfwTerminate();
    return 0;
}