遗传算法学习笔记
0 参考资料
[1] 智能优化算法及其MATLAB实例(第2版),包子阳等.
链接: https://pan.baidu.com/s/1hXGvsEJfP4nBFpkaQ-zxIA 提取码: j9qb
[2] 如何理解遗传算法中的编码与解码?以二进制编码为例_雨化于画-CSDN博客
[3] 遗传算法解决TSP问题(Pyhton代码)_springtostring的博客-CSDN博客_遗传算法求解tsp问题python
[4] 禁忌搜索算法学习笔记_liuqihang11的博客-CSDN博客
1 引言
遗传算法(Genetic Algorithm,GA)是模拟生物在自然环境中的遗传和进化的过程而形成的自适应全局优化搜索算法。它借用了生物遗传学的观点,通过自然选择、遗传和变异等作用机制,实现各个个体适应性的提高。在20世纪60年代,美国的J. H. Holland教授在进行自然和人工自适应系统的研究时提出遗传算法的雏形,到了80年代, D. E. Goldberg在前人的一系列研究工作的基础上归纳总结而成了较为完备的遗传算法理论。
遗传算法借鉴了达尔文的进化论和孟德尔的遗传学说。遗传算法根据每一代个体在问题域中的适应度值,从孟德尔遗传学中借鉴来的变异、交叉等再造方法,以及从达尔文进化理论借鉴而来的优胜劣汰法则l来产生新一代种群。新一代种群中的个体比上一代种群的个体在整体上更能适应环境。
2 遗传算法理论
2.1遗传算法的生物学基础
染色体主要由DNA和蛋白质组成,而DNA是具有遗传效应的基因片段。
父代通过染色体的复制重组将其特性赋予给子代。在染色体复制重组的遗传过程中,其基因片段存在小概率性的变异交叉现象。另外,在子代的任何生命过程中也存在这种现象。生物通过染色体的复制重组将遗传信息传递给子代,这使得生物的性状可以维持一定程度的稳定;而基因片段的交叉变异使得生物产生新的遗传信息,进而产生新的形状、乃至形成新的物种,这推动了生物的进化。生物体内染色体的复制重组过程以及基因片段的交叉变异操作,使得整个生物群体的进化过程在不失多样性的同时却又能维持其相对稳定。
人们正是通过环境对个体的选择、基因的交叉和变异这些生物演化迭代过程的模仿,才提出了强鲁棒性和自适应性的遗传算法。生物遗传和进化的规律有:
(1)生物的所有遗传信息都包含在其染色体中,染色体决定了生物的性状。染色体是由基因及其有规律的排列所构成的;
(2)生物的繁殖过程是由其基因的复制过程来完成的。同源染色体的交叉或变异会产生新的物种,使生物呈现新的性状;
(3)对环境适应能力强的基因或染色体,比适应能力差的基因或染色体有更多的机会遗传到下一代。
2.2遗传算法基本概念
(1)种群和个体
种群是生物进化过程中的一个集团,表示可行解集。个体是组成群体的单个生物体,表示可行解。
(2)遗传编码
遗传编码将优化变量转化为基因的组合表示形式。优化变量的编码机制有二进制编码、十进制编码(实数编码)等。
(3)染色体和基因
染色体是包含生物体所有遗传信息的化合物,表示可行解的编码。基因是控制生物体某种性状(即遗传信息)的基本单位,表示可行解编码的分量。
(4)适应度
适应度即生物群体中个体适应生存环境的能力。在遗传算法中,用来评价个体优劣的数学函数,称为个体的适应度函数。适应度函数是选择操作的依据,适应度函数设计直接影响到遗传算法的性能。适应度函数通常就是目标函数本身或者简单映射。
(5)遗传操作
遗传操作是优选强势个体的“选择”、个体间交换基因产生新个体的“交叉”、个体基因信息突变而产生新个体的“变异”这三种变换的统称。生物的遗传主要是通过选择、交叉、变异三个过程把当前父代群体的遗传信息遗传到下一代(子代)成员。与此对应,遗传算法中最优解的搜索过程也模仿生物的这个进化过程,使用所谓的遗传算子来实现,即选择算子、交叉算子、变异算子。
(6)选择算子
根据个体的适应度,按照一定的规则或方法,从第t代群体P(t)中选择出一些优良的个体遗传到下一代群体P( t+1)中。比较常用的选择方法有:结合适应度函数轮盘赌、末尾淘汰法等。
(7)交叉算子
将群体P(t)中选中的各个个体随机搭配,对每一对个体,以某一概率(交叉概率Pt)交换它们之间的部分染色体。通过交叉,遗传算法的全局搜索能力得以飞跃提高。
交叉操作一般分为以下几个步骤:首先,从存活的父代中随机取出要交配的一对个体;然后随机选择个体基因编码上的子区间作为交叉位置;最后,根据交叉概率Pt实施交叉操作,从而形成一对新的个体。
(8)变异算子
对群体中的每个个体,以某一概率(变异概率Pm)将某一个或某一些基因座上的基因值改变为其他的等位基因值。
3 遗传算法特点
遗传算法是模拟生物在自然环境中的遗传和进化的过程而形成的一种并行、高效、全局搜索的方法,它主要有以下特点:
(1) 遗传算法以决策变量的编码作为运算对象。这种对决策变量的编码处理方式,使得在优化计算过程中可以借鉴生物学中染色体和基因等概念,模仿自然界中生物的遗传和进化等的机理,方便地应用遗传操作算子。
(2) 遗传算法直接以目标函数值作为搜索信息。它仅使用由目标函数值变换来的适应度函数值就可确定进一步的搜索方向和搜索范围,而不需要目标函数的导数值等其他一些辅助信息。这一特点使得其应用范围十分广泛。
(3) 遗传算法同时使用多个搜索点的搜索信息。遗传算法对最优解的搜索过程,是从一个由很多个体所组成的初始群体开始的,而不是从单一的个体开始的。 这一特点使得遗传算法具有较为强大的并行运算以及全局搜索能力。
(4) 遗传算法是一种基于概率的搜索技术。遗传算法属于自适应概率搜索技术,其选择、交叉、变异等运算都是以一种概率的方式来进行的,从而增加了其搜索过程的灵活性。
遗传算法的主要本质特征在于群体搜索策略和简单的遗传算子,这些特征使得遗传算法获得了搜寻解的全局性、问题域的独立性、信息处理的并行性、应用的鲁棒性和操作的简明性等特点,从而成为一种具有良好适应性和可规模化的求解方法。
4 遗传算法的改进
大量的实践和研究表明,遗传算法存在局部搜索能力差和“早熟”等缺陷,不能保证算法收敛。
遗传算法的性能主要受到6个方面的影响:编码机制、选择策略、交叉算子、变异算子、特殊算子和参数设计(包括群体规模、交叉概率、变异概率)等。因此在应用遗传算法的过程中,可根据具体问题适当改进以上六个方面。
此外,遗传算法与差分进化算法、免疫算法、蚁群算法、粒子群算法、模拟退火算法、禁忌搜索算法和量子计算等结合起来所构成的各种混合遗传算法,可以综合遗传算法和其他算法的优点,提高运行效率和求解质量。
5 遗传算法流程
遗传算法的运算流程如图1所示。具体步骤如下:
(1) 初始化。设置进化代数计数器g=0,设置最大进化代数G,设置生成N个个体作为初始群体P(0)。
(2) 个体评价。计算群体P(t)中各个个体的适应度。
(3) 变异运算。将变异算子作用于群体,对选中的个体,以某一概率改变某一个或某一些基因值为其他的等位基因。
(4) 选择运算。将选择算子作用于群体,根据个体的适应度,按照一定的规则或方法,选择一些优良个体遗传到下一代群体。
(5) 交叉运算。基于(4)的选择运算后,将交叉算子作用于选择后剩下的个体。对选中的成对个体,以某一概率交换它们之间的部分染色体,产生新的个体对。群体P(t)经过选择、交叉和变异运算之后得到下一代群体P(t+1)。计算其适应度值,并根据适应度值进行排序,准备进行下一次遗传操作。另外,群体经交叉操作后个体数重新成为N。
(6) 终止条件判断:若g≤G,则g= g+1,转回到步骤(2);若g>G,则此进化过程中所得到的具有最大适应度的个体作为最优解输出,终止计算。
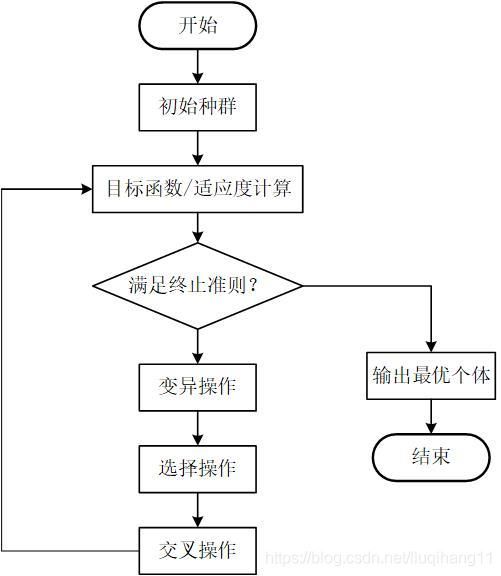 |
| 图1 遗传算法流程图 |
6 关键参数设置
(1)群体规模N
群体规模将影响遗传优化的最终结果以及遗传算法的执行效率。当群体规模N太小时,遗传优化性能一般不会太好;采用较大的群体规模可以减小遗传算法陷入局部最优解的机会,但较大的群体规模意味着计算复杂度较高。一般N取10—1000。
(2)交叉概率Pc
交叉概率Pc控制着交叉操作被使用的频度。较大的交叉概率可以增强遗传算法开辟新的搜索区域的能力,但高性能的模式遭到破坏的可能性增大;若交叉概率太低,遗传算法搜索可能陷入迟钝状态。一般Pc取0.25~1.00。
(3)变异概率Pm
变异在遗传算法中属于辅助性的搜索操作,它的主要目的是保持群体的多样性。一般低频度的变异可防止群体中重要基因的可能去失;高频度的变异将使遗传算法趋于纯粹的随机搜索。通常P取0.001~0.4。
(4)遗传运算的终止进化代数G
终止进化代数G表示遗传算法运行结束条件的一个参数,它表示遗传算法运行到指定的进化代数之后就停止运行,并将当前群体中的最佳个体作为所求问题的最优解输出。一般视具体问题而定,G的取值可在100—1000之间。
7 算法设计
7.1 编码设计
常用的编码方式有二进制编码、浮点数编码等。对于初学者而言,考虑使用二进制编码即可。
 |
| 图2 二进制编码示意图 |
图2即为一个二进制编码示意图。显然,由排列组合的方法可知,一个长度为L的二进制编码串,一共有2^L中不同的排列方式。如果使用一个二进制排列表示一个十进制数,那么共可以表示2^L个不同的十进制数。假设十进制数从0开始,则可以表示0—2^L-1个十进制整数。这就是二进制数表示十进制正整数的思路。如果要表示小数的话,比如说10.000,思路是只需要表示出10000,然后在解码时,先解码出10000,再缩小至10.000即可;如果要表负数的话,也只需要先表示成正整数,再在解码时转化为负数即可。
下面来看一个具体的例子,将[-7, 20]转化为二进制编码,精度为0.0001。
首先看需要表示的集合范围,范围内最大的数似乎是20,实则不然。我们说过,负数也是需要先转化为正整数来表示的,因此将[-7, 20]整体往右移动7个单位,得到[0, 27],最大的数其实是27。
由于需要表示的数据精度为0.0001,即需要表示出27.0000。按照之前的说法,有小数的话需要先将其转化为整数再进行表示,这里只需去掉小数点,直接扩大到270000即可。
需要表示的正整数就是0—270000,共270001个,直接利用公式2^L-1=27000,求解出L即可,解得L=18.04。求得的L便是编码长度。
注意到18.04不是整数,显然不合理,这个时候就需要向上取整,L取为19。新的问题来了,我们本来打算使用第2^L个二进制排列表示270000,基于这种想法,求得L=18.04。实际上我们使用的是L=19,也就是说270000是由2^19-1=524287表示的,而不是期望的2^18.04-1。
总结而言,编码长度L可由下式计算:
其中的[ ]表示向上取整,Up表示需要表示的数据上限,Low表示需要表示的数据下限,Accuracy表示数据精度。
基于6.1节的计算,[-7, 20]内的所有数字都可以通过一个长度为19的二进制字符串表示出来,且精度为0.0001。之后的选择、变异和交叉计算都是基于这些二进制编码。
7.2 解码设计
在选择、变异、交叉操作完成后,需要将二进制编码转化为十进制数,从而计算新的适应性函数值。若原数据集有小数或者负数的,还需要将得到的十进制整数还原为小数、负数。具体步骤为:
首先,将二进制数还原为十进制正整数,这个过程可以直接通过Python的方法int(x,2)实现(注意x必须是字符串类型)。
在使用了int(x,2)方法后,得到了[0,524287]范围内的正整数数据,然后将这些正整数统统缩小至[0,27],最后再整体往左平移7个单位就可得到[-7,20]。
总结而言,解码规则为:
![]()
其中,'x(2)' 表示字符串类型,int('x(2)' ,2)表示将字符串类型的x(2)编码转化为十进制数。
需要指出的是,TSP问题不需要编码解码操作,其城市编号就是天然的编码。
7.3 适应度函数设计
适应度函数通常就是目标函数本身或者其简单映射。比如求解最大值问题时,适应度函数可以取为目标函数的相反数,求解最小值时适应度函数可以取为目标函数本身;对于一些没有目标函数的题目,需要从问题中抽象出相应的适应度函数。比如TSP问题的适应度函数就可以取为路程的计算函数。
7.4 选择算子设计
选择算子可以使用末尾淘汰法或者轮盘赌法来设计。
末尾淘汰制就是人为设定一个选择概率Pc,适应度函数值排在前Pc的个体存活,后面的直接被淘汰。
下面再说说轮盘赌法:
轮盘赌法是遗传算法中最早提出的一种选择方法。它是一种基于比例的选择,利用各个个体适应度所占比例的大小来决定其子孙保留的可能性。若某个个体i的适应度为fi,种群大小为N,则它被选取的概率表示为:
个体适应度越大,则其被选择的机会也越大;反之亦然。对每个个体进行选择操作,需要进行多轮选择。每一轮产生一个[0,1]内的均匀随机数,将该随机数作为选择指针来确定该个体是否存留。
7.5 交叉算子的设计
将群体P(t)中选中的各个个体随机搭配,对每一对个体,以某一概率(交叉概率Pt)交换它们之间的部分染色体。
交叉操作一般分为以下几个步骤:
首先,从执行选择操作后剩余的个体中随机抽取一对需要交配的个体;
然后,对要交配的一对个体,根据其位串长度L随机选取[1,L-1]中的一个或多个整数k作为交叉位置;
最后,根据交叉概率Pt实施交叉操作,即配对个体在交叉位置处相互交换各自的部分基因,从而形成新的一对个体。
以上是一般优化问题的交叉策略,比如0-1背包问题、函数最值问题等等。
TSP问题的交叉与一般问题不同,在交叉之后还需要考虑元素重复和缺失问题。下面结合实例分析TSP问题的交叉步骤:
步骤1:随机从存活的个体中选择两个作为父代,使用父1,父2表示。
| 父1 |
 |
| 父2 |
步骤2:在步骤1得到父1和父2的基因点上随机选择交叉初始位置left(left=2),交叉基因段长度固定为length(length=3),从而确定交叉片段的终止点right=left+length(right=5,不包括right),最终得到交叉片段1和2。
 |
| 交叉片段1 |
 |
| 交叉片段2 |
步骤3:将步骤1得到的父1,父2进行如下操作: right=5及其之后的基因片段移动到最开头,得到父11和21,其余基因依次后移:
 |
| 父11 |
 |
| 父21 |
步骤4:对于步骤3得到的父11,删除其与步骤2得到的交叉片段2中相同的基因,对于步骤3得到的父21,删除其与步骤2得到的交叉片段1中相同的基因,最终得到子11和子21:
 |
| 子11 |
 |
| 子21 |
步骤5:对于步骤3得到的父11和父21,在其left=2到right=5(不包括right)的位置分别插入交叉片段2和交叉片段1,得到子12和子22:
 |
| 子12 |
 |
| 子22 |
步骤6:将子12中right=5到结尾位置的2个元素(len(子12)-right=2)替换为子11中第1个元素到第2个元素(len(子12)-right=2),将子12中第1个元素到第2个元素(left=2)替换为子11中的倒数第1到倒数第2个元素(left=2);将子22中right=5到结尾位置的共2个元素(len(子22)-right=2)替换为子21中第1个元素到第2个元素(len(子22)-right=2),将子22中第1个元素到第二个位置的元素(left=2)替换为子21中的倒数第1到倒数第2个元素(left=2)。最终得到子1代和子2代:
 |
| 子1 |
 |
| 子2 |
到此两个父代的交叉完成,得到两个子代。
步骤7:重复步骤1到步骤6的操作,直到种群中的个体数恢复为N。
7.6 变异算子的设计
变异算子的设计比较简单,对种群中所有个体按照设定的变异概率Pm进行变异即可。变异的方法通常是任选个体的两个基因位置交换:
 |
| 变异前 |
 |
| 变异后 |
图片中所示的变异位置为第一个和最后一个。
8 使用遗传算法求解函数最值实例
8.1 Python代码
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import random
import copy
# 种群数
count = 100
# 进化次数(手动输入)
itter_time = 0
# 每次最优的目标函数
result = []
# 存储历史目标函数最优
register = []
# 编码长度
code_length = 28 # 最大为10.000,精度为0.001,。2*[log2(10/0.001)],[]为向上取整
# 每一代最差的个体的目标函数值
worst_value = 0
# 设置强者的定义概率,即种群前30%为强者
retain_rate = 0.3
# 设置弱者的存活概率
random_select_rate = 0.5
# 交叉概率不单独定义,实际上通过弱者的存活概率以及强者概率可以计算出交叉概率(弱者死亡率即为交叉概率)
# 变异率
mutation_rate = 0.2
# 计算目标函数值(以此作为自然选择的依据)
def get_value(x):
temp = copy.deepcopy(x)
x = temp[:(code_length // 2)]
y = temp[(code_length // 2):-1]
x = ''.join(x)
y = ''.join(y)
x = -5 + (5 - (-5)) / (2**(code_length // 2) - 1) * int(x, 2) # 二进制转码十进制
y = -5 + (5 - (-5)) / (2**(code_length // 2) - 1) * int(y, 2)
value = -((np.cos(y**2 + x**2) - 0.1) / (1 + 0.3 * (y**2 + x**2)**2) + 3)
return value
# 初始化种群
def initialize_population():
population = []
x = []
for i in range(code_length): # 长度为code_length的二进制码
temp = random.sample([0, 1], 1)
x.append(str(temp[0]))
while (1):
if (len(population) > count):
break
else:
random.shuffle(x) # 随机生成个体
population.append(x)
return (population)
# 得到最佳结果
def get_result(population):
graded = [[get_value(x), x]
for x in population] # 第二列存储种群中的个体,第一列存储个体对应的目标函数值
graded = sorted(graded)
return graded[0][0], graded[0][1] # 返回最优的x及其对应的目标函数值
# 自然选择
def selection(population):
global worst_value
"""
选择
将目标函数值从大到小排序,选出存活的染色体
再进行随机选择,选出适应度虽然小,但是幸存下来的个体
"""
# 对目标函数值从小到大进行排序
graded = [[get_value(x), x] for x in population]
graded = [x[1] for x in sorted(graded)] # 只保留了x,目标函数值仅起到排序作用
# 选出适应性强的染色体
retain_length = int(len(graded) * retain_rate)
worst_value = get_value(graded[-1])
parents = graded[:retain_length] # 0-retain_length长度的子代被选择
# 选出适应性不强,但是幸存的染色体
for chromosome in graded[retain_length:]: # 剩下的个体以50%的概率存活
if random.random() < random_select_rate:
parents.append(chromosome)
return parents
# 变异
def mutation(population): # population 是一个M*N的列表,M为种群数目,N为每个个体的二进制编码
mutation_index_x = [x for x in range(0, (len(population[0]) // 2))]
mutation_index_y = [
x for x in range((len(population[0]) // 2), len(population[0]))
]
for i in range(1, len(population)): # 最优的不变异
temp_population = copy.copy(population[i])
if random.random() < mutation_rate:
mutation_position_x = random.sample(mutation_index_x, 2)
mutation_position_y = random.sample(mutation_index_y, 2)
temp_x = population[i][mutation_position_x[0]]
temp_y = population[i][mutation_position_y[0]]
population[i][mutation_position_x[0]] = population[i][
mutation_position_x[1]]
population[i][mutation_position_y[0]] = population[i][
mutation_position_y[1]]
population[i][mutation_position_x[1]] = temp_x
population[i][mutation_position_y[1]] = temp_y
if (get_value(temp_population) < get_value(
population[i])): # 变异接受法则
population[i] = temp_population
return population
# 交叉繁殖方法,自然选择后再交叉
def crossover(parents):
global worst_value
# 需要交叉生成的子代个数,以此保证种群稳定
target_count = count - len(parents)
# 孩子列表
children = []
while len(children) < target_count:
male_index = random.randint(0,
len(parents) - 1) # 存活的个体进行交换,获取需要交换的父母索引
female_index = random.randint(0, len(parents) - 1)
if male_index != female_index:
male = parents[male_index]
child1 = copy.copy(male)
female = parents[female_index]
child2 = copy.copy(female)
left_x = random.randint(0,
len(male) // 2 -
5) # 需要交换的片段左起点,包含了下界0和上界len
left_y = random.randint(len(male) // 2,
len(male) - 5) # 注意这里当基因片段过少是会报错
for i in range(4): # 4表示从left开始的4个基因片段需要交换
child1[i + left_x] = female[i + left_x]
child2[i + left_x] = male[i + left_x]
child1[i + left_y] = female[i + left_y]
child2[i + left_y] = male[i + left_y]
children.append(child1)
children.append(child2)
return children
def draw():
global register
global itter_time
# 绘制函数图像
fig = plt.figure()
ax = Axes3D(fig, auto_add_to_figure=False)
fig.add_axes(ax) # auto_add_to_figure=False和fig.add_axes(ax)防止Axes3D报警
# 使用np.linspace定义 x:范围(-5,5);个数为200
x = np.linspace(-5, 5, 200)
# 定义 y:范围(-5,5);个数为200
y = np.linspace(-5, 5, 200)
# 创建x-y平面网络
X, Y = np.meshgrid(x, y)
Z = (np.cos(Y**2 + X**2) - 0.1) / (1 + 0.3 * (Y**2 + X**2)**2) + 3
# plt.xlabel('x')
# plt.ylabel('y')
# 将函数显示为3d rstride 和 cstride 代表 row(行)和column(列)的跨度 get_cmap为色图分类
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
plt.savefig('GA.8.2.1.png', dpi=500)
plt.pause(3)
# 绘制迭代次数图
plt.figure(tight_layout=True)
x = list(range(len(register)))
y = register
plt.plot(x, y, 'g-')
plt.title('ymax= {}'.format(round(register[-1], 4)) +
'\ntotal interations:' + str(itter_time))
plt.xlabel('interation')
plt.ylabel('y')
plt.savefig('GA.8.2.2.png', dpi=500)
plt.pause(3)
def solve():
global register
global itter_time
population = initialize_population() # 种群初始化
i = 0
result, best_x = get_result( # 获取初始种群
population) # 使用best_x和result接收x以及目标函数值
register.append(result)
itter_time = int(input('输入进化次数: '))
while i < itter_time: # itter_time为进化次数
# 变异操作, 先变异后选择
population = mutation(population)
# 选择繁殖个体群
parents = selection(population)
# 交叉繁殖
children = crossover(parents)
# 更新种群
population = parents + children
result, best_x = get_result(population)
register.append(-result)
i = i + 1
temp = copy.copy(best_x)
best_x = temp[:code_length // 2]
best_y = temp[code_length // 2:]
best_x = ''.join(best_x)
best_y = ''.join(best_y)
best_x = -5 + (5 - (-5)) / (2**(code_length // 2) - 1) * int(best_x,
2) # 二进制转码十进制
best_y = -5 + (5 - (-5)) / (2**(code_length // 2) - 1) * int(best_y, 2)
print(round(best_x, 3))
print(round(best_y, 3))
print(round(-result, 4))
draw()
if __name__ == "__main__":
solve()
8.2 结果展示
9 使用遗传算法求解0-1背包问题实例
9.1 Python代码
import matplotlib.pyplot as plt
import random
import copy
# 种群数
count = 100
# 进化次数(手动输入)
itter_time = 0
# 每次最优的目标函数
result = []
# 物品体积
column = [95, 75, 23, 73, 50, 22, 6, 57, 89, 98]
# 物品价值
value = [89, 59, 19, 43, 100, 72, 44, 16, 7, 64]
# 背包容量
capacity = 300
# 不合格的存放方式
forbidden_x = []
# 存储历史目标函数最优
register = []
# 编码长度
code_length = 10 # 总共十个物品
# 每一代最差的个体的目标函数值
worst_value = 0
# 设置强者的定义概率,即种群前30%为强者
retain_rate = 0.3
# 设置弱者的存活概率
random_select_rate = 0.5
# 交叉概率不单独定义,实际上通过弱者的存活概率以及强者概率可以计算出交叉概率(弱者死亡率即为交叉概率)
# 变异率
mutation_rate = 0.05
# 计算目标函数值(以此作为自然选择的依据)
def get_value(x):
global value
global forbidden_x
total_value = 0
for i in range(len(value)):
total_value -= x[i] * value[i] # 使用-=是因为求取最大值,需要使用目标函数的相反数
if (x in forbidden_x):
total_value = 0 # 不合理的存放方式的价值直接设置为0
return total_value
# 计算总重量
def get_column(x):
global column
total_column = 0
for i in range(len(x)):
total_column += x[i] * column[i]
return total_column
# 初始化种群
def initialize_population():
global code_length
global count
population = []
x = []
for i in range(code_length): # 长度为code_length的二进制码
temp = random.sample([0, 1], 1) # 1表示装入背包,0表示不装入
x.append(temp[0])
while (1):
if (len(population) > count):
break
else:
random.shuffle(x) # 随机生成个体
population.append(x)
return (population)
# 得到最佳结果
def get_result(population):
graded = [[get_value(x), get_column(x), x]
for x in population] # 第二列存储种群中的个体,第一列存储个体对应的目标函数值
graded = sorted(graded)
return graded[0][0], graded[0][1], graded[0][2] # 返回最优的x,其对应的总重量及目标函数值
# 自然选择
def selection(population):
global worst_value
global capacity
global retain_rate
global random_select_rate
"""
选择
先对适应度从大到小排序,选出存活的染色体
再进行随机选择,选出适应度虽然小,但是幸存下来的个体
"""
# 对总价值从小到大进行排序
graded = [[get_value(x), get_column(x), x] for x in population]
graded = sorted(graded, key=lambda x: (x[1]), reverse=True)
for i in range(len(graded)):
if (graded[i][1] < capacity):
break
else:
forbidden_x.append(graded[i][2]) # 记录不合理的存放方法
graded = [x[2] for x in sorted(graded)] # 只保留了x,目标函数值仅起到排序作用
# 选出适应性强的染色体
retain_length = int(len(graded) * retain_rate)
worst_value = get_value(graded[-1])
parents = graded[:retain_length] # 0-retain_length长度的子代被选择
# 选出适应性不强,但是幸存的染色体
for chromosome in graded[retain_length:]: # 剩下的个体以50%的概率存活
if random.random() < random_select_rate:
parents.append(chromosome)
return parents
# 变异
def mutation(population): # population 是一个M*N的列表,M为种群数目,N为每个个体的二进制编码
global mutation_rate
global capacity
mutation_index = [x for x in range(len(population[0]))]
for i in range(1, len(population)): # 最优的不变异
temp_popolation = population[i]
if random.random() < mutation_rate:
k = random.sample(mutation_index, 2)
temp = population[i][k[0]]
population[i][k[0]] = population[i][k[1]]
population[i][k[1]] = temp
if (get_value(population[i]) > worst_value
or get_column(population[i]) > capacity): # 接受准则
population[i] = temp_popolation
return population
# 交叉繁殖方法,自然选择后再交叉
def crossover(parents):
global worst_value
global count
# 需要交叉生成的子代个数,以此保证种群稳定
target_count = count - len(parents)
# 孩子列表
children = []
while len(children) < target_count:
male_index = random.randint(0,
len(parents) - 1) # 存活的个体进行交换,获取需要交换的父母索引
female_index = random.randint(0, len(parents) - 1)
if male_index != female_index:
male = parents[male_index]
child1 = copy.copy(male)
female = parents[female_index]
child2 = copy.copy(female)
left = random.randint(0, len(male) - 3) # 需要交换的片段左起点,包含了下界0和上界len
for i in range(2): # 2表示从left开始的2个基因片段需要交换
child1[i + left] = female[i + left]
child2[i + left] = male[i + left]
children.append(child1)
children.append(child2)
return children
def draw():
global register
global itter_time
# 绘制迭代次数图
plt.figure(tight_layout=True)
x = list(range(len(register)))
y = register
plt.plot(x, y, 'g-')
plt.title('Value max= {}'.format(round(register[-1], 4)) +
'\ntotal interations:' + str(itter_time))
plt.xlabel('interation')
plt.ylabel('Total Value')
plt.savefig('GA.2.4.png', dpi=500)
plt.show()
def solve():
global register
global itter_time
population = initialize_population() # 种群初始化
i = 0
best_result, best_column, best_x = get_result( # 获取初始种群
population) # 使用best_x和result接收x以及目标函数值
register.append(best_result)
itter_time = int(input('输入进化次数: '))
while i < itter_time: # itter_time为进化次数
# 变异操作, 先变异后选择
population = mutation(population)
# 选择繁殖个体群
parents = selection(population)
# 交叉繁殖
children = crossover(parents)
# 更新种群
population = parents + children
best_result, best_column, best_x = get_result(population)
register.append(-best_result)
i = i + 1
for i in range(len(best_x)):
best_x[i] = str(best_x[i])
best_x = ''.join(best_x)
print(best_x)
print(best_column)
print(-best_result)
draw()
if __name__ == "__main__":
solve()
9.2 结果展示
10 使用遗传算法求解TSP问题实例
10.1 Python代码
此部分代码及数据参考了'遗传算法解决TSP问题(Pyhton代码)_springtostring的博客-CSDN博客_遗传算法求解tsp问题python’。
import numpy as np
import matplotlib.pyplot as plt
import random
import copy
import matplotlib.animation as animation
# 种群数
count = 1000
# 进化次数(手动输入)
itter_time = 0
# 存储路径
result_path = []
# 存储所有路径
all_path = []
# 存储历史距离
register = []
# 出发城市
origin = 0
# 城市信息(读取)
city_x_condition = []
city_y_condition = []
# 城市数目
city_count = len(city_x_condition)
# 生成一个n*n的array存储各个城市到其他城市的路程
Distance = [np.zeros([city_count, city_count])]
# 记录每次迭代的最优距离
distance = 0
# 每一代最差的个体的距离
worst_distance = 0
# 设置强者的定义概率,即种群前20%为强者
retain_rate = 0.3
# 设置弱者的存活概率
random_select_rate = 0.5
# 交叉概率不单独定义,实际上通过弱者的存活概率以及强者概率可以计算出交叉概率(弱者死亡率即为交叉概率)
# 变异率
mutation_rate = 0.6
# 载入数据
def get_data():
global city_x_condition
global city_y_condition
file_name = 'GA TSP data.txt'
with open(file_name, 'r', encoding='utf_8') as f:
lines = f.readlines() # 按行读取
for line in lines:
line = line.split('\n')[0] # 每行以换行符分割
line = line.split(',') # 以逗号作为列分割
city_x_condition.append(float(line[1])) # 存储第二列数据第三列数据作为x,y坐标
city_y_condition.append(float(line[2]))
# 距离矩阵
def distance_matrix():
global city_x_condition
global city_y_condition
global city_count
global Distance
city_count = len(city_x_condition)
Distance = np.zeros([city_count, city_count])
for i in range(city_count):
for j in range(city_count):
x = pow(city_x_condition[i] - city_x_condition[j], 2)
y = pow(city_y_condition[i] - city_y_condition[j], 2)
Distance[i][j] = pow(x + y, 0.5)
# 计算每个可能的总距离
def get_total_distance(x): # x为一个不包含出发城市的数组
total_distance = 0
total_distance += Distance[origin][x[0]] # 从第一个城市出发到第二个城市
for i in range(len(x)):
if i == len(x) - 1:
total_distance += Distance[origin][x[i]] # 最后需要从最后一个城市回到出发点
else:
total_distance += Distance[x[i]][x[i + 1]]
return total_distance
# 初始化种群
def initialize_population():
global origin
global city_count
population = [] # 存储种群个体(实际就是不同的城市路径顺序编号)
# 随机设置起点
index = [i for i in range(city_count)]
origin = random.sample(index, 1)
origin = origin[0]
index.remove(origin) # 移除起点
while (1):
if (len(population) > count):
break
else:
x = copy.copy(index)
random.shuffle(x) # 随机生成个体
population.append(x)
return (population)
# 得到最佳结果
def get_result(population):
graded = [[get_total_distance(x), x]
for x in population] # 第二列存储种群中的个体,第一列存储个体对应的目标函数值
graded = sorted(graded)
return graded[0][0], graded[0][1] # 返回最优的路径及其对应的目标函数值
# 自然选择
def selection(population):
global worst_distance
"""
选择
先对适应度从大到小排序,选出存活的染色体
再进行随机选择,选出适应度虽然小,但是幸存下来的个体
"""
# 对总距离从小到大进行排序
graded = [[get_total_distance(x), x] for x in population]
graded = [x[1] for x in sorted(graded)] # 只保留了路径x,路程distance仅起到排序作用
# 选出适应性强的染色体
retain_length = int(len(graded) * retain_rate)
worst_distance = get_total_distance(graded[-1])
parents = graded[:retain_length] # 0-retain_length长度的子代被选择
# 选出适应性不强,但是幸存的染色体
for chromosome in graded[retain_length:]: # 剩下的个体以50%的概率存活
if random.random() < random_select_rate:
parents.append(chromosome)
return parents
# 变异
def mutation(population): # population 是一个M*N的列表,M为种群数目,N为城市数目
mutation_index = [x for x in range(len(population[0]))]
for i in range(1, len(population)): # 最优的不变异
temp_population = copy.copy(population[i])
if random.random() < mutation_rate:
k = random.sample(mutation_index, 2)
temp = population[i][k[0]]
population[i][k[0]] = population[i][k[1]]
population[i][k[1]] = temp
if (get_total_distance(temp_population) < get_total_distance(
population[i])): # 接受法则
population[i] = temp_population
return population
# 交叉繁殖方法1,自然选择后再交叉
def crossover(parents):
global worst_distance
# 需要交叉生成的子代个数,以此保证种群稳定
target_count = count - len(parents)
# 孩子列表
children = []
while len(children) < target_count:
male_index = random.randint(0,
len(parents) - 1) # 存活的个体进行交换,获取需要交换的父母索引
female_index = random.randint(0, len(parents) - 1)
if male_index != female_index:
male = parents[male_index]
female = parents[female_index]
left = random.randint(0, len(male) - 3) # 需要交换的片段左起点,包含了下界0和上界len
right = left + 2 # 需要交换的片段右终点,仅仅只交换两个位置
gene1 = male[left:right] # 交叉片段
gene2 = female[left:right]
child1_c = male[right:] + male[:right] # 从下角标right开始左右交换了位置
child2_c = female[right:] + female[:right]
child1 = copy.copy(child1_c)
child2 = copy.copy(child2_c)
for o in gene2:
child1_c.remove(o) # 插入前删除male中与将要从female插入的片段中重复的部分
for o in gene1:
child2_c.remove(o) # 插入前删除female中与将要从male插入的片段中重复的部分
child1[left:right] = gene2 # 插入片段
child2[left:right] = gene1 # 插入片段
child1[right:] = child1_c[0:len(child1) - right] # 补全右边
child1[:left] = child1_c[len(child1) - right:] # 补全左边
child2[right:] = child2_c[0:len(child1) - right]
child2[:left] = child2_c[len(child1) - right:]
if (get_total_distance(child1) < 1.1*worst_distance
or get_total_distance(child2) < 1.1*worst_distance): # 接受法则
children.append(child1)
children.append(child2)
return children
def draw():
global distance
global register
global all_path
global result_path
global itter_time
# 绘制最终结果图
X = []
Y = []
for i in range(len(result_path)):
index = result_path[i]
X.append(city_x_condition[index])
Y.append(city_y_condition[index])
plt.figure(tight_layout=True)
plt.xlim(85, 130) # 限定横轴的范围
plt.ylim(15, 50) # 限定纵轴的范围
plt.plot(X, Y, marker='o', mec='r', mfc='w')
plt.margins(0)
plt.subplots_adjust(bottom=0.15)
plt.xlabel(u"x") # X轴标签
plt.ylabel(u"y") # Y轴标签
plt.title("TSP Solution\n" + 'ymin= {}'.format(distance) +
'\ntotal interations:' + str(itter_time)) # 标题
plt.savefig('GA.1.png', dpi=500)
plt.pause(4)
plt.close()
# 绘制迭代次数图
plt.figure(tight_layout=True)
x = list(range(len(register)))
y = register
plt.plot(x, y, 'g-')
plt.title('ymin= {}'.format(distance) + ' km' + '\ntotal interations:' +
str(itter_time))
plt.xlabel('interation')
plt.ylabel('distance')
plt.savefig('GA.2.png', dpi=500)
plt.pause(4)
# 绘制迭代动图
X = []
Y = []
for j in range(len(all_path)):
x = []
y = []
for i in range(len(result_path)):
index = all_path[j][i]
x.append(city_x_condition[index])
y.append(city_y_condition[index])
X.append(x)
Y.append(y)
fig3 = plt.figure(tight_layout=True)
plt.xlim(85, 130) # 限定横轴的范围
plt.ylim(15, 50) # 限定纵轴的范围
line, = plt.plot(X[0], Y[0], marker='o', mec='r', mfc='w')
plt.margins(0)
plt.subplots_adjust(bottom=0.15)
def update_scatter(num):
plt.title("TSP Solution\n" + 'ymin= {}'.format(register[num]) + ' km' +
'\niter = ' + str((num))) # 标题
line.set_data(X[num], Y[num])
return line,
ani = animation.FuncAnimation(
fig3,
update_scatter,
np.arange(0, len(all_path), int(0.02 * len(all_path))),
blit=True,
interval=100,
)
ani.save('GA.3.gif', writer='pillow')
def solve():
global origin
global result_path
global distance
global register
global all_path
global itter_time
get_data() # 读取数据
distance_matrix()
population = initialize_population() # 种群初始化
i = 0
distance, result_path = get_result( # 获取初始种群
population) # 使用distance和result_path接收函数返回的路程以及路径
temp = [origin] + result_path + [origin]
all_path.append(temp)
register.append(distance)
itter_time = int(input('输入进化次数: '))
while i < itter_time: # itter_time为进化次数
# 变异操作, 先变异后选择
population = mutation(population)
# 选择繁殖个体群
parents = selection(population)
# 交叉繁殖
children = crossover(parents)
# 更新种群
population = parents + children
distance, result_path = get_result(population)
temp = [origin] + result_path + [origin]
all_path.append(temp)
register.append(distance)
i = i + 1
print(distance)
result_path = all_path[-1]
print(result_path)
draw()
if __name__ == "__main__":
solve()
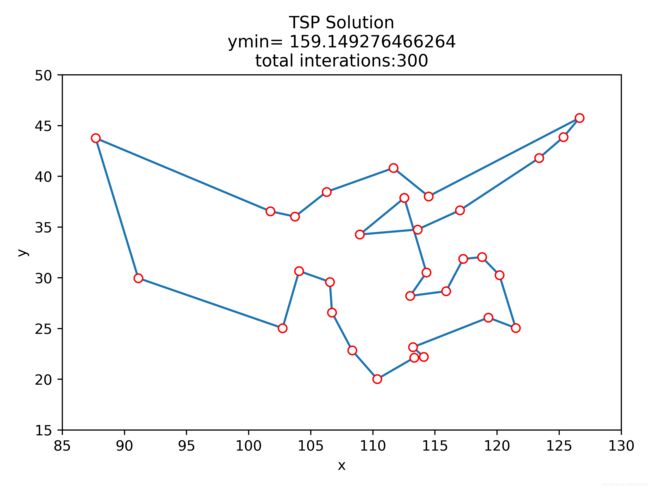
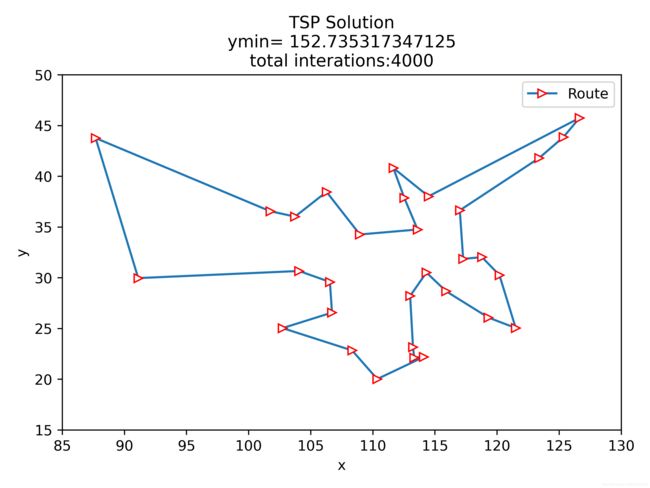
10.2 结果展示
使用遗传算法求解TSP的效果并不理想,很容易陷入局部最优。通过增大变异率Pm以及种群数量N可以在一定程度上改善局部最优困境,但其优化结果与其他优化方法得到的结果相比仍然不太乐观。以下是使用禁忌搜索求解相同问题得到的结果图:
禁忌搜索的源代码可见'禁忌搜索算法学习笔记_liuqihang11的博客-CSDN博客',稍作修改便可使用。