Self-Attention原理
Self-Attention原理
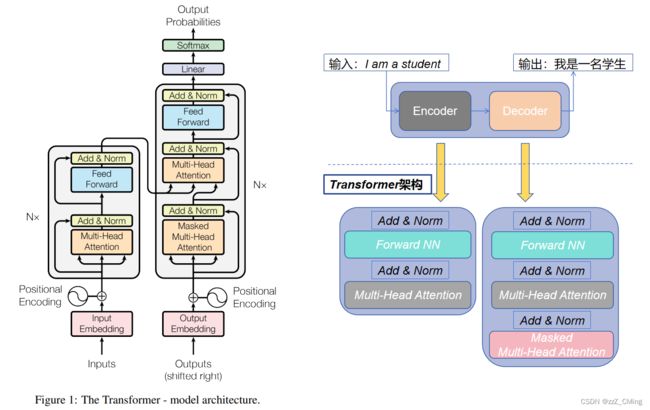
论文《Attention Is All You Need》中公布的Transformer示意图整体还是Encoder-Decoder结构。其中Multi-Head Attention(多头注意力)层中的Self-Attention(自注意力)机制是Transformer 架构中重要的部分。
- 左侧是Encoder过程,包含一个Multi-Head Attention(多头注意力)层,
- 右侧是Decoder过程,包含两个Multi-Head Attention(多头注意力)层,其中一个是用在Masked中。
- Add & Norm 层:Add 表示残差连接 (Residual Connection) 用于防止网络退化,Norm表示 Layer Normalization,用于对每一层的激活值进行归一化;
- Feed Forward层:前馈网络层,包含两个全连接层,第一层激活函数为ReLU函数,第二层无激活函数,表达式为: F N N ( x ) = m a x ( 0 , x W 1 + b 1 ) W 2 + b 2 FNN(x)=max(0,xW_1 + b_1)W_2 + b_2 FNN(x)=max(0,xW1+b1)W2+b2
1、Attention的计算公式
右边的 Multi-Head Attention (多头注意力)层包含了多个左边Self-Attention 的计算过程。
![]()
先看左边 Self-Attention的计算图,计算公式为: A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q ⋅ K T d k ) V Attention(Q,K,V)=softmax(\frac{Q·K^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dkQ⋅KT)V(Q与K的转置做内积,再除以K的维度,经过softmax归一化,最后与V相乘。Q,K,V 皆为矩阵)。经过Self-Attention结构,最后得到的输出被叫做注意力分数。
- Q:querys,查询矩阵
- K:keys,键值矩阵
- V:values,数值矩阵
实际中,Self-Attention接收的输入分两种——词空间矩阵X(n,d),或者上一个Encoder/Decoder block的输出,这两种方式传递的都是词向量 X X X。而 Q, K, V 矩阵都是词向量 X X X进行线性变换后得到的,本质上只是词向量 X X X的变相表达。
2、Q,K,V 矩阵的由来
W Q 、 W K 、 W V W^Q、W^K、W^V WQ、WK、WV就是词向量 X X X做线性变换所用到的参数,它们随机生成并参与梯度训练。
![]()
既然Q,K,V 等价于词向量 X X X,那为什么不直接使用词向量 X X X参与后续运算呢?求取Q,K,V矩阵的意义是什么呢?
答:是为了提升模型的拟合能力。矩阵 W Q 、 W K 、 W V W^Q、W^K、W^V WQ、WK、WV是可以变化的,能逼近词向量 X X X在某一维度上的边界,相当于是求取词向量 X X X的“三视图”。
3、注意力分数的意义
上文已经知道注意力分数 A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q ⋅ K T d k ) V Attention(Q,K,V)=softmax(\frac{Q·K^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dkQ⋅KT)V,其中Q, K, V 是词向量 X X X的线性变换,线性变换只改变外在,不改变实质,所以极限情况可以使Q = K = V = X ,那么计算公式就可以简化为: A t t e n t i o n ( X ) = s o f t m a x ( X ⋅ X T ) X Attention(X)=softmax(X·X^T)X Attention(X)=softmax(X⋅XT)X。这样就方便研究注意力分数的实际意义了。
①、 X ⋅ X T X·X^T X⋅XT的意义,一个矩阵乘以它自身的转置,有什么意义?会得到什么结果?
矩阵是由一个个向量组成,一个矩阵乘以它自身的转置,可以看成其向量分别与其他向量计算内积,内积的几何意义是:表征两个向量的夹角,表征一个向量在另一个向量上的投影大小。我们知道:
- 内积越大,说明投影越大,两者相关性越强;
- 内积等于0,说明两者的向量夹角等于九十度,这两个向量线性无关,完全没有相关性。
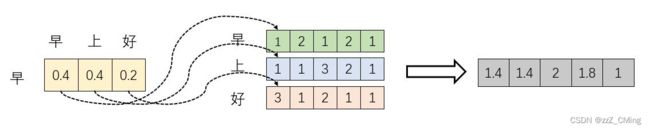
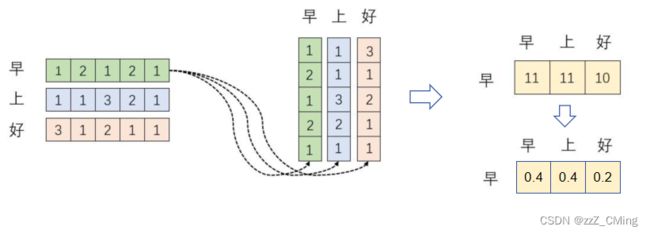
下图模拟 X ⋅ X T X·X^T X⋅XT的计算过程:
词向量 “早(12121)” 分别与 “早、上、好” 做内积,得到一个新向量(11,11,10),新向量数值代表相关性大小;
所以:词向量在高维空间做内积得到投影值,投影值越大,说明这两个词的相关性越强,进而在一定程度上说明,在关注词A的同时,也应当给予词B更多的关注;
②、 s o f t m a x ( X ⋅ X T ) softmax(X·X^T) softmax(X⋅XT)的意义
Self-Attention 翻译为“自注意力”,其本质是依赖词空间 X ( n , d ) X(n,d) X(n,d)让每个词向量 X i X_i Xi都能由其他词向量 X n X_n Xn联合表示,联合表示的方法就是进行加权求和,这个“权重”就是上面所求的相关性。而 s o f t m a x ( ) softmax() softmax()的意义就是将相关性数值转化成分式表达。
例如下图:
当我们关注"早"这个字的时候,我们应当分配 0.4 的注意力给它本身,0.4 的注意力给"上",0.2 的注意力给"好"。
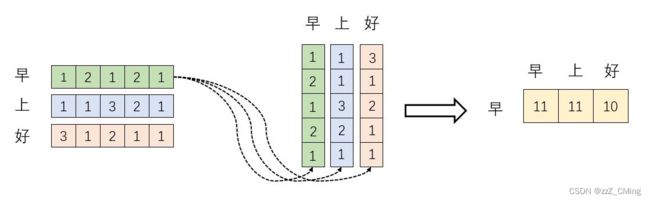
③、 s o f t m a x ( X ⋅ X T ) X softmax(X·X^T)X softmax(X⋅XT)X的意义
上面的计算,已经求取了联合表示的参数,最后再乘上矩阵X,就完成了所有词向量 X X X经过注意力机制加权后,在词空间上的联合表示方法。
例如下图:词向量 “早(12121)” 的权重是 ( 0.4 , 0.4 , 0.2 ) (0.4,0.4,0.2) (0.4,0.4,0.2),与矩阵的每一列相乘,实际是将词向量"早(12121)“每一位进行转化,每一位都用"早、上、好” 联合表示,进而将 "早(12121)"转化成新向量,新向量维度不变,将孤立的词转化成“你中有我,我中有你”的联合表示形式。这个联合表示形式就是Self-Attention的输出,也被叫做注意力分数。
总结:
- X ⋅ X T X·X^T X⋅XT的意义:词空间中,任意两个词向量的相关性大小;
- s o f t m a x ( X ⋅ X T ) softmax(X·X^T) softmax(X⋅XT)的意义:将相关性转化成联合参数;
- s o f t m a x ( X ⋅ X T ) X softmax(X·X^T)X softmax(X⋅XT)X的意义:用联合参数,将每一个词向量都转为联合表达的形式。这就是注意力分数的意义。
补充: d k \sqrt{d_k} dk的意义
![]()
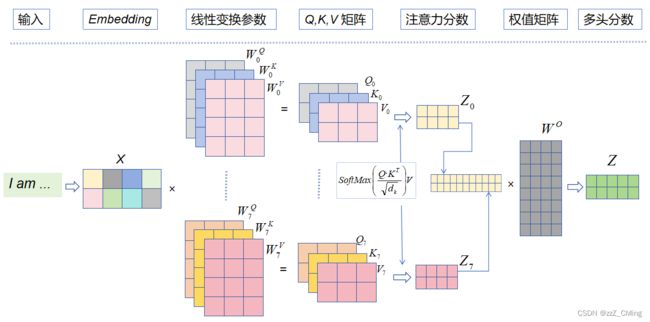
4、Multi-Head Attention 多头
在多头注意力下,每组注意力单独维护不同的Q, K, V 矩阵。
例如:8组线性变化参数 W ( Q , K , V ) W(Q,K,V) W(Q,K,V)得到8组(Q, K, V )矩阵,进而得到8组注意力 Z ( Z 0 , Z 1 , . . , Z 7 ) Z(Z_0,Z_1,..,Z_7) Z(Z0,Z1,..,Z7)。
- 将8组注意力 ( Z 0 , Z 1 , . . , Z 7 ) (Z_0,Z_1,..,Z_7) (Z0,Z1,..,Z7)拼接起来;
- 将拼接后的矩阵,与一个权值矩阵 W O W^O WO相乘;
- 得到最终的多头分数 Z Z Z,( Z Z Z中包含了所有注意力头的信息),最后输入 F N N FNN FNN中。
多头注意力层的计算公式:

多头注意力层的实质:
Multi-Head Attention实际寻找了输入序列不同角度的关联关系,经过拼接后,将不同子空间捕捉到的关联关系再综合起来,得到更高维度的连接。
5、Masked Multi-Head Attention 掩码多头
掩码多头(Masked Multi-Head Attention )只存在于Decoder过程中,
- 掩码多头的输入:标签值对应的词向量矩阵;
- 掩码多头的输出:也是注意力分数,与普通多头的区别在于会添加额外的掩码操作,使注意力只包含前序词语的影响。(掩码多头的输出,用于后续Q 矩阵的计算)
我们知道Self-Attention的计算公式为: A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q ⋅ K T d k ) V Attention(Q,K,V)=softmax(\frac{Q·K^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dkQ⋅KT)V,而掩码多头Masked Multi-Head Attention 就是在 s o f t m a x ( ) softmax() softmax()之前,添加一层Mask掩码操作。
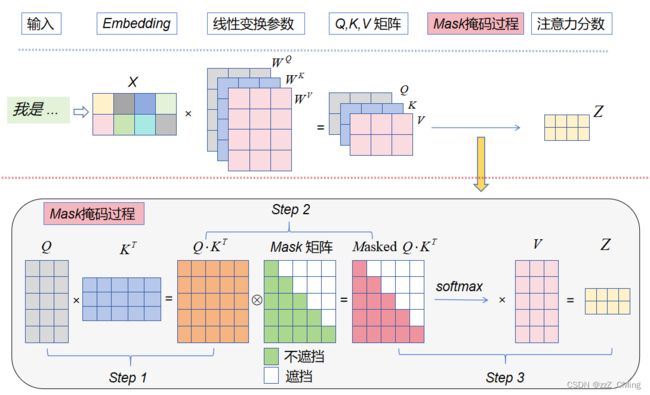
Mask掩码过程:
- Step 1:Q与K的转置做内积,得到 Q ⋅ K T Q·K^T Q⋅KT矩阵;
- Step 2: Q ⋅ K T Q·K^T Q⋅KT矩阵与Mask矩阵对位相乘,得到Masked Q ⋅ K T Q·K^T Q⋅KT矩阵;
- Masked Q ⋅ K T Q·K^T Q⋅KT矩阵经过 S o f t m a x ( ) Softmax() Softmax()操作,再与V相乘,得到掩码多头注意力输出;
Mask矩阵:按行参与计算,预测当下第 i 个词的时候,会掩盖住 i 之后所有的词,保证Mask注意力包含前序词语的影响;
6、展示
下边是两个句子中 it 与上下文单词的关系热点图。
只改变句子的最后一个单词,it 的指代就发生了转变——左图中的 it 与 animal 关系很强,右图 it 与 street 关系很强。
总结
- Self-Attention 结构,其中用到的 Q, K, V矩阵通过输入进行线性变换得到;
- Transformer 中 Multi-Head Attention 中有多个 Self-Attention,可以捕获单词之间多种维度上的相关系数(注意力分数attention score);
参考:
超详细图解Self-Attention
熬了一晚上,我从零实现了Transformer模型,把代码讲给你听
self-attention自注意力机制
致谢!