BellmanFord算法 Java实现

算法导入

上文中我们讲述了Floyd算法。什么？你还不知道啥是Floyd算法，那赶紧去瞅瞅，地址：Floyd算法 Java实现 超简单
还是那句话，栽一棵树最好的时候是十年前，其次是现在。

优点：

• 能求出每对结点之间的最短路
• 能作用于任何图，无论权值正负
• 还能检测出 负环

缺点：

• 时间复杂度为O(N^3)
• 空间复杂度为 O(N^2)

这也太高了吧。对于如今大数据中的一些图处理，N甚至会百万级别，这个时空复杂度是无法接受。难受啊，马飞！
那么，为了引出能处理大图的算法 - Johnson算法，咱们先来讲一讲前置算法，Bellman-Ford算法，因为前者是基于后者实现的。下面还是放图，让大家清楚的知道不同算法之间区间。

啥是负环

图论中，对于w(u,v) 即 点u 到 v 的权值，有三种可能，正数，负数，0。

• 正数：这个好理解，可以理解为 从u 到 v 所消耗的时间、金钱。
• 0：从 u 到 v 没有代价。
• 负数：什么情况下会出现负的权值呢？以骑士救公主为例。假设骑士初始生命值为100，骑士勇敢且机智，走到哪都要说声，“公主你在哪，俺来啦！”。牛头马面闻声赶来，一顿霍霍，骑士艰难取胜尽显颓势，生命值掉到 30啦！“前路漫漫，难道还是不行吗？” 骑士审视内心，感叹道。突然掉进一个山洞，里面摆着绝世秘籍和灵丹妙药，哈哈哈，一阵修炼后，生命值冲到10000000，武力值达到顶峰。我就问还有谁！我要救十个！

这个世界是公平的，你努力工作挣钱为正，花钱玩乐宽心为负。有舍才有得嘛！

讲到这应该不难理解了吧。

倘若图中权值存在正负值，那么存在三种可能，走过一条路回来的时候，发现钱多了、不变、少了。

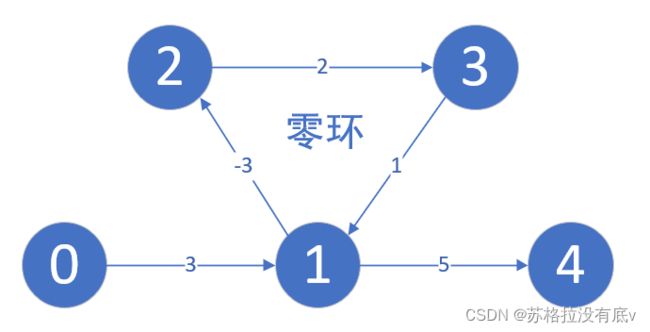
1-2-3-1，构成一个环且权值和 > 0，我们称其为正环。

构成一个环且权值和 = 0，我们称其为零环

构成一个环且权值和 < 0，我们称其为负环

一定存在最短路？

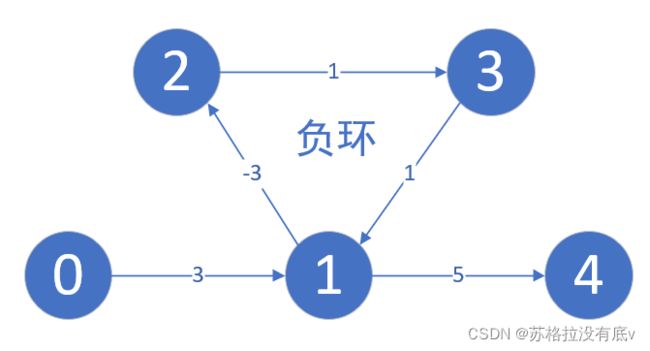
由于负环的存在，如上图中 结点 0 到 2 的最短路径，随着环的圈数越来越多，最短路径长度也越来越小，如刚开始 0 -> 1 -> 2 = 0，变成 0 -> 1 -> 2 -> 3 -> 1 -> 2 = -1，每多一圈，距离就会 减少 1。显然最短路不存在。同理，结点 0 到 其他结点 的最短路也不存在。
由此，我们可以得出一个结论。

从源点S出发，能抵达一个负环，说明该点到其他点的最短路径不存在。

算法核心

了解负环的定义以及最短路不一定存在后，我们深入算法核心，看看BellmanFord算法如何实现。

流程

定义：dis(u) ：源点 s 到 u 点的最短路长度。

松弛操作：对于边 (u,v) 松弛操作为： dis(v) = min(dis(v) , dis(u) + w(u,v) )。尝试用 S -> u -> v 的最短路径 更新 S -> v的最短路径 ，如果这条路径更优，那么就更新，这跟我们前面讲过的Dijkstra算法 操作一致。

重复：

• 每一次循环，对图中所有的边都进行一次松弛操作。
• 当一次循环中，没有成功的松弛操作，算法结束。

可以确定的是。每一次循环，我们遍历所有的边，时间复杂度为O(m)。

循环次数如何求出呢？首先可以确定的是，最短路径中，一定不存在环。

• 存在正环或零环，那么去掉正环或零环，路径还能更短，不符合
• 存在负环，那么最短路径都没有。由前面结论得出。

因此，最短路径中，n个点组成的有向图，不能存在回路，最短路径边最多有 n - 1条，即 0 -> 1 -> 2 -> ... -> n-1。

最好情况下，一次循环就全部松弛到位，那么循环次数为 1，如下图。

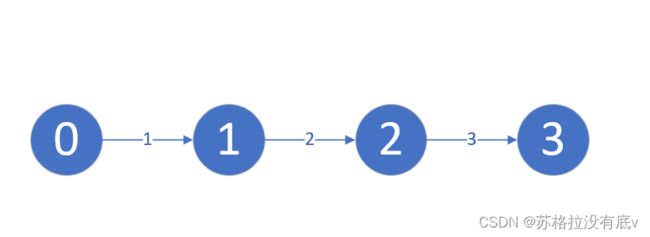
假设 源点为 0，int[][] edges = {{0, 1, 1}, {1, 2, 2}, {2, 3, 3}}，初始条件下 dis[s] = 0, dis[其他点] = 正无穷
那么第一次循环：
dis[0] = 0
dis[1] = min(dis[1], dis[0] + w[0][1]) = 1;
dis[2] = min(dis[2], dis[1] + w[1][2]) = min(正无穷, 1 + 2) = 3;
dis[3] = min(dis[3], dis[2] + w[2][3]) = min(正无穷, 3 + 3) = 6

第二次循环，发现无法松弛了，那么退出循环，循环次数为1

在最短路存在情况下，由于一次松弛操作会使最短路边数至少 + 1 不松弛边，那么就退出循环了，而最短路径边最多为 n - 1（前面证明得出）。所以最坏情况下，我们需要循环 n - 1 次，才能求出最短路径，总的时间复杂度为O(nm)。

注：本人苦思冥想后依然没有找到恰好循环 n - 1次后才求出最短路径的情况，无法放图让大家更好理解，希望读者找到后能告知。

当循环次数超过 n 次时，说明从 S 点能够走到一个负环，松弛操作永远可以进行下次。

注：以S点为源点进行BellmanFord算法，找不到负环情况下，并不能说明整个图中不存在负环。如果需要判断整个图中都不存在负环，那么需要建议一个超级源点，向图上每一个结点连一条权值为 0 的边，然后以超级源点为起点执行BellmanFord算法

代码实现

BellmanFord 算法的时间复杂度为 O(nm)，n 为图中点的个数，m为图中边点条数。

• 对于稀疏图 m ≈ n
• 对于稠密图 m ≈ n ^ 2

由于邻接矩阵在稀疏图上效率很低（尤其是在点数较多的图上，空间无法承受），所以一般只会在稠密图上使用邻接矩阵。
而邻接表存储各种图都比较合适。推荐采用邻接表方式。

import java.util.*;

/**
 * @author LKQ
 * @date 2022/4/21 20:52
 * @description 对于权值存在负数或最短路并不存在的情况，Dijkstra算法将失效，这时候需要采用Bellman-Ford算法
 * 算法核心为松弛操作：对于边 (u,v) 松弛操作为：dis(v) = min(dis(v), dis(u) + w[u][v]))，Dijkstra中同样采用
 * Bellman-Ford算法不断尝试对图上每一条边进行松弛。我们每进行一轮循环，就对图上所有的边都尝试进行一次松弛操作，当一次循环中没有成功的松弛操作时，算法停止。
 * 在最短路存在的情况下，由于一次松弛操作会使最短路的边数至少 + 1，而最短路的边数最多为 n - 1 ，因此整个算法最多执行 n - 1 轮松弛操作。
 * 如果第 n 轮循环时仍然存在能松弛的边，说明从 S 点出发，能够抵达一个负环。
 */
public class Solution {
    /**
     * 存储图
     */
    List<int[]>[] graph;
    /**
     * 存储源点到其他点的最短路
     */
    int[] dis;
    /**
     * 正无穷
     */
    int INF = Integer.MAX_VALUE / 2;

    /**
     * 求最短路并判断通过s能够到达一个负环
     * @param n n个结点，编号 0..n-1
     * @param s 源点s
     * @param edges u e[0] v e[1] w(u,v) = e[2]
     * @return 是否存在负环
     */
    public boolean bellmanFord(int n, int s, int[][] edges ) {
        // 1. 初始化邻接表
        graph = new List[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int[] e: edges) {
            graph[e[0]].add(new int[]{e[1], e[2]});
        }
        // 2. 初始化源点s 到 其他点的最短路
        dis = new int[n];
        Arrays.fill(dis, INF);
        dis[s] = 0;

        // 3. flag标志，判断一轮循环过程中是否发生松弛操作
        boolean flag = false;

        // 4. bellman-Ford
        for (int i = 0; i < n; i++) {
            flag = false;
            for (int u = 0; u < n; u++) {
                // 无穷大与常数加减仍然为无穷大
                // 因此最短路长度为 inf 的点引出的边不可能发生松弛操作
                if (dis[u] == INF) {
                    continue;
                }
                for (int[] e: graph[u]) {
                    int v = e[0], w = e[1];
                    if (dis[u] + w < dis[v]) {
                        dis[v] = dis[u] + w;
                        flag = true;
                    }
                }
            }
            // 没有可以松弛的边就停止算法
            if (!flag) {
                break;
            }
        }
        // 第 n 轮循环仍然可以松弛说明s点可以抵达一个负环
        return flag;
    }
}

参考资料

OI Wiki
图灵程序设计丛书 算法 第4版

End

更迭了朝代 当时的明月换拨人看
许嵩 《拆东墙》