DAY59 503.下一个更大元素II + 42. 接雨水
503.下一个更大元素II
题目要求:
给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
示例 1:
- 输入: [1,2,1]
- 输出: [2,-1,2]
- 解释: 第一个 1 的下一个更大的数是 2;数字 2 找不到下一个更大的数;第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
思路
可以选择扩充nums数组,或者其实也可以不扩充nums,而是在遍历的过程中模拟走了两边nums。
class Solution {
public:
vector nextGreaterElements(vector& nums) {
vector result(nums.size(), -1);
if (nums.size() == 0) return result;
stack st;
st.push(0);
for (int i = 1; i < nums.size() * 2; ++i) {
if (nums[i % nums.size()] < nums[st.top()]) st.push(i % nums.size());
else if (nums[i % nums.size()] == nums[st.top()]) st.push(i % nums.size());
else {
while (!st.empty() && nums[i % nums.size()] > nums[st.top()]) {
result[st.top()] = nums[i % nums.size()];
st.pop();
}
st.push(i % nums.size());
}
}
return result;
}
}; 42. 接雨水
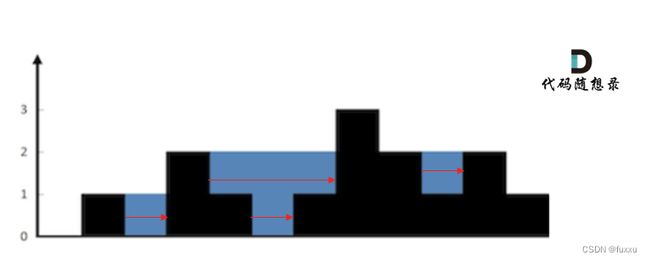
题目要求:给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
- 输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
- 输出:6
- 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
- 输入:height = [4,2,0,3,2,5]
- 输出:9
思路
本题暴力解法也是也是使用双指针。
首先要明确,要按照行来计算,还是按照列来计算。
按照行来计算如图:
按照列来计算如图:
一些同学在实现的时候,很容易一会按照行来计算一会按照列来计算,这样就会越写越乱。
我个人倾向于按照列来计算,比较容易理解,接下来看一下按照列如何计算。
首先,如果按照列来计算的话,宽度一定是1了,我们再把每一列的雨水的高度求出来就可以了。
可以看出每一列雨水的高度,取决于,该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。
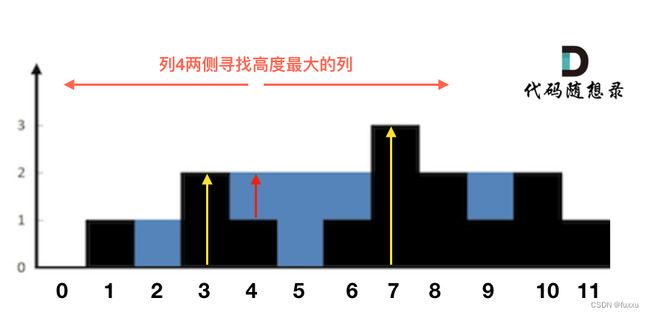
这句话可以有点绕,来举一个理解,例如求列4的雨水高度,如图:
列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
列4 右侧最高的柱子是列7,高度为3(以下用rHeight表示)。
列4 柱子的高度为1(以下用height表示)
那么列4的雨水高度为 列3和列7的高度最小值减列4高度,即: min(lHeight, rHeight) - height。
列4的雨水高度求出来了,宽度为1,相乘就是列4的雨水体积了。
此时求出了列4的雨水体积。
一样的方法,只要从头遍历一遍所有的列,然后求出每一列雨水的体积,相加之后就是总雨水的体积了。
首先从头遍历所有的列,并且要注意第一个柱子和最后一个柱子不接雨水,代码如下:
for (int i = 0; i < height.size(); i++) {
// 第一个柱子和最后一个柱子不接雨水
if (i == 0 || i == height.size() - 1) continue;
}在for循环中求左右两边最高柱子,代码如下:
int rHeight = height[i]; // 记录右边柱子的最高高度
int lHeight = height[i]; // 记录左边柱子的最高高度
for (int r = i + 1; r < height.size(); r++) {
if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i - 1; l >= 0; l--) {
if (height[l] > lHeight) lHeight = height[l];
}最后,计算该列的雨水高度,代码如下:
int h = min(lHeight, rHeight) - height[i];
if (h > 0) sum += h; // 注意只有h大于零的时候,在统计到总和中整体代码如下:
class Solution {
public:
int trap(vector& height) {
int sum = 0;
for (int i = 0; i < height.size(); i++) {
// 第一个柱子和最后一个柱子不接雨水
if (i == 0 || i == height.size() - 1) continue;
int rHeight = height[i]; // 记录右边柱子的最高高度
int lHeight = height[i]; // 记录左边柱子的最高高度
for (int r = i + 1; r < height.size(); r++) {
if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i - 1; l >= 0; l--) {
if (height[l] > lHeight) lHeight = height[l];
}
int h = min(lHeight, rHeight) - height[i];
if (h > 0) sum += h;
}
return sum;
}
}; 因为每次遍历列的时候,还要向两边寻找最高的列,所以时间复杂度为O(n^2),空间复杂度为O(1)。
力扣后面修改了后台测试数据,所以以上暴力解法超时了。
单调栈解法
单调栈就是保持栈内元素有序。通常是一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置,此时我们就要想到可以用单调栈了。
而接雨水这道题目,我们正需要寻找一个元素,右边最大元素以及左边最大元素,来计算雨水面积。
准备工作
那么本题使用单调栈有如下几个问题:
1. 首先单调栈是按照行方向来计算雨水,如图:
知道这一点,后面的就可以理解了。
2. 使用单调栈内元素的顺序
从大到小还是从小到大呢?
从栈头(元素从栈头弹出)到栈底的顺序应该是从小到大的顺序。
因为一旦发现添加的柱子高度大于栈头元素了,此时就出现凹槽了,栈头元素就是凹槽底部的柱子,栈头第二个元素就是凹槽左边的柱子,而添加的元素就是凹槽右边的柱子。
如图:
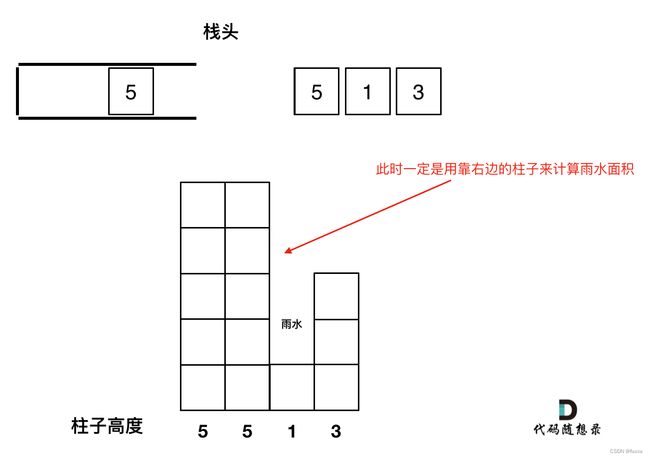
3. 遇到相同高度的柱子怎么办。
遇到相同的元素,更新栈内下标,就是将栈里元素(旧下标)弹出,将新元素(新下标)加入栈中。
例如 5 5 1 3 这种情况。如果添加第二个5的时候就应该将第一个5的下标弹出,把第二个5添加到栈中。
因为我们要求宽度的时候 如果遇到相同高度的柱子,需要使用最右边的柱子来计算宽度。
如图所示:
4. 栈里要保存什么数值
使用单调栈,也是通过 长 * 宽 来计算雨水面积的。
长就是通过柱子的高度来计算,宽是通过柱子之间的下标来计算,
那么栈里有没有必要存一个pair
其实不用,栈里就存放下标就行,想要知道对应的高度,通过height[stack.top()] 就知道弹出的下标对应的高度了。
所以栈的定义如下:
stack st; // 存着下标,计算的时候用下标对应的柱子高度 明确了如上几点,我们再来看处理逻辑。
单调栈处理逻辑
以下逻辑主要就是三种情况
- 情况一:当前遍历的元素(柱子)高度小于栈顶元素的高度 height[i] < height[st.top()]
- 情况二:当前遍历的元素(柱子)高度等于栈顶元素的高度 height[i] == height[st.top()]
- 情况三:当前遍历的元素(柱子)高度大于栈顶元素的高度 height[i] > height[st.top()]
先将下标0的柱子加入到栈中,st.push(0);。 栈中存放我们遍历过的元素,所以先将下标0加进来。
然后开始从下标1开始遍历所有的柱子,for (int i = 1; i < height.size(); i++)。
如果当前遍历的元素(柱子)高度小于栈顶元素的高度,就把这个元素加入栈中,因为栈里本来就要保持从小到大的顺序(从栈头到栈底)。
代码如下:
if (height[i] < height[st.top()]) st.push(i);如果当前遍历的元素(柱子)高度等于栈顶元素的高度,要跟更新栈顶元素,因为遇到相相同高度的柱子,需要使用最右边的柱子来计算宽度。
代码如下:
if (height[i] == height[st.top()]) { // 例如 5 5 1 7 这种情况
st.pop();
st.push(i);
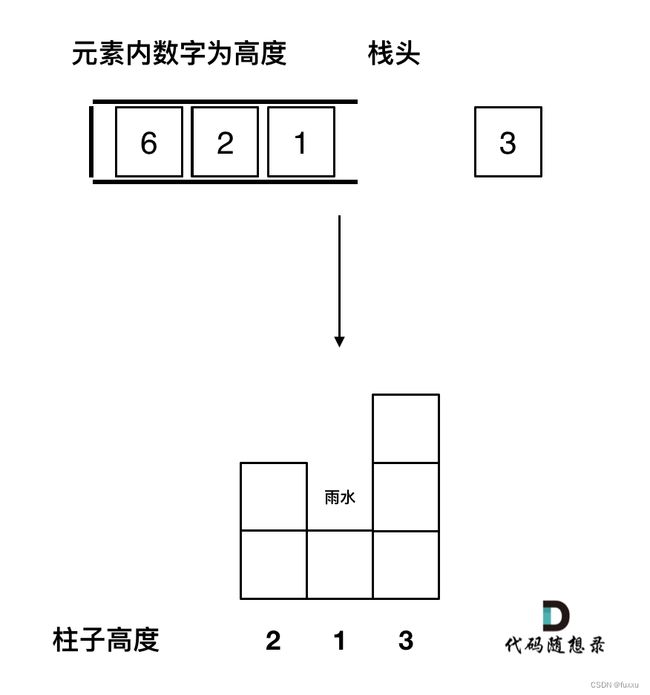
}如果当前遍历的元素(柱子)高度大于栈顶元素的高度,此时就出现凹槽了,如图所示:
取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下标记为mid,对应的高度为height[mid](就是图中的高度1)。
此时的栈顶元素st.top(),就是凹槽的左边位置,下标为st.top(),对应的高度为height[st.top()](就是图中的高度2)。
当前遍历的元素i,就是凹槽右边的位置,下标为i,对应的高度为height[i](就是图中的高度3)。
此时大家应该可以发现其实就是栈顶和栈顶的下一个元素以及要入栈的元素,三个元素来接水!
那么雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度,代码为:int h = min(height[st.top()], height[i]) - height[mid];
雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1(因为只求中间宽度),代码为:int w = i - st.top() - 1 ;
当前凹槽雨水的体积就是:h * w。
求当前凹槽雨水的体积代码如下:
while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while,持续跟新栈顶元素
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1; // 注意减一,只求中间宽度
sum += h * w;
}
}class Solution {
public:
int trap(vector& height) {
if (height.size() <= 2) return 0;
stack st;
st.push(0);
int sum = 0;
for (int i = 1; i < height.size(); ++i) {
if (height[i] < height[st.top()]) {
st.push(i);
} else if (height[i] == height[st.top()]) {
st.pop();
st.push(i);
} else {
while (!st.empty() && height[i] > height[st.top()]) {
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1;
sum += h * w;
}
}
st.push(i);
}
}
return sum;
}
};