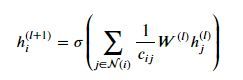GCN论文笔记
1.SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS(GCN)
解决的是图结构上的半监督分类问题，只有一部分结点有标签
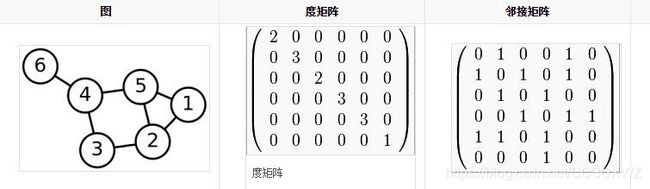
归一化后的拉普拉斯矩阵,下式中L表示拉普拉斯矩阵，D为度矩阵，A是领接矩阵：
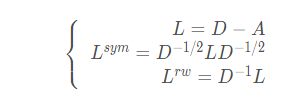
元素级别定义
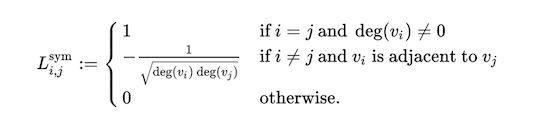
正则化的拉普拉斯矩阵，Λ是特征值对角矩阵， U为拉普拉斯矩阵L的特征值矩阵。
L = D − A L = D − 1 / 2 L D − 1 / 2 = D − 1 / 2 ( D − A ) D − 1 / 2 = D − 1 / 2 D D − 1 / 2 − D − 1 / 2 A D − 1 / 2 = I N − D − 1 / 2 A D − 1 / 2 = U Λ U T L = D-A \\ L = D^{-1/2}LD^{-1/2} = D^{-1/2}(D-A)D^{-1/2}\\=D^{-1/2}DD^{-1/2}-D^{-1/2}AD^{-1/2}\\= I_N - D^{-1/2}AD^{-1/2} = U\Lambda U^T L=D−AL=D−1/2LD−1/2=D−1/2(D−A)D−1/2=D−1/2DD−1/2−D−1/2AD−1/2=IN−D−1/2AD−1/2=UΛUT
假设：有连边 的结点可能有着相同的标签，
谱域GCN，先用U 做傅里叶变换，将x从空域转换成谱域，然后做图卷积操作，再变换回来
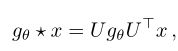
计算时间复杂度高，可由切比雪夫多项式近似
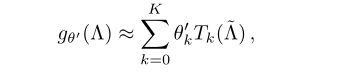
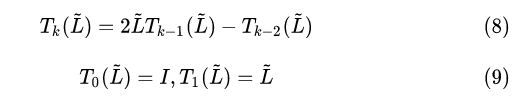
切比雪夫多项式的实现
for k in range(2, self.cheb_k):
support_set.append(torch.matmul(2 * supports, support_set[-1]) - support_set[-2])
supports = torch.stack(support_set, dim=0)
切比雪夫图卷积
x_g = torch.einsum("knm,bmc->bknc", supports, x)
x_g = x_g.permute(0, 2, 1, 3) # B, N, cheb_k, dim_in
x_gconv = torch.einsum('bnki,nkio->bno', x_g, weights) + bias #b, N, dim_out
获取对称归一化的拉普拉斯矩阵
def normalized_laplacian(w: np.ndarray) -> np.matrix:
d = np.array(w.sum(1)) #D
d_inv_sqrt = np.power(d, -0.5).flatten() #D^-1/2
d_inv_sqrt[np.isinf(d_inv_sqrt)] = 0.
print(d,d_inv_sqrt)
d_mat_inv_sqrt = np.eye(d_inv_sqrt.shape[0]) * d_inv_sqrt.shape #I_N
return np.identity(w.shape[0]) - d_mat_inv_sqrt.dot(w).dot(d_mat_inv_sqrt) #I_N - D-1/2AD-1/2
https://zhuanlan.zhihu.com/p/106687580
从谱域过度到空域，GCN所做的优化是把K阶切比雪夫降到一阶近似，每次图卷积只聚合一阶邻接结点的特征。
一阶近似是为了减少参数量，减低过拟合，空域GCN，GCN原文给的是两层的网络例子，上一层的输出是下一层的输入
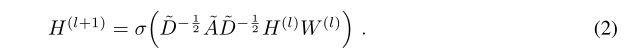
其中 A ~ \widetilde{A} A 表示带上身结点信息的邻接矩阵， I N I_N IN为单位矩阵， A A A为邻接矩阵
对 A ~ \widetilde{A} A 按行求和得到结点的度矩阵 D D D：
或者写成：
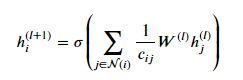
其中， N ( i ) N(i) N(i)表示结点 i i i的度
图卷积网络的公式：
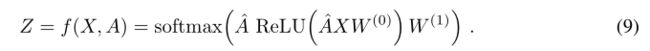
其中，邻接矩阵一般使用正则化后的拉普拉斯矩阵，
拥有范围为[ 0 , 2 ] 的特征值，这将会导致数值不稳定性和梯度爆炸/消失
GCN的局限：
-
整图训练（full-batch training），耗内存和GPU,通过mini-batch随机梯度下降可缓解，对于稠密图，需要更大的K阶近似（多跳邻居结点信息）
-
不支持边的特征，邻居关系为0或1，代表有边或无边；局限于无向图。可以将有向图转换成二分无向图，并在原始图中添加表示边的节点，可以同时处理有向边和边特征
-
假设。局部性,对于有k层的邻域依赖，自连接与相邻节点边的同等重要性。可以通过参数λ来平衡
-
网络中的每一层的邻接矩阵是共享的
-
transductive,不能处理没有见过的结点，一旦图结构发生变化，需要重新训练
-
无法处理有向图，GCN是的推导是从谱图卷积来的，要求laplace矩阵是对称的，不对称的矩阵无法进行谱分解，无法做傅里叶变换
解决图卷积层网络加深效果下降：Residual Connection
每增加一层，有效上下文大小为顶点增加一个十阶邻域(对于有k层的模型)。此外，随着模型深度的增加，过度拟合可能导致参数数量增加
2.Graph Attention network(GAT)
解决的是无法区分邻接结点区分度的问题，隐式邻居结点指定不同的权重，最初提出用于解决节点分类任务
基本过程：
（1）计算注意力系数 e i e_i ei,结点特征相似度 e i , j e_{i,j} ei,j是一个常数
输入结点特征 h ∈ R N × F h∈R^{N×F} h∈RN×F, N N N为结点个数， F F F为结点特征维度
计算结点 i i i 与结点 j j j 的注意力分数
其中， h i h_i hi, h j h_j hj是一维向量，W是权重
a是一个共享的attention机制, a:R(F’)->R(F’),用来计算注意力系数，是一个可学习的参数
-
点乘
-
余弦相似度
-
标度点积 softmax(QK/√d) V
（2） 计算每个邻居结点的重要程度，即weight， α i , j ∈ [ 0 , 1 ] α_{i,j }\in[0,1] αi,j∈[0,1]，用softmax进行归一化
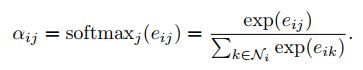
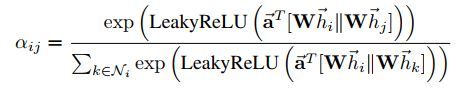
(3) 对邻居结点特征进行加权求和，σ用于增加非线性
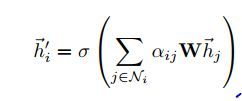
下面是一个结点特征的具体计算实例
（4）多头注意力：
非最后一层，拼接 h’∈R(K×F)
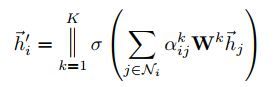
最后一层，则 K 个 Attention 的输出不进行拼接，求平均 h ′ ∈ R F h'\in R^F h′∈RF。连接就不再合理，取而代之的是采用平均法,保持维度一致，每个 h ′ ∈ R F h'\in R^F h′∈RF，而不是 h ′ ∈ R K × F h'\in R^{K×F} h′∈RK×F
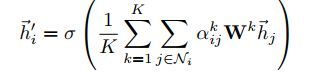
最后输出的结点特征：
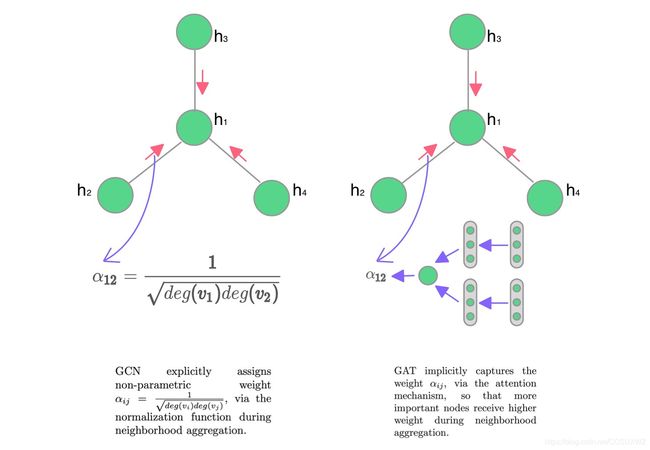
GAT的图示表示：
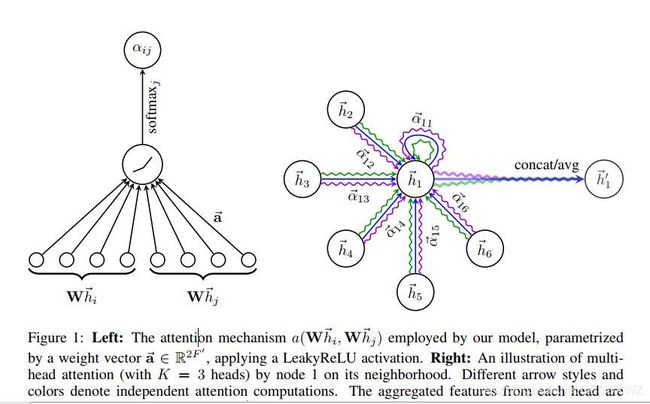
可以发现，GAT的计算全程没有邻接矩阵的参与。计算时间复杂度O(|V|FF’+|E|F’)，其中，|V|FF’是结点特征变换Wh,|E|F’为计算注意力系数
GAT 不依赖于完整的图结构（A），只依赖于边E。因此可以用于 inductive 任务。
性质：
（1）操作效率高，可以并行计算
（2）通过对邻域指定任意的权值，它可以应用于不同度的图节点
(3) 可用于inductive的任务，可以泛化到没有见过的结点
（4）适用有向图，逐顶点计算的方式，摆脱了拉普拉斯的限制
比较：
（1）GCN与GAT都是将邻居顶点的特征聚合到中心顶点上，利用图的局部不变性学习新的结点表达，不同的是GCN利用了拉普拉斯矩阵，GAT利用attention系数。
GCN：
GAT:
GAT局限
（1）没有充分使用边的特征：GAT没有充分利用边的信息，只利用到了连接性，即在邻接矩阵中值为1表示有连接，值为0，表示不相连。然而，图中的边通常具有很多信息，例如强度、类型等。并且不仅仅是二进制的变量，可能是连续的、多维的。GCN能够利用一维的边的特征，也就是边的权重，但是仅限于使用一维的边的特征。
（2）原始邻居矩阵可能存在噪声：每个GAT或GCN层根据作为输入的原始邻接矩阵过滤节点特征。原始邻接矩阵可能存在噪声且不是最优的，这将限制滤波操作的有效性。
3.Inductive Representation Learning on Large Graphs (GraphSAGE)
以往工作是整图训练的，需要所有结点的参与（transductive）,不能处理unseen node, 本文提出了一种inductive的方法，GraphSage , 学习一个函数，对局部的邻居结点进行采样，并聚合邻居结点的特征，在inference阶段，可以生成unseen nodes的embedding表示
到目前为止，图卷积网络(GCNs)只应用于具有固定图的transductive设置，已有的GCNs不适应于大图，被设计用来做整图分类。
Inductive learning的挑战：识别节点邻域的结构属性，这些属性既显示节点在图中的局部角色，也显示其全局位置,
GraphSAGE主要分为两个过程：sample和aggregate, 通过在学习算法中加入节点特征，同时学习每个节点邻居的拓扑结构，GraphSAGE可以学习图上的结构信息
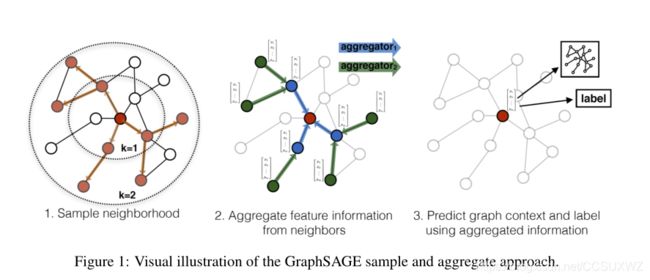
GCN需要一个完整的图结构，full graph Laplacian;
本文的核心思想是，如何聚合局部邻居结点的特征，
解释：输入，图结点集V，权重矩阵W，边集E
第1行，用结点v特征初始化hv,0, 第2行for迭代k次，第3行，对于每一个邻居结点，第4行，聚合上一次迭代的邻居结点特征，第5行，拼接上一次结点v的表示hv,k-1和邻居结点特征，并进行MLP变换，第7行，对结点v的特征做归一化，第9行，输出结点v的表示；
注意：采样的是固定大小(fixed size)的邻居列表
对称性：每个聚合函数是可微分的，可以适应于不同的输入排列，同时可以训练并保持高效的表示能力，
文章探索了三种不同的聚合器：
（1）Mean aggregator
类似于GCN，利用所有邻居结点，结点v的特征做平均
其中， h v k h_v^k hvk是更新后的结点v向量表示， h u k − 1 h_u^{k-1} huk−1是邻居结点的特征表示，U表示向量拼接
(2) LSTM aggregator
LSTMs的优点是表达能力更强，但是对于输入来说，它是非对称的，它们不是排列不变的。通过简单地对节点的邻居进行随机排列，来调整节点排序模型，使其在无序的集合上运行
(3) Pooling aggregator
Pooling 方式是可训练和对称的
