算法笔记-第九章-平衡二叉树

平衡二叉树

定义

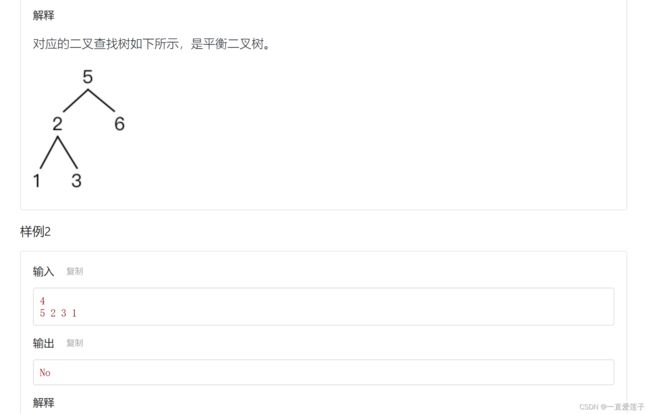
• 树还是一个二叉查找树
• 其左右树的高度之差的绝对值不超过1
  左右高度之差称为该结点的平衡因子

大佬讲解

平衡二叉树的查找操作

本质上是和查找二叉树中的查找操作是一样的

void search(node* root, int x)
{
    if (root == NULL)
    {
        printf("search failed\n");
        return;  
    }
    if (x == root->data) {                
        printf("%d\n", root->data);                   
    }
    else if (x < root->data)//如果x笔根节点的数据域小，说明x在左子树                    
    {
        search(root->lchild, x);                    
    }
    else                    
    {
        search(root->data, x);                    
    }
}

插入操作

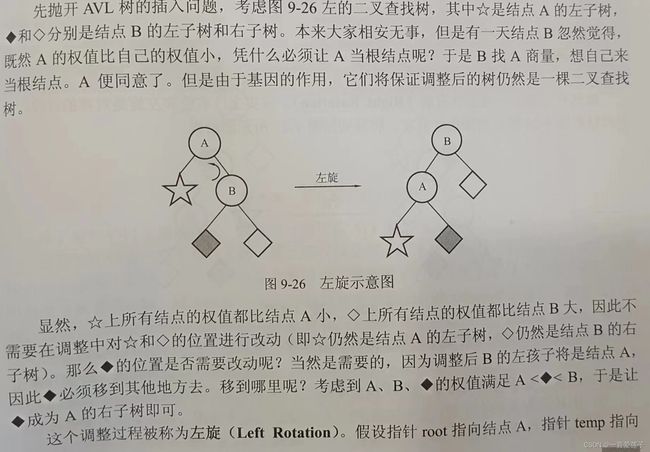
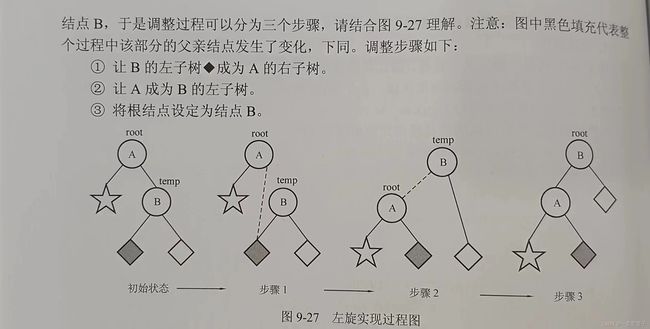
左旋操作

算法笔记-322页

void L(node* root)     
{
    node* temp = root->rchild;     
    root->rchild = temp->lchild;     
    temp->rchild = root;     

    //更新结点A的高度     
    updateHeight(root);     
    updateHeight(temp);     
    root = temp;     
}

插入情况

AVL数的插入代码是在二叉查找树的插入代码上增加平衡操作的

插入操作代码

不考虑平衡操作

void insert(node*& root, itn v)
{
    if (root == NULL)
    {
        root = newnode(v);  
        return;  
    }
    if (v < root->v)  
    {
        insert(root->lchild, v);//向左子树插入    
    }
    else     
    {
        insert(root->rchild, v);//向右子树插入     
    }
}

平衡插入操作

在这个基础上，由于需要从插入的节点开始从下往上判断结点是否失衡，因此需要在每一个insert函数之后更新当前子树的高度，并且在这之后判断树型是LL,LR,RR,RL型之一
插入权值为v的结点

void insert(node* root, int v)
{
    if (root == NULL)
    {
        root = newnode(v);
        return;
    }
    if (v < root->v)//v笔根节点的权值小
    {
        i = insert(root->lchild, v);//向左子树插入
        updateHeight(root);
        //更新树的高度

        if (getBalancefactor(root) == 2)
        {
            if (getBalancefactor(root->lchild) == 1) {//LL型
                R(root);
            }
            else if (fteBalancefactor(root->lchild == -1))
            {
                //LR型
                L(root->lchild);
                R(root);
            }
        }

    }
    else {
        insert(root->rchild, v);//向右子树插入
        updateHeight(root);//更新树高度
        if (getBalancefactor(root) == 2)
        {
            if (gteBalancefactor(root->rchild) == -2) {
                if (getBalancefactor(root->rchild) == -1) {
                    //RR型  
                    L(root);  
                }
                else if (getBalancefactor(root->rchild) == -1)//RL型  
                {
                    R(root->rchild);  
                    L(root);  
                }
            }
        }
    }
   
}

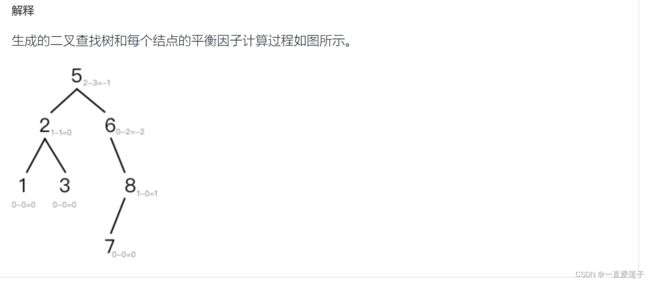
二叉查找树的平衡因子

#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;

const int MAXN = 50;

struct Node {
    int data;
    int height;
    int l, r;
} nodes[MAXN];

int nodeCount = 0;

int newNode(int data) {
    nodes[nodeCount].data = data;
    nodes[nodeCount].height = 1;
    nodes[nodeCount].l = nodes[nodeCount].r = -1;
    return nodeCount++;
}

int getHeight(int root) {
    if (root == -1) {
        return 0;
    } else {
        return nodes[root].height;
    }
}

void updateHeight(int root) {
    nodes[root].height = max(getHeight(nodes[root].l), getHeight(nodes[root].r)) + 1;
}

int getBalanceFactor(int root) {
    return getHeight(nodes[root].l) - getHeight(nodes[root].r);
}

int insert(int root, int data) {
    if (root == -1) {
        return newNode(data);
    }
    if (data < nodes[root].data) {
        nodes[root].l = insert(nodes[root].l, data);
    } else {
        nodes[root].r = insert(nodes[root].r, data);
    }
    updateHeight(root);
    return root;
}

vector<int> balanceFactor;

void inOrder(int root) {
    if (root == -1) {
        return;
    }
    inOrder(nodes[root].l);
    balanceFactor.push_back(getBalanceFactor(root));
    inOrder(nodes[root].r);
}

int main() { 
    int n, data, root = -1;  
    scanf("%d", &n);  
    for (int i = 0; i < n; i++) {  
        scanf("%d", &data);  
        root = insert(root, data);  
    }
    inOrder(root);  
    for (int i = 0; i < (int)balanceFactor.size(); i++) {  
        printf("%d", balanceFactor[i]);  
        if (i < (int)balanceFactor.size() - 1) {  
            printf(" ");  
        }
    }
    return 0;  
}

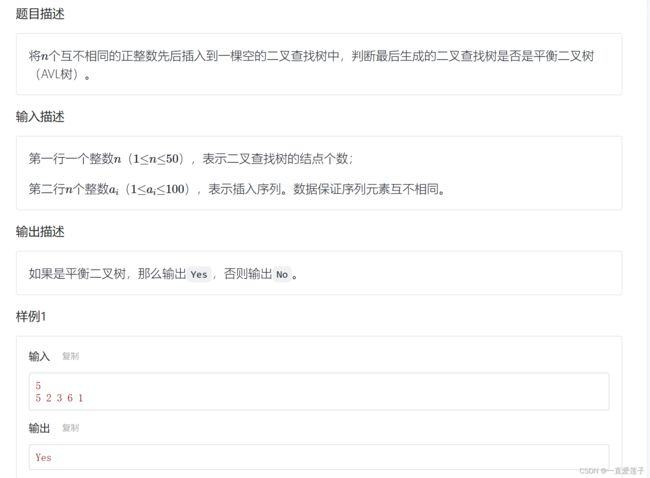
平衡二叉树的判定

#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;

const int MAXN = 50;

struct Node {
    int data;
    int height;
    int l, r;
} nodes[MAXN];

int nodeCount = 0;

int newNode(int data) {
    nodes[nodeCount].data = data;
    nodes[nodeCount].height = 1;
    nodes[nodeCount].l = nodes[nodeCount].r = -1;
    return nodeCount++;
}

int getHeight(int root) {
    if (root == -1) {
        return 0;
    } else {
        return nodes[root].height;
    }
}

void updateHeight(int root) {
    nodes[root].height = max(getHeight(nodes[root].l), getHeight(nodes[root].r)) + 1;
}

int getBalanceFactor(int root) {
    return getHeight(nodes[root].l) - getHeight(nodes[root].r);
}

int insert(int root, int data) {
    if (root == -1) {
        return newNode(data);
    }
    if (data < nodes[root].data) {
        nodes[root].l = insert(nodes[root].l, data);
    } else {
        nodes[root].r = insert(nodes[root].r, data);
    }
    updateHeight(root);
    return root;
}

bool isAVL(int root) {
    if (root == -1) {
        return true;
    }
    return isAVL(nodes[root].l) && isAVL(nodes[root].r) && abs(getBalanceFactor(root)) <= 1;

}

int main() {  
    int n, data, root = -1;  
    scanf("%d", &n);  
    for (int i = 0; i < n; i++) {  
        scanf("%d", &data);  
        root = insert(root, data);  
    }
    printf(isAVL(root) ? "Yes" : "No");  
    return 0;  
}

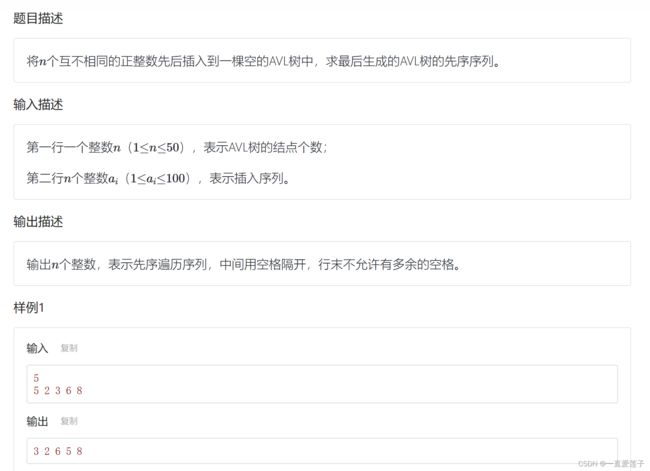
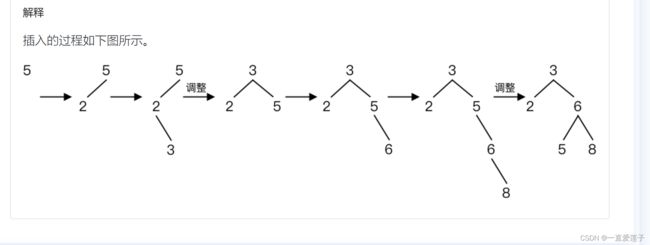
平衡二叉树的建立

#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;

const int MAXN = 50;

struct Node {
    int data;
    int height;
    int l, r;
} nodes[MAXN];

int nodeCount = 0;

int newNode(int data) {
    nodes[nodeCount].data = data;
    nodes[nodeCount].height = 1;
    nodes[nodeCount].l = nodes[nodeCount].r = -1;
    return nodeCount++;
}

int getHeight(int root) {
    if (root == -1) {
        return 0;
    } else {
        return nodes[root].height;
    }
}

void updateHeight(int root) {
    nodes[root].height = max(getHeight(nodes[root].l), getHeight(nodes[root].r)) + 1;
}

int getBalanceFactor(int root) {
    return getHeight(nodes[root].l) - getHeight(nodes[root].r);
}

int L(int root) {
    int temp = nodes[root].r;
    nodes[root].r = nodes[temp].l;
    nodes[temp].l = root;
    updateHeight(root);
    updateHeight(temp);
    return temp;
}

int R(int root) {
    int temp = nodes[root].l;
    nodes[root].l = nodes[temp].r;
    nodes[temp].r = root;
    updateHeight(root);
    updateHeight(temp);
    return temp;
}

int insert(int root, int data) {
    if (root == -1) {
        return newNode(data);
    }
    if (data < nodes[root].data) {
        nodes[root].l = insert(nodes[root].l, data);
        updateHeight(root);
        if (getBalanceFactor(root) == 2) {
            if (getBalanceFactor(nodes[root].l) == 1) {
                root = R(root);
            } else if (getBalanceFactor(nodes[root].l) == -1) {
                nodes[root].l = L(nodes[root].l);
                root = R(root);
            }
        }
    } else {
        nodes[root].r = insert(nodes[root].r, data);
        updateHeight(root);
        if (getBalanceFactor(root) == -2) {
            if (getBalanceFactor(nodes[root].r) == -1) {
                root = L(root);
            } else if (getBalanceFactor(nodes[root].r) == 1) {
                nodes[root].r = R(nodes[root].r);
                root = L(root);
            }
        }
    }
    return root;
}

vector<int> pre;

void preOrder(int root) {
    if (root == -1) {
        return;
    }
    pre.push_back(nodes[root].data);
    preOrder(nodes[root].l);
    preOrder(nodes[root].r);
}

int main() {
    int n, data, root = -1;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%d", &data);
        root = insert(root, data);
    }
    preOrder(root);
    for (int i = 0; i < (int)pre.size(); i++) {
        printf("%d", pre[i]);
        if (i < (int)pre.size() - 1) {
            printf(" ");
        }
    }
    return 0;
}