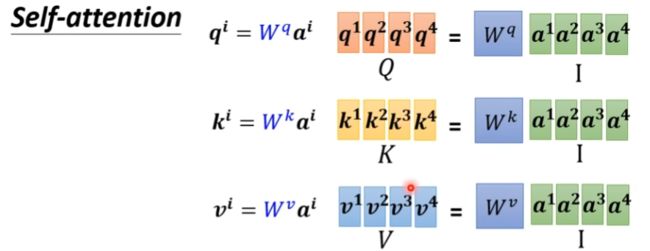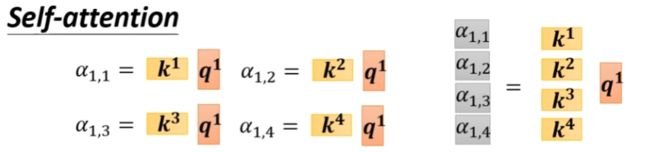机器学习笔记
目录
- 机器学习基本概念介绍
- 深度学习
- 反向传播
-
- 前向传播
- 反向传播
- pytorch
- 梯度下降算法
- 卷积神经网络(CNN)
-
- 卷积层
- 池化层
- 自注意力机制(self-attention)
- 循环神经网络(RNN)
-
- 长短期记忆递归神经网络(LSTM)
- Transformer
- 自监督学习(Self-Supervised Learning)
- BERT
-
- 预训练(Pre-train)
- 微调(Fine-tune)
机器学习基本概念介绍
机器学习 ≈ 机器自动寻找一个函数f
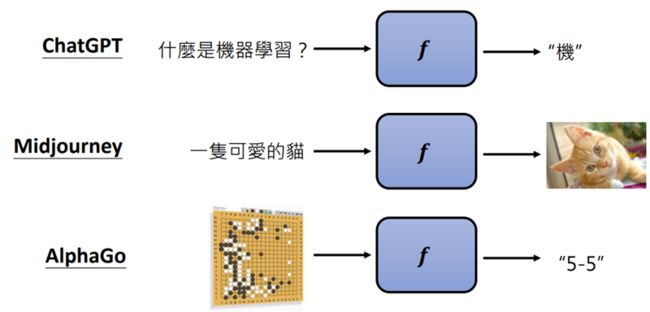
根据函数的输出可以分为两类:Regression(回归)与Classification(分类)
- Regression:函数的输出是一个数值 例如:输入输入今天的PM2.5值、温度、臭氧量等,输出明天的PM2.5值
- Classification:函数的输出是一个类别(选择题) 例如:判断一封邮件是否为垃圾邮件
机器学习不断发展不再局限于上述分类,而是变为了更加复杂的Structured Learning
- Structured Learning:结构化学习,又称为Generative Learning生成式学习,生成有结构的物件(如影像、文句等)
寻找函数的三步骤
线性模型无法准确地预测数据,我们需要得到更加复杂的模型
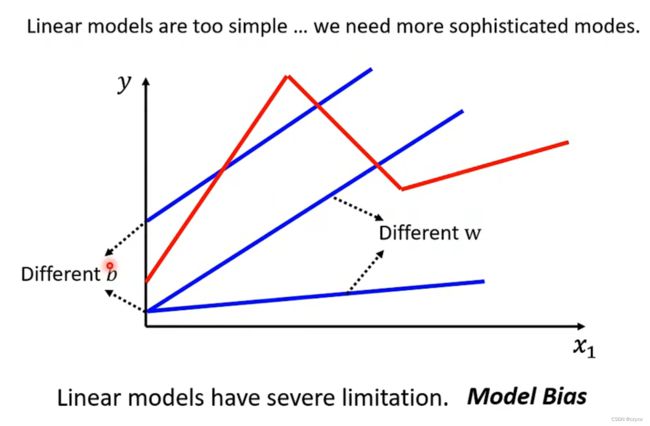
我们可以利用sigmoid function函数去模拟真实的function
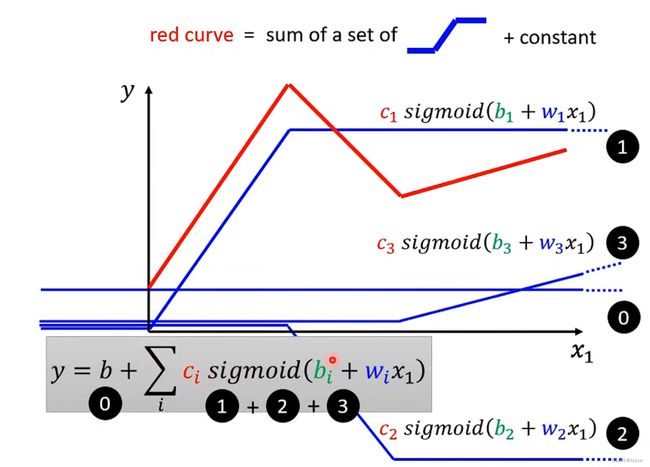


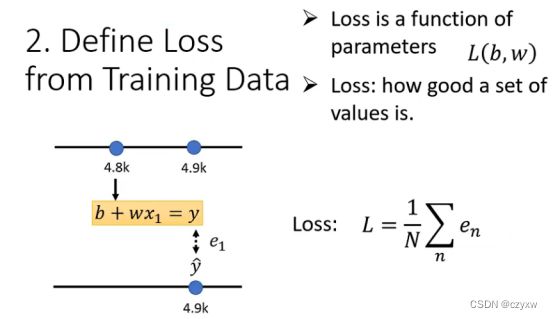
找到带未知参数的function后,通过训练数据来计算loss值,计算方法如下:

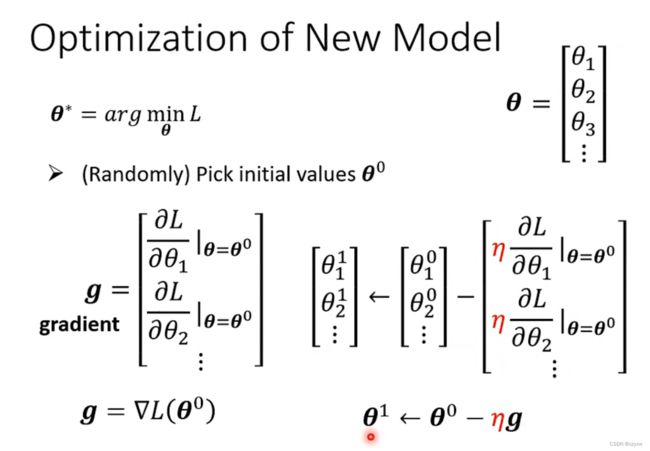
接下来进行最佳化处理,方法如下:
深度学习
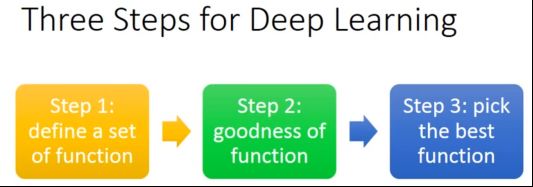
深度学习任务可以分为以下三步:
- 选定函数集合
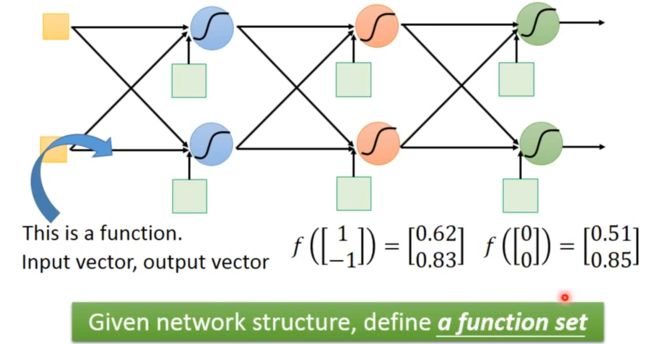
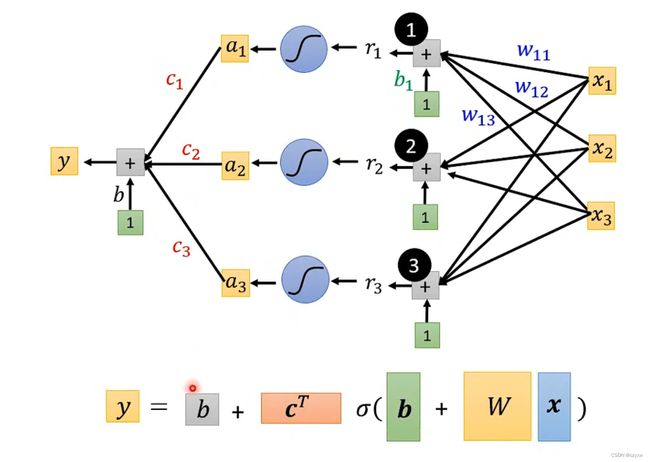
在每个神经元中都有其对应的weight和bias,神经元与神经元之间有不同的连接方式(连接方式由你自己设计),各神经元间的连接方式决定神经网络的结构。
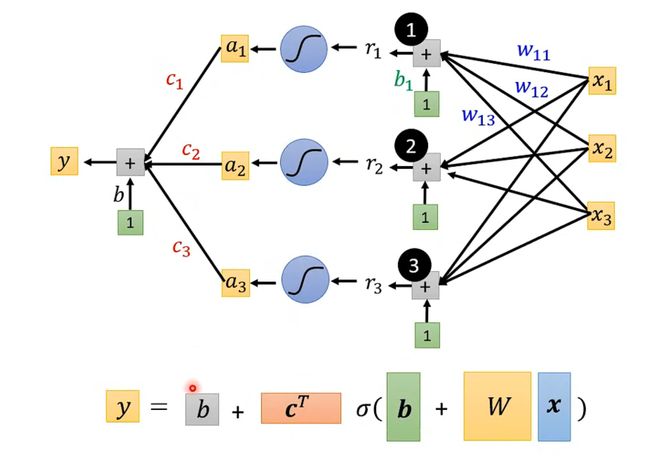
在下图中,通过已给出的输入数据和各神经元的weight和bias,利用sigmoid函数计算出最后的结果。
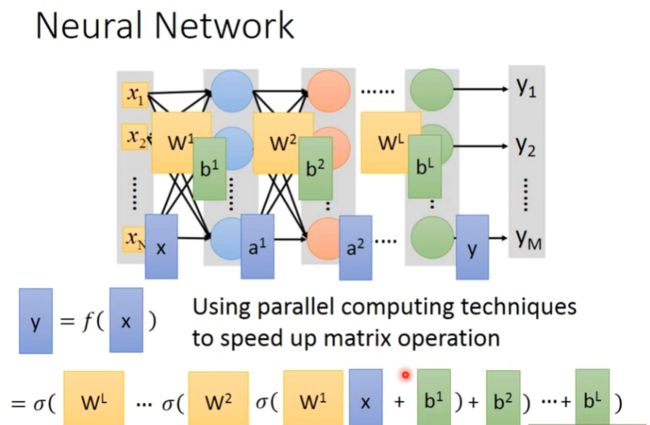
其实找到function也就是找到一个Neural Network 神经网络例图如下:矩阵计算
计算方式如下:
(1)输入第i-1层的向量
(2)利用第i层中各神经元的weight和bias以及sigmoid函数得到输出的结果,然后将第i层计算的数据给到第i+1层
(3)重复上面两步,直到输出最终的结果
- 制定评价函数优劣的标准
选定计算loss值的方法(loss值越小越好)
- 找出最好的函数
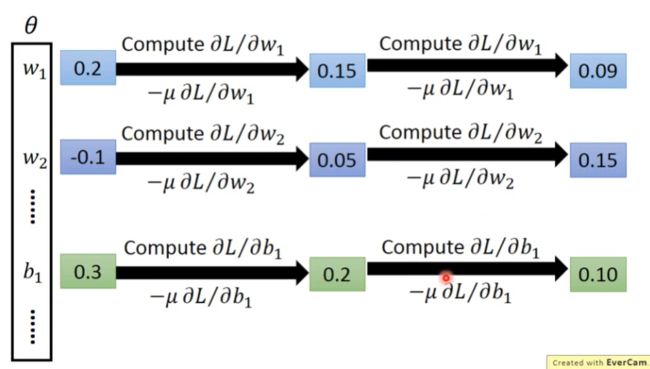
利用梯度下降算法找出最佳函数
反向传播
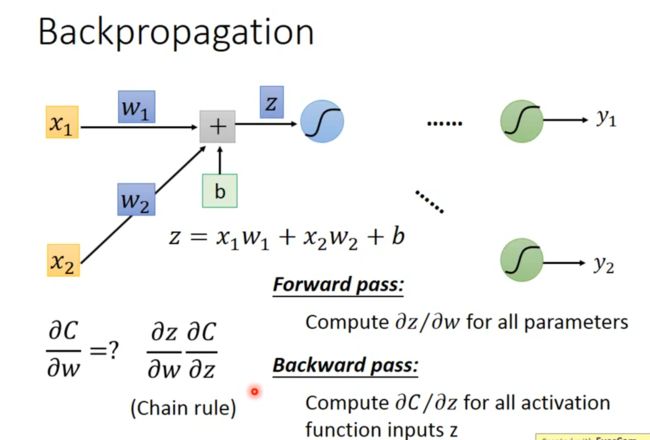
神经网络的训练过程中,前向传播和反向传播交替进行,前向传播通过训练数据和权重参数计算输出结果;反向传播通过导数链式法则计算损失函数对各参数的梯度,并根据梯度进行参数的更新
前向传播
我们拿一个神经元来举例,如下图z对w的导数值就是上一层的输入值
反向传播
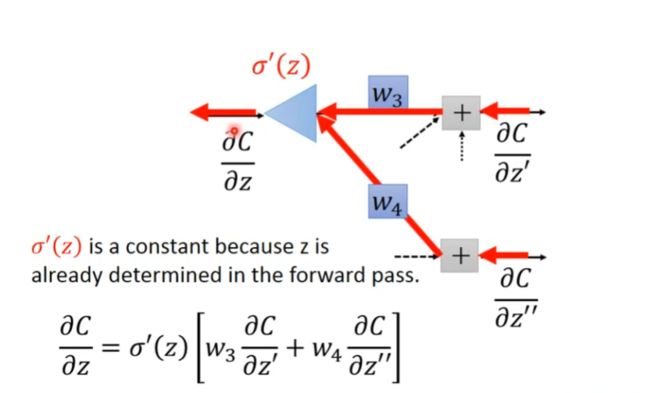
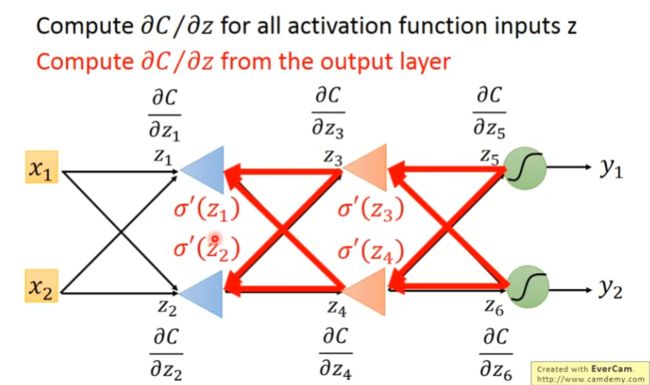
如下图,a对z的偏导由你定义的激活函数决定,而c对a的偏导与下一层的参数z’和z’'有关
c对z的偏导值如下图(c对z’和z’'的偏导值未知):
如下图所示,可以最后一层计算出c对z5和z6的偏微分,而z5和z6由决定了c对z3和z4的偏微分,即后一层可以得出前一层的微分值
pytorch
Pytorch 是一个基于 Python 的科学计算库,它面向以下两种人群:
- 希望将其代替 Numpy 来利用 GPUs 的威力;
- 一个可以提供更加灵活和快速的深度学习研究平台。
安装教程参考:pytorch安装教程
Anaconda Prompt使用的命令参考:Anaconda命令
Pytorch 安装验证是否成功:
import torch
print(torch.cuda.is_available())
进入anaconda虚拟环境中,使用上述命令,显示为True则安装成功。
若出现使用官网下的命令安装GPU版pytorch,结果却是cpu版本,可参考下文:
conda安装GPU版pytorch,结果却是cpu版本
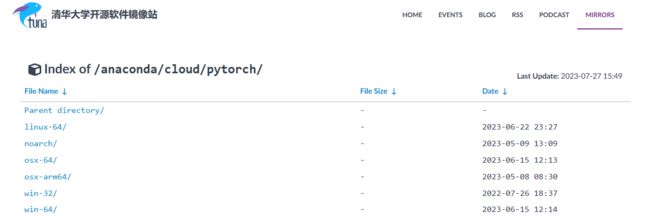
上面参考文章使用的是Linux系统,可以进入清华大学开源镜像站(如下图所示)根据你自己的系统自行选择:
pytorch、CUDA和cudatoolkit对应的版本号可以前往pytorch官网(如下图所示)查看
Pytorch 学习推荐:
pytorch快速入门
pytorch学习刘二大人
pytorch学习小土堆
梯度下降算法
参考文章:梯度下降算法原理讲解
卷积神经网络(CNN)
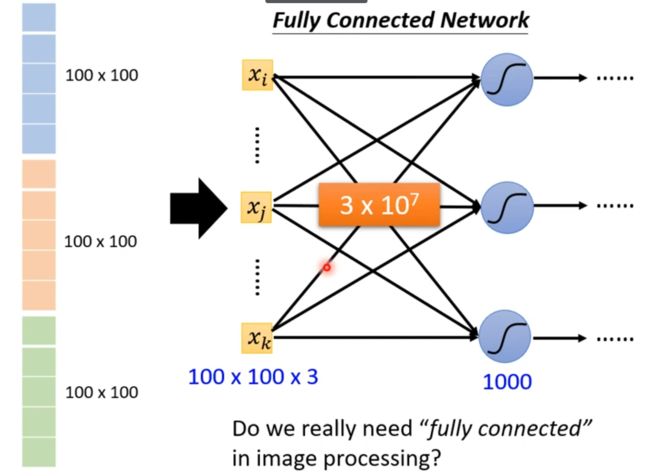
如果用全连接神经网络处理大尺寸图像具有三个明显的缺点:
(1)首先将图像展开为向量会丢失空间信息;
(2)其次参数过多效率低下,训练困难;
(3)同时大量的参数也很快会导致网络过拟合。
使用卷积神经网络可以很好地解决上面的三个问题。
卷积神经网络主要由这几类层构成:输入层、卷积层,ReLU层、池化(Pooling)层和全连接层(全连接层和常规神经网络中的一样)。通过将这些层叠加起来,就可以构建一个完整的卷积神经网络。
卷积层
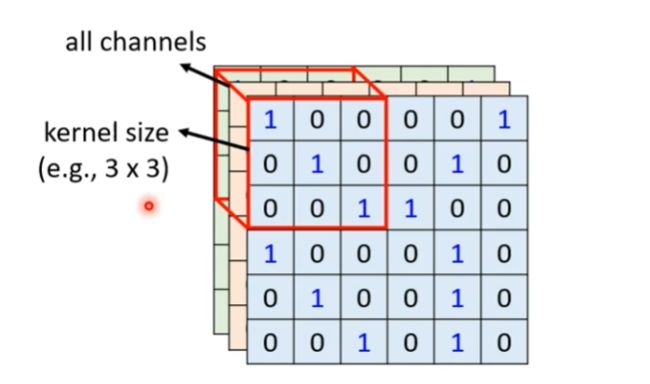
1、感受野(Receptive field)
如下图所示,红色方框中的部分叫做神经元的感受野(receptive field),它的尺寸是一个超参数。在深度方向上,这个连接的大小总是和输入量的深度相等。
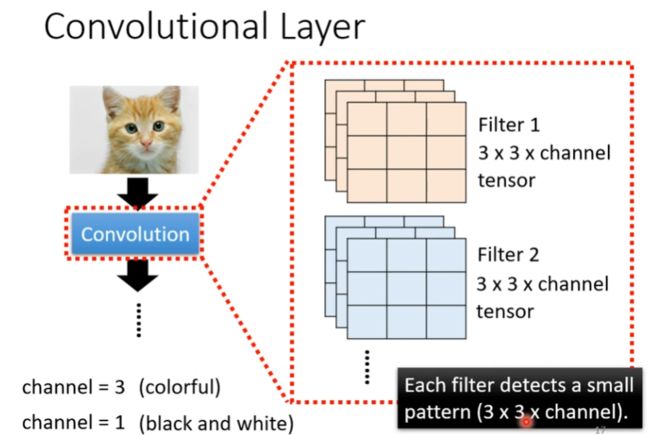
2、滤波器(Filter)
每个滤波器在空间上(宽度和高度)都比较小,但是深度和输入数据一致,网络会让滤波器学习到当它看到某些类型的视觉特征时就激活,具体的视觉特征可能是某些方位上的边界,或者在第一层上某些颜色的斑点,甚至可以是网络更高层上的蜂巢状或者车轮状图案。
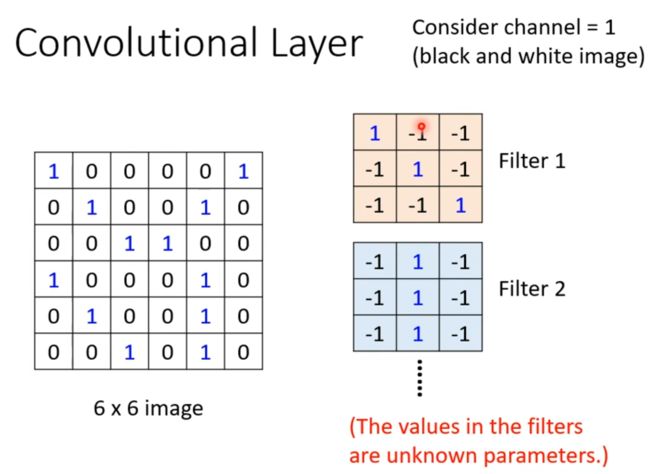
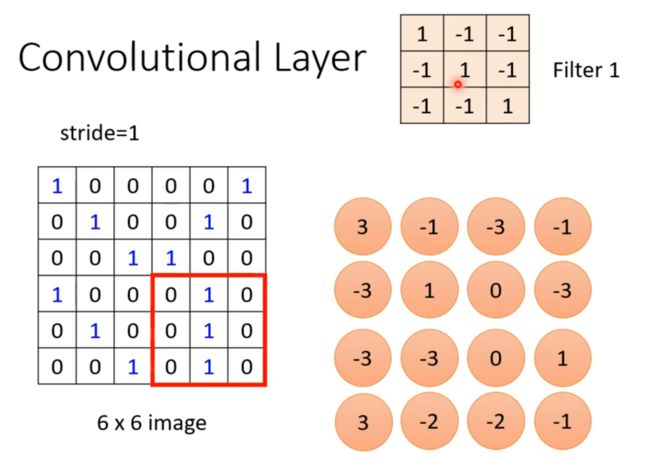
以下图为例,输入为一个6x6的黑白图片(channel=1),给出两个已知参数的filter,按以下步骤进行特征提取:
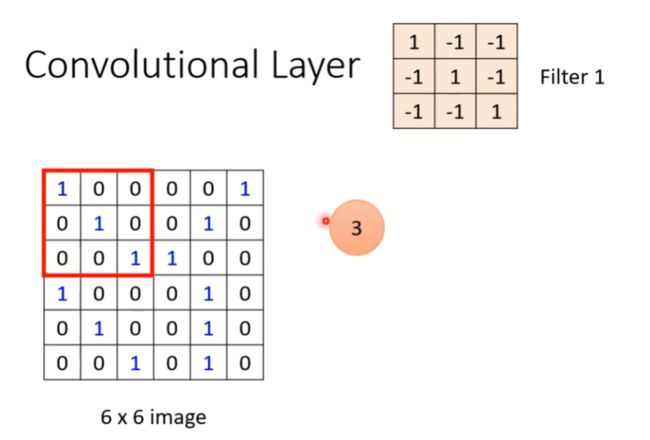
(1)将filter1放在图片的左上角,将filter1上的值与图片上的相对应的值进行相乘,将得到的结果求和得到最终值为3。
(2)定义步长(stride)为1,将filter1移动一个步长,然后重复(1)操作,得到最终值为-1。
(3)按照定义的步长,将filter1向左移动然后向下移动扫描整张图片,一直重复(1)操作,得到所有的结果,如下图所示。
以下图为例,filter1中对角线上的值均为1,即当图片中对角线上的值也均为1时(计算结果为3),可以找到所需特征在图片的具体位置。
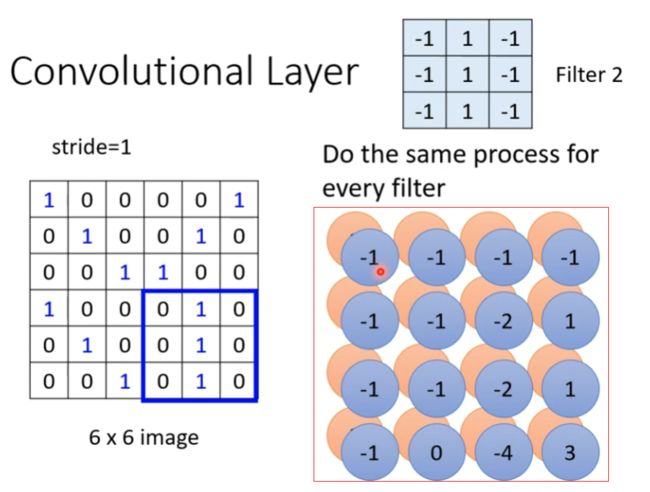
按照上述步骤,使用两个filter计算会产生两个特征图(feature map),如下图红框中所示。
以下图为例,在某次卷积中使用了64个filter就会产生64个特征图(feature map)。当把这64个特征图(feature map)当作输入再次进行卷积时,需要3x3x64的卷积层(channels=64)。
池化层
通常在连续的卷积层之间会周期性地插入一个池化层。它的作用是逐渐降低数据体的空间尺寸,这样的话就能减少网络中参数的数量,使得计算资源耗费变少,也能有效控制过拟合。
最大池化
以filter1、filter2计算出的结果为例(如下图所示),将计算结果以2x2为一组分类
在每组数据中选出一个最大值(如下图所示)
参考文章:卷积神经网络(CNN)详解
自注意力机制(self-attention)
attention机制的具体计算过程,如果对目前大多数方法进行抽象的话,可以将其归纳为两个过程:第一个过程是根据Query和Key计算权重系数,第二个过程根据权重系数对Value进行加权求和。
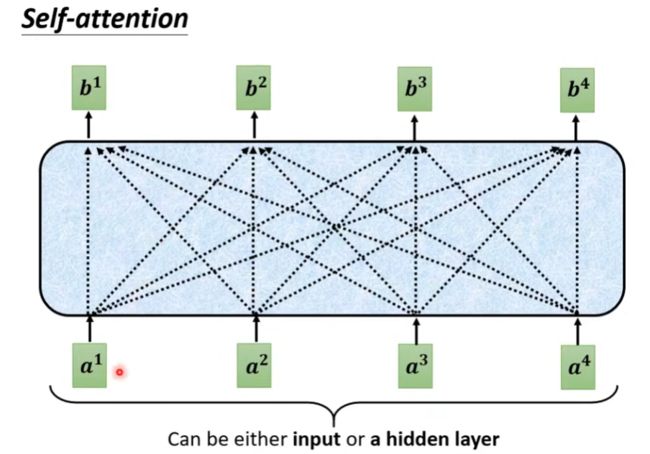
以下图a1为例来说明计算过程
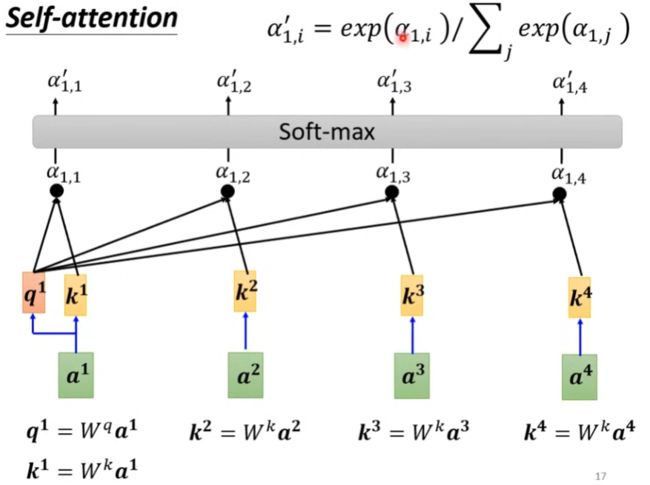
(1)计算a1与自身和其他向量a2,a3,a4的相关性
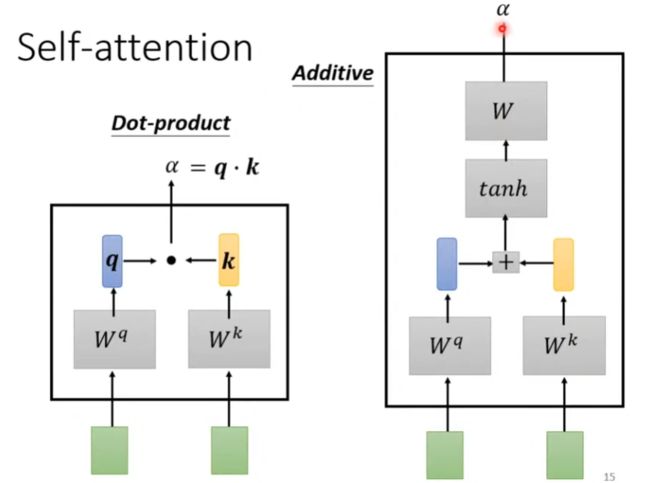
有以下两种方法(如下图),我们使用Dot-product方法
利用向量q、k通过Dot-product方法进行矩阵运算得到注意力分数,然后经过softmax计算后得到注意力权重。
(2)根据权重系数进行加权求和
其他向量a2,a3,a4也是通过上述操作来进行计算
其实向量a1,a2,a3,a4是可以同时进行计算的
将这些向量组视为矩阵,利用矩阵的运算规则来计算
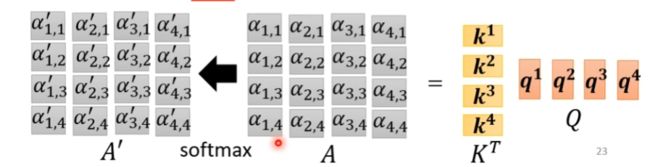
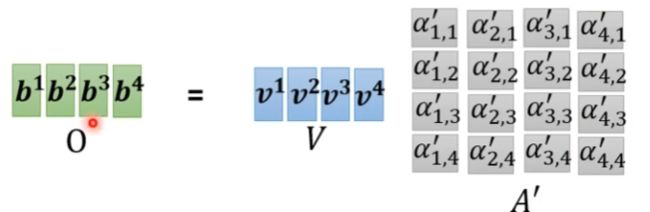
将向量组ki转置将其视为一个矩阵与q1相乘,即可得到向量a1的注意力分数
向量组ki与向量组qi视为矩阵,进行运算即可得到所有所需向量的注意力分数,进行softmax计算后得到注意力权重
向量组vi视为矩阵,与矩阵A’进行运算后得到结果。
参考文章:Attention注意力机制与self-attention自注意力机制
循环神经网络(RNN)
参考文章:循环神经网络(RNN)基础
长短期记忆递归神经网络(LSTM)
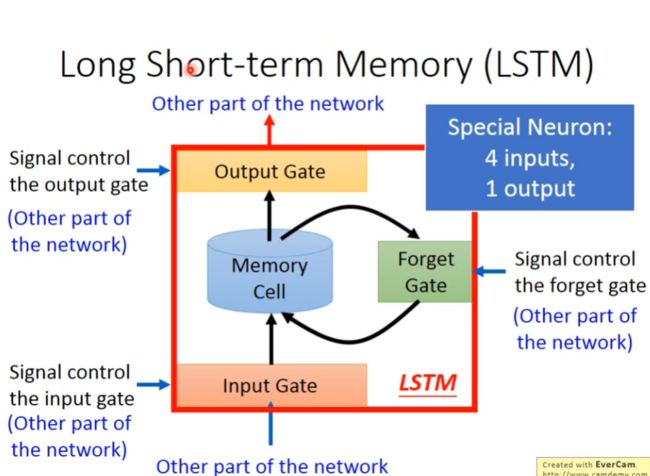
与一般神经网络不同的是,LSTM有四个输入,其结构图如下:
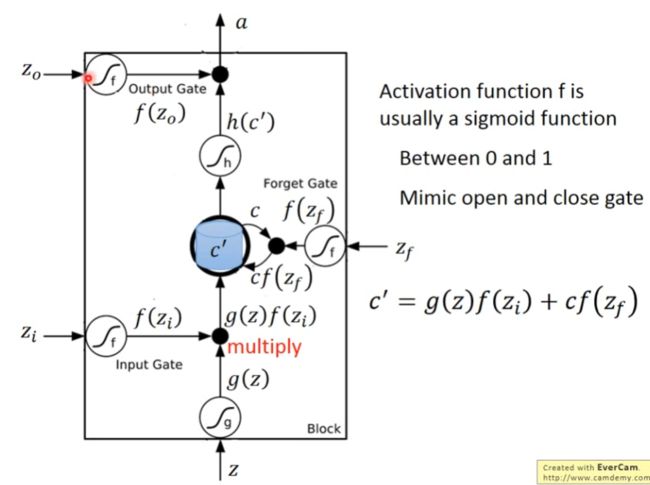
其计算方式如下图:
LSTM相当于在模拟人脑记忆,Input Gate就是当前知识你记住了多少,Forget Gate就是原有的知识你还记住多少,Output Gate就是你最终记住了多少知识。
Transformer
参考文章:Transformer模型详解
自监督学习(Self-Supervised Learning)
一般机器学习分为有监督学习,无监督学习和强化学习。 而 Self-Supervised Learning 是无监督学习里面的一种,主要是希望能够学习到一种通用的特征表达用于下游任务 (Downstream Tasks)。
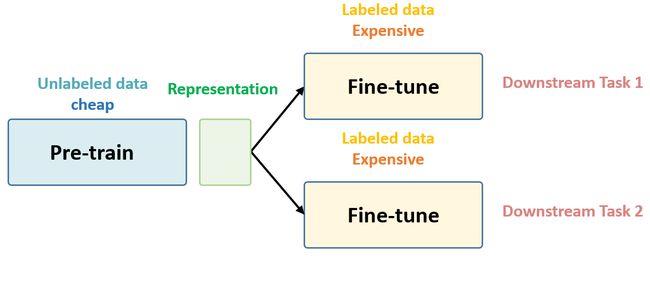
Self-Supervised Learning工作流程如如下图所示:
Self-Supervised Learning分为两个阶段,第一个阶段不涉及任何下游任务,就是拿着一堆无标签的数据去预训练,没有特定的任务;第二个阶段涉及下游任务,就是拿着一堆带标签的数据去在下游任务上 进行微调(Fine-tune)。参考文章:Self-Supervised Learning 超详细解读
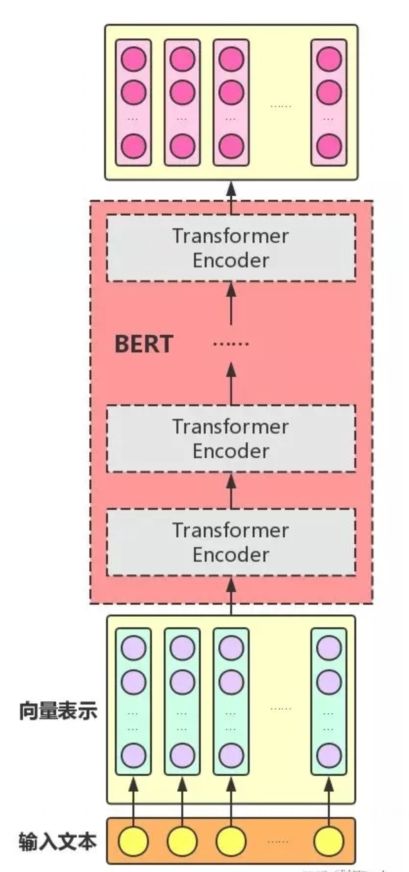
BERT
BERT的结构与Transformer的Encoder模块类似,如下图所示:
BERT主要任务为预训练(Pre-train)和微调(Fine-tune)。
预训练(Pre-train)
预训练(Pre-train)阶段有两个预训练任务:Masked LM和Next Sentence Prediction。
Mask LM
Mask LM通俗地说就是在输入一句话的时候,随机地选一些要预测的词,然后用一个特殊的符号[MASK]来遮盖住它们,之后让模型根据所给的标签去学习这些地方该填的词。
如下图所示,有w1、w2、w3、w4四个输入,利用特殊的符号[MASK]遮盖w2,让Bert模型根据其他的输入来预测w2。
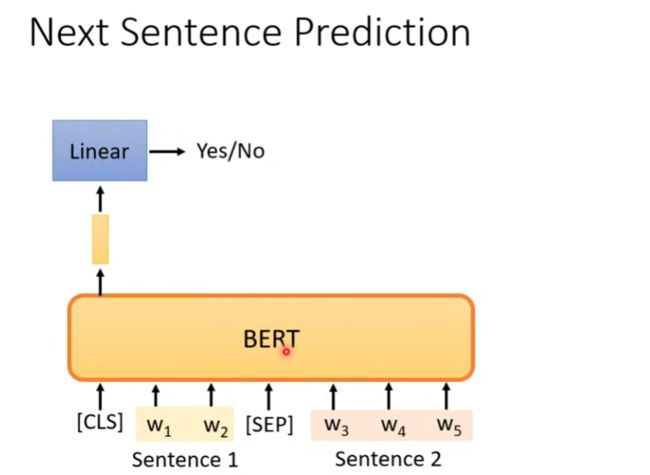
Next Sentence Prediction
Next Sentence Prediction就是预测输入BERT的两段文本是否为连续的文本,引入这个任务可以更好地让模型学到连续的文本片段之间的关系。在有些任务中,比如问答,前后两个句子有一定的关联关系,我们希望BERT模型在Pre-train阶段能够学习到这种关系。
如下图所示,有sentence1、sentence2两个句子,我们用符号[SEQ]把它们隔开,在最前方加入一个特殊Token [CLS],利用它的输出接上Linear进行分类,预测sentence1、sentence2是否为连续的文本。
微调(Fine-tune)
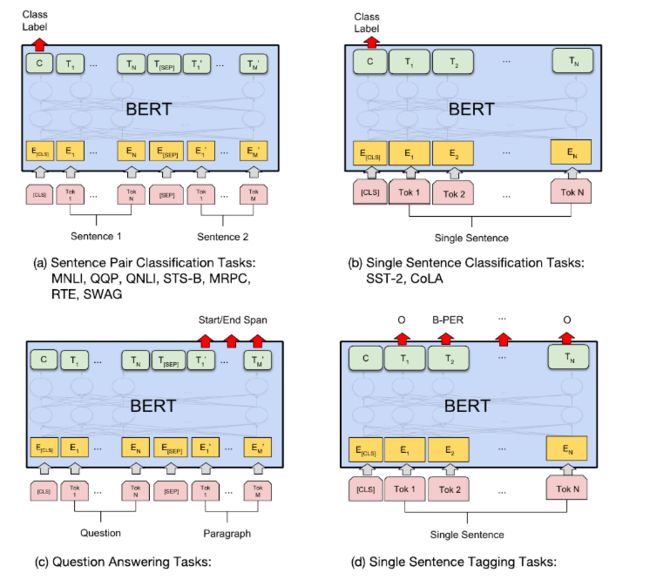
BERT的Fine-Tuning如下图所示,共分为4类任务。
(1)对于相似度计算等输入为两个序列的任务,如图左上所示,我们在最前方加入一个特殊Token [CLS],利用它最后一层输出接上softmax进行分类,然后用分类数据进行Fine-Tune。
(2)对于普通的分类任务,如图右上所示,输入是一个序列,我们在最前方加入一个特殊Token [CLS],利用它最后一层输出接上softmax进行分类,用分类的数据来进行Fine-Tune。
(3)对于问答类任务,如图左下所示,输入是一个问题和一段很长的包含答案的文字(Paragraph),输出在这段文字里找到问题的答案,答案是Paragraph里的一段连续的文字(Span)。BERT把寻找答案的问题转化成寻找这个Span的开始下标和结束下标的问题。
如下图所示,将两个特殊的向量与Bert模型的输出进行点乘(Dot Product)的结果接上softmax进行分类,找到这个Span的开始下标s和结束下标e。
(4)对于序列标注任务,比如命名实体识别,如图右下所示,输入是一个句子(Token序列),除了[CLS]和[SEP]的每个时刻都会有输出的Tag,我们可以利用用输出的Tag来进行Fine-Tune。
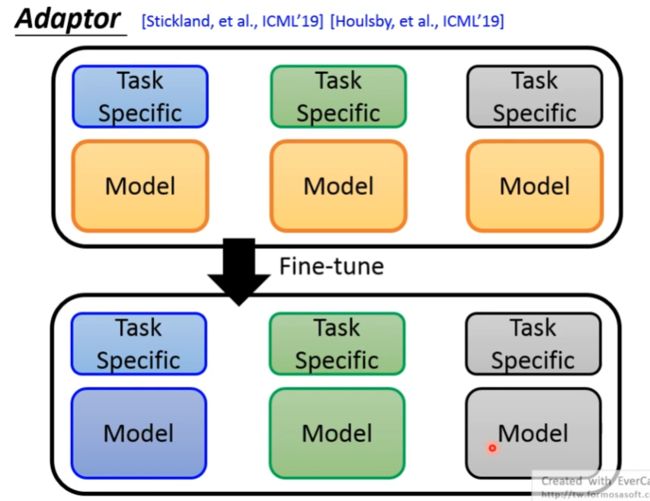
如下图所示,为了解决不同的任务,需要对Bert模型进行微调(Fine-tune),但是Bert模型是很大的,按照如下图中的步骤进行Fine-tune,或许是行不通的。
针对这一问题,可以在模型中加入Adaptor,只对Adaptor进行微调(Fine-tune)就可以了。
参考文章:Bert模型详解