深大算法实验六——最大流应用问题

代码链接：深大算法实验六——最大流问题-C++文档类资源-CSDN下载

 

目录

一. 问题描述

二. 构建流网络

三. 求解过程

四.  Ford-Fulkerson方法

1. 残留网络

2. 割

五. Dinic算法

六. Dinic＋多路增广

七. ISAP

数据分析：

Dinic算法：

多路增广Dinic算法

ISAP算法

改变论文数目

改变评委数目

改变a的值

改变b的值

实验结论：

---

一. 问题描述

1. 有m篇论文和n个评审，每篇论文需要安排a个评审，每个评审最多评b篇论文。请设计一个论文分配方案。

2. 要求应用最大流解决上述问题，画出m=10，n=3的流网络图并解释说明流网络图与论文评审问题的关系。

3. 编程实现所设计算法，计算a和b取不同值情况下的分配方案，如果没有可行方案则输出无解。

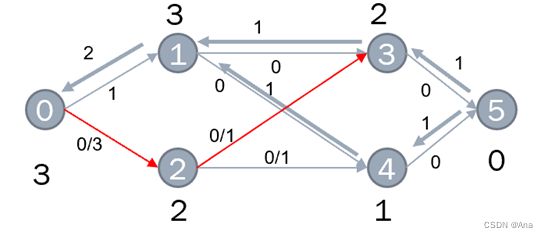
二. 构建流网络

        我们可以将问题抽象成每一个评审和论文是一个节点，将每个评审最多评的论文数量作为评审的入度，也就是说评审节点最多承载b单位的流，每个论文需要多少评审作为论文节点的出度，也就是说每篇论文需要a单位的流。再加上首位两端的起点和汇点即可生成流网络。

       中间的蓝色边的权值全部为1，代表每个评审都可以选择所有的论文。

 

三. 求解过程

        

将使用FF方法来寻找此流网络的最大流。若最大流可以等于说明存在分配方案，若小于则说明还有论文没有被批完，则没有存在可行的分配方案。在进行寻找最大流时进行寻找分配方案。

        由于在用FF方法时需要使用DFS进行查找最短增广路径，在查找时若遇到评委节点指向论文节点的化，就记录下其边。

四.  Ford-Fulkerson方法

       F-F方法是一种解决最大流的一种方法，之所以称之为方法而不是算法是因为其实现算法有很多种。

       F-F方法的最重要的三个思想是：残留网络、增广路径和割。

       F-F方法的过程是：

1. 1. 1. 找到一条增广路径
      2. 求出这条路径的最大流（即看这条路径的最小权值）
      3. 更新权值并起来画出其残留网络
      4. 在残留网络中继续寻找增广路径
      5. 重复1、2、3、4直到没有增广路径到汇点

F-F方法的基本伪代码：

Ford-Fulkerson方法(G,s,t)
初始化流f为0
While(存在一条增广路径p) {
沿着增广路径p增广流f
}
返回f

1. 残留网络

残留网络是更新权值时，增加一条反向边，反向边的值即为通过该边的流的大小。

        如上图，该边的值为14，通过的流大小是11，更新权值后并且更新成残留网络后，反向边权值为11，正向边为3。

2. 割

       割是可以将流网络分解成两个区域，每个区域都可以看作为一个节点。

 

如图所示，该流网络可以看作为两个节点。割的净流为

。割的容量为。

       求最大径流量就是求其流网络的最小割。

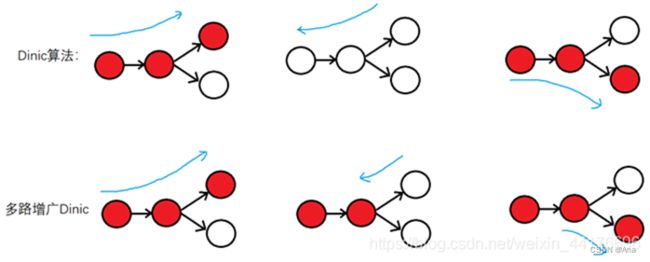
五. Dinic算法

       Dinic算法是先使用BFS将流网络进行分层，这样可以避免进行DFS寻找增广路径时出现重复的情况。

 

       在进行DFS寻找增广路径时，下一节点必定在此节点的下一层。

DFS伪代码：

	DFS(x, flow)
		if x==汇点
			return flow
		for y in 邻接[x]
			fxy = 边xy允许的流量最大值
			r = DFS(y, min(flow, fxy))
			if r≠ 0
				更新边xy的权值
				return r
		return 0

       在DFS完毕之后再次使用BFS对残留网络重新进行分层

Dinic算法伪代码：

	while true
		flag = BFS()
		if  !flag
			break
		while true
			r = DFS(起点, infinity)
			if r = 0
				break

Dinic算法效率分析：

       因为dinic的dfs按照层次来递归，因为每次扫描出的层数是递增的，而且不超过n，所以外循环bfs最多进行n次，而因为每次找增广路都有一条边作为“瓶颈”，一共有e条边，就有e个瓶颈，e条路径，要进行e次dfs，每次dfs复杂度为，总体复杂度为

六. Dinic＋多路增广

        由于Dinic算法在进行DFS寻找增广路径时，找到一个增广路径以后就直接退回到起点，再进行寻找另外的增广路径，这样会大大的降低效率，于是提出了一个多路增广的思想，就是遍历到一个增广路径之后，只返回到上一父亲节点，再向下寻找增广路径。这样子一次DFS就可以寻找到多条增广路径。

        多路增广DFS伪代码：

DFS()
	If x=汇点
		return flow
	temp = flow
	for y in邻接 [x]
		fxy = 边xy的权值
		r = DFS(y, min(flow, fxy))
		if r≠ 0
			更新边xy的权值
			flow = flow – r
			if  flow = 0
			return r
	return 0

多路增广Dinic复杂度分析：

外循环同样是每次bfs扫描层次，最多做n次bfs。

而每次内循环都做一次dfs，需要注意这里的dfs不带访问控制数组，只要有边就能过，这意味着每一个节点可以多次被经过，所以dfs复杂度不是

因为最多存在e条最短增广路径，而每次走到汇点至多走n步，所以dfs的代价是，这使得多路增广Dinic的总体复杂度是

七. ISAP

       ISAP大体上与多路增广Dinic相同，只是在进行DFS寻找增广路径时动态的更新残留网络的层的值。

       ISAP只需要进行一次BFS，并且还引入了一个优化，如果某一层的节点数为0，则说明已经没有了增广路径，可以直接跳出。

       关于如何动态更新层可以用以下例子举例

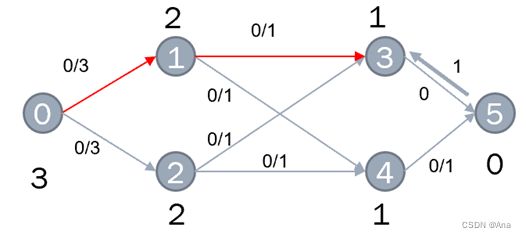
        1. 首先进行一次BFS赋予流网络关系，并且将层次关系反向。

 

 

        2. 找到一条增广路径并且更新其增广路径

        3. 退栈时，若该边仍然由路径可走，则将其层次加1

        4. 若遇到死路，则将此节点层次加1。

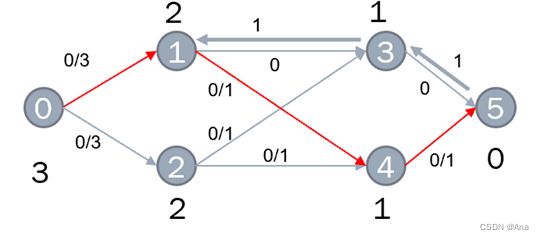
                 此时找到了一条增广路径。

 更新其残留网络，因为(1,3)边没有剩余权值，所以节点3的边关系无需改变。这是因为若(3,5)边还有剩余值时，还可以从另外的路径到节点3，所以此时无需改变其层次。

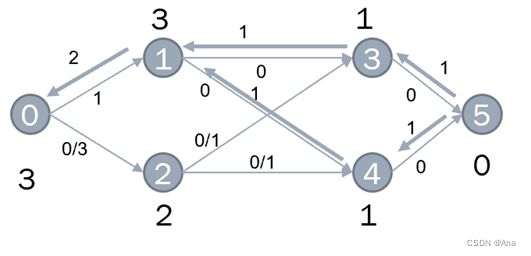
 根据多路增广Dinic算法的DFS遍历，则会选择上面的增广路径。

               同样的更新其残留网络。

              到节点1处，由于(0,1)边还有剩余的残量，这说明了从节点1这条路走已经没               有增广路径了，从而将其层次改变成3。

 

接下来从此路径走，此时会发现已经是一条思路，所以将3节点的层次改变成2。 

ISAP算法效率分析：

       和多路增广Dinic算法中的DFS一样，复杂度是，原因也是不带访问控制数组，一个节点会被多次访问，最多有e条增广路径，而每次需要走过n个点到达汇点，所以复杂度，因为外循环需要判断源点的高度，而源点最多增高n次，总体复杂度为。

数据分析：

• Dinic算法：

()

	时间		时间
100	0.01	600	2.961
200	0.08	700	5.025
300	0.302	800	7.725
400	0.712	900	10.765
500	1.541	1000	15.378

 

• 多路增广Dinic算法

( )

	时间		时间
100	0.005	600	1.333
200	0.031	700	2.491
300	0.111	800	4.511
400	0.416	900	6.422
500	0.703	1000	8.662

• ISAP算法

()

 

	时间		时间
100	0.007	600	1.274
200	0.057	700	2.452
300	0.166	800	4.141
400	0.317	900	6.538
500	0.68	1000	8.49

        综上可以看出多路增广Dinic和ISAP算法都要比Dinic算法快，当时两者相差的时间并不是特别大，也许是因为该测试数据无需进行多次层次调整导致的。

• 改变论文数目

（n=150，a=150，b=300）

由于Dinic算法与另外两个有较大的差别，所以接下来先实另外两种算法的图表对比。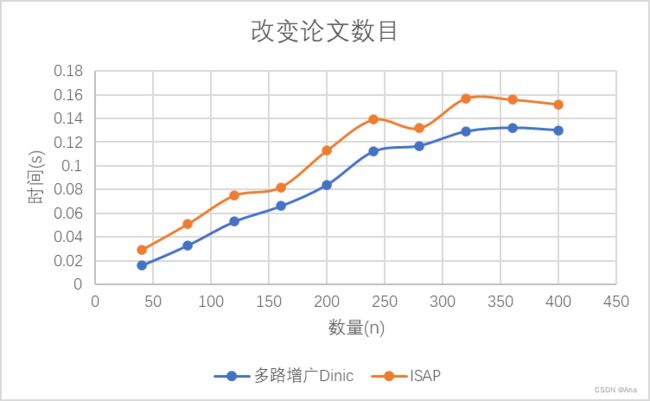 

 更好用上面两个图可以发现Dinic算法在M小于300时所用的时间是十分多的，这是因为当M大于300时只用做一次BFS就可以找到最大流，e次DFS。而在多路增广Dinic和ISAP种多路增广Dinic算法是比ISAP要快的。

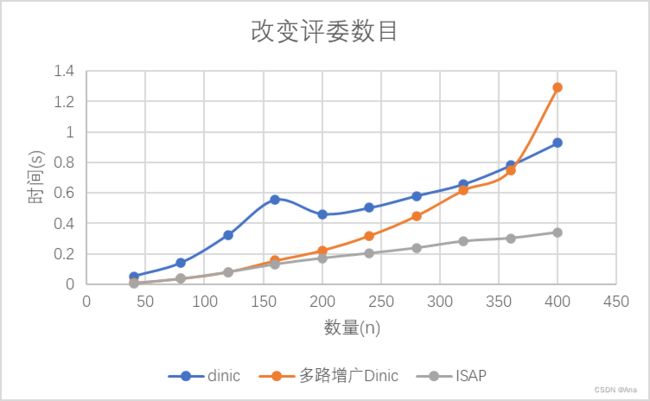
• 改变评委数目

（m=300， a=150，b=300）

• 改变a的值

（m=300， n=150，b=300）

 

 

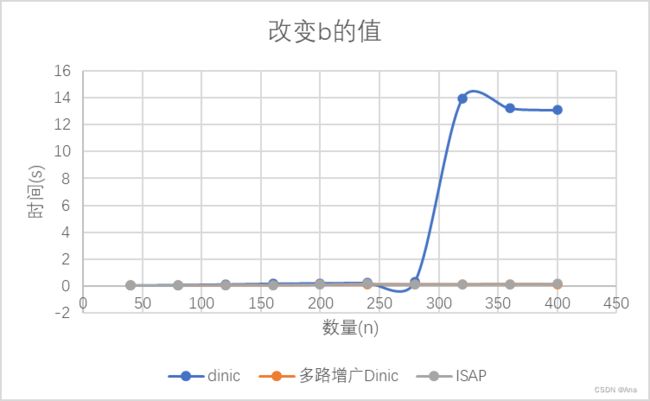
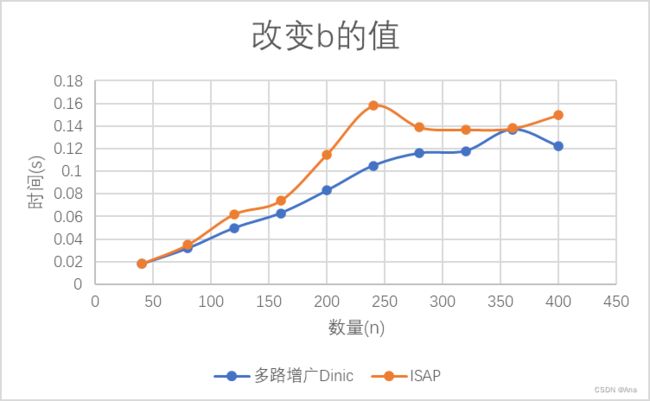
• 改变b的值

 只对比多路增广Dinic和ISAP

       我们可以很明显的看到当Dinic算法超过300时，需要用很多的时间，这与第一个改变论文数目的突变的原因是一样的。

       从上述图像可以看出来，当改变论文数目、评委数目和评委最多改多少论文对时间是有关联的。对于Dinic算法来说，当没有答案的时候时间会十分的快，有答案时需要的时间会比较长。

 

实验结论：

       本次实验完成了求最大流的算法，并且求出了求最大流的算法效率。从上述可知多路增广Dinic算法和ISAP算法是比较快的两种算法。对于要更新多次层次的话ISAP算法理论上会比多路增广更快一些。

       本次实验还让我门体会了如何将复杂的问题抽象化，并且转换成相应的算法样例去解决。