集合类状压dp：AcWing 91. 最短Hamilton路径

前置位运算知识

与 and, &：1 & 1 = 1，0 & 1 = 0，0 & 0 = 0；（联想电路串联）
或 or, l：1 | 1 = 1，0 | 1 = 1，0 | 0 = 0；（联想电路并联）
非 not, ~：not 1 = 0，not 0 = 1；
异或 xor（写代码的时候用 “^” 表示）：1 xor 1 = 0，0 xor 1 = 1，0 xor 0 = 0；（俗称 不进位加法：相同得 0，相异得 1）

在 m 位二进制数 中，为方便起见，通常称 最低位为第 0 位，从右到左 依此类推，最高位 为 第 m-1 位。

移位运算

左移：在 二进制表示 下，把数字 同时向左移动，低位以 0 填充，高位越界后舍弃。

1 << n = 2^n，n << 1 = 2n（左移几位就向末尾补几个 0，比如 11，左移 1 位 <<1 变成 110，左移 2 位 <<2 变成 1100，以此类推）

算术右移：在 二进制补码表示 下，把数字 同时向右移动，高位以符号位填充，低位越界后舍弃。

n >> 1 = n / 2.0（右移几位就删除几个末尾元素，比如 1110101，右移 1 位 >>1 变成 111010，右移 2 位 >>2 变成 11101，以此类推）

算术右移 等于 除以 2 向下取整，(-3) >> 1 = -1，3 >> 1 = 1。

二进制状态压缩

二进制状态压缩，是指将一个 长度为 m 的 bool 数组 用一个 m 位二进制整数 表示并存储的方法。

利用下列 位运算操作 可以实现 原 bool 数组中 对应下标元素 的存取。（注意下面的“第 k 位”是指 下标从 0 开始计数）

• 操作：取出整数 n 在二进制表示下的第 k 位。 运算：(n >> k) & 1；
• 操作：取出整数 n 在二进制表示下的第 0～k -1 位(后 k 位)。 运算：n & ((1 << k) - 1)；
• 操作：把整数 n 在二进制表示下的第 k 位取反。 运算：n xor (1 << k)；
• 操作：对整数 n 在二进制表示下的第 k 位赋值 1 。 运算：n | (1 << k)；
• 操作：对整数 n 在二进制表示下的第 k 位赋值 0。 运算：n & (~(1 << k))；

这种方法运算简便，并且 节省了程序运行的时间和空间。

当 m 不太大 时，可以 直接使用一个整数类型存储。

当 m 较大 时，可以使用 若干个整数类型( int 数组)，也可以直接利用 C++ STL 为我们提供的 bitset 实现。

状态压缩dp

在 线性 DP 中，我们提到，动态规划的过程是随着“阶段”的增长，在 每个状态维度上不断扩展 。

在任意时刻，已经求出最优解的状态 与 尚未求出最优解的状态 在各维度上的分界点组成了 DP扩展的“轮廓”。

对于某些问题，我们需要 在动态规划的“状态”中记录一个集合，保存这个 “轮廓”的详细信息，以便进行 状态转移。

若 集合大小 不超过 N ，集合中 每个元素都是小于 K 的自然数，则我们可以把这个集合看作一个 N 位 K 进制数，以一个 [0, K^N - 1] 之间的十进制整数的形式 作为 DP 状态的一维（核心要义）。

这种 把集合转化为整数 记录在 DP 状态中的一类算法，被称为：状态压缩动态规划 算法。

接下来的例题 “AcWing 91. 最短Hamilton路径” 向我们展示了简单的 状态压缩DP 思想。

例题：AcWing 91. 最短Hamilton路径

题意：

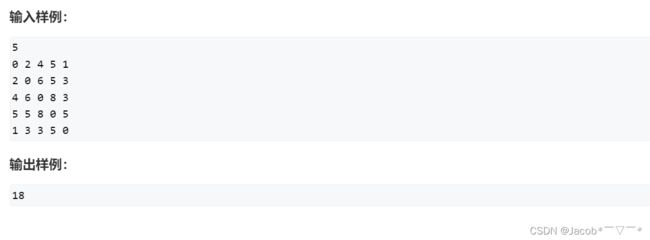
给定一张 n (n ≤ 20) 个点的 带权无向图，点从 0~n-1 标号，求起点 0 到终点 n - 1 的最短Hamilton路径。

Hamilton路径的定义：从 0 到 n-1 不重不漏地经过每个点恰好一次。

思路：

如果用纯暴力的话，时间复杂度为O(n*n!)，n<=20，这样肯定会超时，我们考虑用状态压缩dp求解。

本题核心即为状压dp的思想，用一个整数来表示一个状态。

f[i, j]状态表示：

我们发现每个点遍历的顺序我们是不关心的，只注意两方面：

• ① 哪些点被遍历过（且每个点有且只被遍历一次）
• ② 目前停在了哪一个点上

这两方面能唯一确定当前搜索的状态是什么

集合：所有从 0 走到 j，中间所有点是 i （走过的所有点存于整数 i 当中）的所有路径（每个点只能走一次）

i 即表示一个压缩的状态，要看作一个二进制数，这个二进制数中每一位分别表示 当前这个点是否走过。

举个例子，如果 i = (1110011)，表示第0、1、4、5、6个点都已经走过了

属性：最小值min

f[i, j]状态计算：

集合划分：以走过的 倒数第 2 个点是哪一个 进行划分，显然 倒数第 2 个点 有 n 种情况：0、1、2、...、n-1。

如果倒数第 2 个点是 k 的话，即从起点 0 根据某一可能的路线先走到 k， 最后一步从 k 走到 j，

我们来分析一下：首先最后一步是已知的，即为 k -> j 对应的权值，若要使得整个路径最短，我们 只需使得 0 -> k 这段路径最短即可，

从 0 -> j 走过的所有点 用 i 表示，那么 从 0 -> k 走过的所有点 即在 i 表示的状态基础上除去 j 点（f[i - {j}, k]）

粗略表示一下：从 0 -> j 的最短路径为 f[i - {j}, k] + weight[k, j]。

f[i, j] 的计算：对所有 k （k = 0, 1, ..., n-1）的情况取最小值即可。

时间复杂度：

第一维表示哪些点被遍历过，共有 2 种情况： 用 or 不用，共 20 个点，共 2^20 种情况

第二维表示目前停在哪个点，共 20 种情况

总状态数量为两维相乘： 2^20 * 20 = 2e7

状态数量（2e7） × 状态转移（20）约等于 4e8，本题时限为 5s ，计算量最多 5e8，所以是合法的。

细节：

我们应当外层循环路径 i ，内层循环终点 j ，这样能保证 dp 状态是按照拓扑序来计算的，状态转移需要的状态必须被提前计算出来才行。

代码：

#include

using namespace std;
const int N = 20;
int dp[1<>n;
    for(int i=0; i>w[i][j];
    
    memset(dp, 0x3f, sizeof dp); //正无穷
    dp[1][0] = 0; //初始时，位于 0 号点，相当于从 0 走到 0，走过的点只有 0 这一个点，即第 0 位是 1，其余为 0
    for(int i=0; i<1<>j&1) //因为是从 0 走到 j，那么 i 这个状态肯定要包含 j，这样才有意义
            {
                for(int k=0; k>k&1) //如果是从 k 点转移而来，那么当前枚举的 i 除去 j 点之后一定要包含 k 点（参考本篇开头的公式），当然也可以写成：(i-(1<>k&1
                    {
                        dp[i][j] = min(dp[i][j], dp[i & (~(1 << j))][k] + w[k][j]);
                    }
                }
            }
        }
    }
    cout<