【题解】CSP-J2021第二轮题解

CSP-J2021第二轮题解

T1.分糖果 $\otimes$

简化题目：给定 $l,r$，求 ${\max }_{i=l}^r(i\mathrm{mod}n)$。
分类讨论，根据 $\lfloor \frac{i}{n}\rfloor$ 将整数分组，若 $l$ 与 $r$ 在同一组中，那么答案为 $r\mathrm{mod}n$；否则，答案为 $n-1$。具体见下图。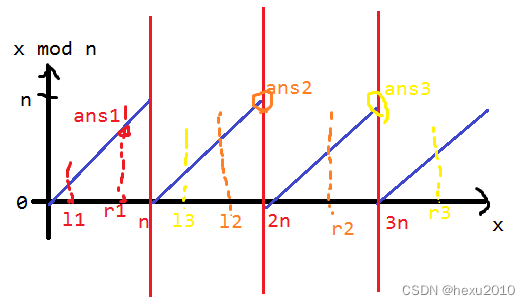

T2.插入排序 $\otimes$

这是一道插入排序的好题，从插入排序的基本思想上出，确实是“更好地理解插入排序”。
插入排序的思想：设原序列为 $a_i$，则插入排序函数 $f(1\sim n)$ 的实现方法就是先处理好 $f(1\sim n-1)$ 的部分，在将 $a_n$ 放到合适的位置。过程如下：
a = {[1],4,2,8,5,7} $\Rightarrow$ a = {[1,4],2,8,5,7} $\Rightarrow$ a = {[1,2,4],8,5,7} $\Rightarrow$
a = {[1,2,4,8],5,7} $\Rightarrow$ a = {[1,2,4,5,8],7} $\Rightarrow$ a = {[1,2,4,5,7,8]}
故其为 $O(n^2)$ 的算法。我们还要结合题目中给的代码分析一下排序的性质：

for (int i = 1; i <= n; i++)
	for (int j = i; j >= 2; j--)
		if (a[j] < a[j-1]) {
			int t = a[j-1];
			a[j-1] = a[j];
			a[j] = t;
		}

这份代码的排序方式：1.从小到大排列。2.碰到相同的数时，原序列中位置靠前的在前面。
一些基本的东西终于讲完了，现在针对这道题讲一下啊。首先根据排序方式的第二点，可以得出整道题我们要将一个数的位置和值绑在一起，即一个形如 $(a_i,i)$ 的 pair 。根据 pair 的优先级，在比较整个 pair 时会先比较 $a_i$ 的值，再比较 $i$ 的值。接下来，在针对操作讲一下。从复杂度的角度来看，$n⩽5000,Q⩽200000$，每个操作所给的时间并不多。但是，做题的时候，要注意——**看题！**题目中说，操作 $1$ 的个数不超过 5000，说明操作一的复杂度可以放宽来，$O(n)$ 刚刚好。由此还可以得知操作二的复杂度就是 $O(1)$。假如没有操作一，这题非常简单，有了操作一之后，维护 $p[i]$ 表示原序列第 $x$ 个数现在所处位置即可。
接下来，这道题的精华就出来了——考虑操作一给结果带来的变化。根据插入排序的思想，每一个数都慢慢向前面“漂”过去，整个序列的排序是随着每个数位置的确定而确定。所以，操作一的 $O(n)$ 做法就是让被修改的数找到它的位置。过程中，每一次交换都让两个的 $p$ 值互换。但令人惊奇的是，操作二 $O(n)$ 竟然能过……

T3.网络连接 $\otimes$

大模拟。关于大模拟的题目，洛谷日报有一期专门讲了，还是挺不错的。
网上虽然有用 sscanf 的方法，但是我不太会，考场上也不一定想得到，这里主要讲一下分类讨论和模块化的思想。
模块化能让你的代码少出错，好调试。这里，我们如果编写了一个函数 $\text{check}$，那么主函数的代码将会非常简短，非常好编写，重心全部落在 $\text{check}$ 函数怎么写了。题目中给定的要求是形式为 a.b.c.d:e，$0⩽a,b,c,d⩽255$，$0⩽e⩽65535$。那么，只需要判断两个：1.形式是否合法。2.数字是否符合要求。判断形式是否合法，主要是判断 . 的个数和 : 的个数以及它们的顺序。这里讲几个容易漏的点：注意形如 .9.63.198:8080 和 89..22.198:8080 等，也就是符号的位置不对。判断数字是否符合要求比较简单，不要漏了前导 0 就好了。
这题细节真的是很多，考场上如果不用 sscanf 真的很难 AC，来试一试你能拿多少分吧！

T4.小熊的果篮 $\otimes$

这题主要考察 STL 的运用，还看一点运气。我考试的时候换了好几个方法，结果都没出来。正解是用两个 set，分别记录苹果和橘子的位置。每一次先选择位置最靠前的（min(*st[0].begin(), *st[1].begin())），然后在另一边二分出下一个块的位置。这里主要是因为苹果块和橘子块是互相交织的，所以苹果的位置中第一个大于当前橘子位置的那个位置就是下一个块的开头。其他的话，还有一个小技巧，就是在操作之前提前放入 INF，方便判断苹果和橘子是不是没了，最后记得把剩余的水果都输出一下，具体见代码。

代码

T1

#include 
#define int long long
using namespace std;
inline int read(){
	int s = 0, w = 1;
	char ch = getchar();
	for(; ch < '0' || ch > '9'; w *= ch == '-' ? -1 : 1, ch = getchar());
	for(; ch >= '0' && ch <= '9'; s = 10 * s + ch - '0', ch = getchar());
	return s * w;
}
signed main(){
	int n = read(), l = read(), r = read(), base = l % n, ans = base;
	if(l / n != r / n){
		cout << n - 1 << endl;
	} else {
		cout << r % n << endl;
	}
	return 0;
}

T2

#include 
#define int long long
using namespace std;
inline int read(){
	int s = 0, w = 1;
	char ch = getchar();
	for(; ch < '0' || ch > '9'; w *= ch == '-' ? -1 : 1, ch = getchar());
	for(; ch >= '0' && ch <= '9'; s = 10 * s + ch - '0', ch = getchar());
	return s * w;
}
const int MAXN = 8005;
int n, T;
pair<int, int> a[MAXN];
signed main(){
//	freopen("sort4.in", "r", stdin);
//	freopen("sort4.out", "w", stdout);
	n = read(), T = read();
	for(int i = 1; i <= n; i++){
		a[i].first = read();
		a[i].second = i;
	}
	sort(a + 1, a + 1 + n);
	for(int _ = 1, op; _ <= T; _++){
//		cout << "Round " << _ << ":" << endl;
		op = read();
		if(op == 1){
			int pos = -1, x = read(), v = read();
			for(int i = 1; i <= n; i++){
				if(a[i].second == x){
					pos = i;
					break;
				}
			}
			a[pos].first = v;
			while(pos < n && a[pos] > a[pos + 1]){
				swap(a[pos], a[pos + 1]);
				pos++;
			}
//			cout << endl;
//			for(int i = 1; i <= n; i++){
//				cout << a[i].first << " " << a[i].second << endl;
//			}
			while(pos > 1 && a[pos] < a[pos - 1]){
				swap(a[pos], a[pos - 1]);
				pos--;
			}
//			cout << endl;
//			for(int i = 1; i <= n; i++){
//				cout << a[i].first << " " << a[i].second << endl;
//			}
		} else if (op == 2){
			int x = read();
			for(int i = 1; i <= n; i++){
				if(a[i].second == x) {
					cout << i << endl;
					break;
				}
			}
//			cout << endl;
//			for(int i = 1; i <= n; i++){
//				cout << a[i].first << " " << a[i].second << endl;
//			}
		}
	}
	return 0;
}

T3

#include 
#define int long long
using namespace std;
inline int read(){
	int s = 0, w = 1;
	char ch = getchar();
	for(; ch < '0' || ch > '9'; w *= ch == '-' ? -1 : 1, ch = getchar());
	for(; ch >= '0' && ch <= '9'; s = 10 * s + ch - '0', ch = getchar());
	return s * w;
}
const int MAXN = 1005;
string cl[MAXN];
int check_int(string s){
	if(s.size() == 0) return -1;
	if(s.size() == 1) return s[0] - '0';
	if(s[0] == '0') return -1;
	int res = 0;
	for(int i = 0; i < s.size(); i++){
		res = res * 10 + s[i] - '0';
	}
	return res;
}
bool check(string s){
	int cntdot = 0, cntdots = 0;
	for(int i = 0; i < s.size(); i++){
		cntdot += (s[i] == '.');
		cntdots += (s[i] == ':');
	}
	if(cntdot != 3 || cntdots != 1) return false;
	int l = 0;
	bool flag = false;
	if(s[0] == '.') return false;
	for(int i = 1, tmp; i < s.size(); i++){
		if(s[i] == '.' || s[i] == ':'){
			if(s[i - 1] == '.' || s[i - 1] == ':') return false;
			if(s[i] == ':') flag = true;
			if(flag && s[i] == '.') return false;
			tmp = check_int(s.substr(l, i - l));
			if(tmp == -1) return false;
			if(tmp >= 256) return false;
			l = i + 1;
		}
	}
	int tmp = check_int(s.substr(l, s.size() - l + 1));
	if(tmp < 0 || tmp > 65535) return false;
	return true;
}
signed main(){
//	freopen("P7911_14.in", "r", stdin);
//	freopen("P7911_14.user", "w", stdout);
	int n = read(), tot = 0;
	string tmp;
	for(int i = 1; i <= n; i++){
		getline(cin, tmp);
		string s = tmp.substr(7, tmp.size() - 7);
		if(check(s) == false){
			cout << "ERR" << endl;
			continue;
		}
		if(tmp.substr(0, 6) == "Server"){
			bool flag = true;
			for(int j = 1; j < i; j++){
				if(cl[j] == s){
					cout << "FAIL" << endl;
					flag = false;
					break;
				}
			}
			if(flag){
				cout << "OK" << endl;
				cl[i] = s;
			}
		} else {
			bool flag = true;
			for(int j = 1; j < i; j++){
				if(cl[j] == s){
					cout << j << endl;
					flag = false;
					break; 
				}
			}
			if(flag) cout << "FAIL" << endl;
		}
	}
	return 0;
}

T4

#include 
#define int long long
using namespace std;
inline int read(){
	int s = 0, w = 1;
	char ch = getchar();
	for(; ch < '0' || ch > '9'; w *= ch == '-' ? -1 : 1, ch = getchar());
	for(; ch >= '0' && ch <= '9'; s = 10 * s + ch - '0', ch = getchar());
	return s * w;
}
set<int> st[2];
signed main(){
	int n = read();
	for(int i = 1; i <= n; i++){
		st[read()].insert(i);
	}
	for(int i = 0; i < 2; i++){
		for(set<int>::iterator it = st[i].begin(); it != st[i].end(); it++){
			cout << *it << " ";
		}
		cout << endl;
	}
	while(!st[0].empty() && !st[1].empty()){
		set<pair<int, int> > out;
		for(int d = 0, lst; d < 2; d++){
			lst = *st[d].begin();
			out.insert(make_pair(lst, d));
			for(set<int>::iterator it = ++st[d].begin(); it != st[d].end(); it++){
				if(lst + 1 < *it) out.insert(make_pair(*it, d));
//				cout << lst << " " << *it << endl;
				lst = *it;
			}
		}
		for(set<pair<int, int> >::iterator it = out.begin(); it != out.end(); it++){
			cout << it->first << " ";
			st[it->second].erase(it->first);
		}
		cout << endl;
	}
	return 0;
}

后记

我整理了一下 $\text{CSP-J2019}\sim \text{2021}$ 的题目难度（以洛谷为主）：

$年份$	$\text{T1}$	$\text{T2}$	$\text{T3}$	$\text{T4}$
$\text{2019}$	$\text{入门}$	$\text{普及-}$	$\text{普及}$	$\text{普及}$
$\text{2020}$	$\text{入门}$	$\text{普及-}$	$\text{普及}$	$\text{普及}$
$\text{2021}$	$\text{入门}$	$\text{普及-}$	$\text{普及}$	$\text{普及}$

可以发现题目是越来越简单了，但是越简单的题目越是要得分，这样子才有机会拿到省一。