2021-10-17周总结(复盘)
一、信息学oj-1331:【例1-2】后缀表达式的值
(1)问题描述
从键盘读入一个后缀表达式(字符串),只含有0-9组成的运算数及加(+)、减(—)、乘(*)、除(/)四种运算符。每个运算数之间用一个空格隔开,不需要判断给你的表达式是否合法。以@作为结束标志。
比如,16–9*(4+3)转换成后缀表达式为:16□9□4□3□+*–,在字符数组A中的形式为:
![]()
栈中的变化情况:
![]()
运行结果:-47
提示:输入字符串长度小于250,参与运算的整数及结果之绝对值均在264264范围内,如有除法保证能整除。
【输入】
一个后缀表达式。
【输出】
一个后缀表达式的值。
(2)问题分析
这道题的做法完完全全应用了栈的性质,总体来说很好实现(相比于中缀表达式),主要是将数字和符号入栈,碰到符号弹栈两个数字计算后一起入栈。
(3)代码实现
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
int main(){
ll s=0,y=0,x=0;
stackn;
char ch;
while(ch!='@')
{
ch=getchar();
switch(ch){
case '+':y=n.top();n.pop();x=n.top();n.pop();n.push(x+y);break;
case '-':y=n.top();n.pop();x=n.top();n.pop();n.push(x-y);break;
case '*':y=n.top();n.pop();x=n.top();n.pop();n.push(x*y);break;
case '/':y=n.top();n.pop();x=n.top();n.pop();n.push(x/y);break;
case ' ':n.push(s);s=0; break;
default:s=s*10+ch-'0';break;
}
}
printf("%lld",n.top());
return 0;
} (2)信息学oj-1354:括弧匹配检验
(1)问题描述
假设表达式中允许包含两种括号:圆括号和方括号,其嵌套的顺序随意,如([ ]())或[([ ][ ])]等为正确的匹配,[( ])或([ ]( )或 ( ( ) ) )均为错误的匹配。
现在的问题是,要求检验一个给定表达式中的括弧是否正确匹配?
输入一个只包含圆括号和方括号的字符串,判断字符串中的括号是否匹配,匹配就输出 “OK” ,不匹配就输出“Wrong”。输入一个字符串:[([][])],输出:OK。
【输入】
输入仅一行字符(字符个数小于255255)。
【输出】
匹配就输出 “OK” ,不匹配就输出“Wrong”。
【输入样例】
[(])
【输出样例】
Wrong
(2)问题分析
这道题不算很复杂,碰到[和(就入栈,如果碰到]判断栈是否为空,如果栈不为空判断栈顶是否是[否则就输出NO同理栈为空也输出NO,(同理判断.
(3)代码实现
#include
using namespace std;
stack a;
int main(){
string s;
cin>>s;
for(int i=0;s[i];i++){
if(s[i]=='('||s[i]=='['){
a.push(s[i]);
}else if(s[i]==']'||s[i]==')'){
if(!a.empty()){
if(s[i]==']'){
if(a.top()!='['){
cout<<"Wrong"< 三、信息学oj-1355:字符串匹配问题(strs)
(1)问题描述
字符串中只含有括号 (),[],<>,{},判断输入的字符串中括号是否匹配。如果括号有互相包含的形式,从内到外必须是<>,(),[],{},例如。输入: [()] 输出:YES,而输入([]),([)]都应该输出NO。
【输入】
第一行为一个整数nn,表示以下有多少个由括好组成的字符串。接下来的nn行,每行都是一个由括号组成的长度不超过255255的字符串。
【输出】
在输出文件中有nn行,每行都是YES或NO。
【输入样例】
5
{}{}<><>()()[][]
{{}}{{}}<<>><<>>(())(())[[]][[]]
{{}}{{}}<<>><<>>(())(())[[]][[]]
{<>}{[]}<<<>><<>>>((<>))(())[[(<>)]][[]]
><}{{[]}<<<>><<>>>((<>))(())[[(<>)]][[]]
【输出样例】
YES
YES
YES
YES
NO
(2)问题分析
这三道题推荐一起看,这三题主要是由浅入深,由简单到困难,做这道题的由两个坑,输入字符串的时候不是一个一个输入,而是一起输入,所以这就要判断栈是否是空,字符串也需要重新输入,所以上一回的字符串需要重新清空。
(3)代码实现
#include
using namespace std;
stackq;
int main()
{
int n;
cin>>n;
while(n--){
bool flag=true;
string s;
s.clear();
cin>>s;
while(!q.empty()){
q.pop();
}
for(int i=0;s[i];i++){
if(s[i]=='<'){
q.push(s[i]);
}
else if(s[i]=='('){
if(!q.empty()){
if(q.top()=='<')
flag=false;
else q.push(s[i]);
}
else q.push(s[i]);
}
else if(s[i]=='['){
if(!q.empty()){
if(q.top()=='('||q.top()=='<'){
flag=false;
}
else q.push(s[i]);
}
else q.push(s[i]);
}
else if(s[i]=='{'){
if(!q.empty()){
if(q.top()=='['||q.top()=='('||q.top()=='<'){
flag=false;
}
else q.push(s[i]);
}
else q.push(s[i]);
}
else if(s[i]=='>'){
if(q.empty()){
flag=false;
}
else{
if(q.top()=='<') q.pop();
else flag=false;
}
}
else if(s[i]==')'){
if(q.empty()) flag=false;
else{
if(q.top()=='(') q.pop();
else flag=false;
}
}
else if(s[i]==']'){
if(q.empty()) flag=false;
else{
if(q.top()=='[') q.pop();
else flag=false;
}
}
else if(s[i]=='}'){
if(q.empty()) flag=false;
else{
if(q.top()=='{') q.pop();
else flag=false;
}
}
}
if(q.empty()&&flag) printf("YES\n");
else printf("NO\n");
}
return 0;
} 四、信息学oj-1356:计算(calc)
(1)题目描述
小明在你的帮助下,破密了Ferrari设的密码门,正要往前走,突然又出现了一个密码门,门上有一个算式,其中只有“(”,“)”,“0-9”,“+”,“-”,“*”,“/”,“^”,求出的值就是密码。小明数学学得不好,还需你帮他的忙。(“/”用整数除法)
【输入】
共1行,为一个算式。
【输出】
共1行,就是密码。
【输入样例】
1+(3+2)*(7^2+6*9)/(2)
【输出样例】
258
(2)题目分析
这道题就是中缀表达式的简化版了,因为有加减乘除还有次方,所以要判断优先级顺序,并且还要判断何时入栈出栈,何时计算栈内结果,建立两个栈,一个数字栈,一个符号栈,如果碰到括号,则括号的优先级最大,则数字栈同符号一同出栈计算,并把结果放入栈中.
(3)代码实现
#include
using namespace std;
stackdigit;
stacksymbol;
int level(char c){
if(c=='+'||c=='-') return 1;
if(c=='*'||c=='/') return 2;
if(c=='^') return 3;
return 0;
}
void cal(){
int a=digit.top();
digit.pop();
int b=digit.top();
digit.pop();
char c=symbol.top();
symbol.pop();
if(c=='+') digit.push(b+a);
else if(c=='-') digit.push(b-a);
else if(c=='*') digit.push(b*a);
else if(c=='/') digit.push(b/a);
else if(c=='^') digit.push(pow(b,a));
}
int main(){
string str;
cin>>str;
int len=str.length();
int x=0; bool tag=false;
for(int i=0;i='0'&&str[i]<='9'){
x=x*10+str[i]-'0';
tag=true;
}else{
if(tag){
digit.push(x);
x=0;
tag=false;
}
if(str[i]=='('){
symbol.push(str[i]);
continue;
}
if(str[i]==')'){
while(symbol.top()!='('){
cal();
}
symbol.pop();
continue;
}
while(!symbol.empty()&&level(symbol.top())>=level(str[i])){
cal();
}symbol.push(str[i]);
}
}
if(tag){
digit.push(x);
}
while(!symbol.empty()){
cal();
}
cout << digit.top() << endl;
return 0;
} 五、信息学oj-1357:车厢调度(train)
(1)问题描述
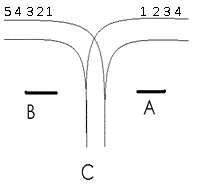
有一个火车站,铁路如图所示,每辆火车从A驶入,再从B方向驶出,同时它的车厢可以重新组合。假设从A方向驶来的火车有nn节(n≤1000n≤1000),分别按照顺序编号为11,22,33,…,nn。假定在进入车站前,每节车厢之间都不是连着的,并且它们可以自行移动到B处的铁轨上。另外假定车站C可以停放任意多节车厢。但是一旦进入车站C,它就不能再回到A方向的铁轨上了,并且一旦当它进入B方向的铁轨,它就不能再回到车站C。
负责车厢调度的工作人员需要知道能否使它以a1a1,a2a2,…,anan的顺序从B方向驶出,请来判断能否得到指定的车厢顺序。
【输入】
第一行为一个整数nn,其中n≤1000n≤1000,表示有nn节车厢,第二行为nn个数字,表示指定的车厢顺序。
【输出】
如果可以得到指定的车厢顺序,则输出一个字符串“YES”,否则输出“NO”(注意要大写,不包含引号)。
【输入样例】
5
5 4 3 2 1
【输出样例】
YES
(2)问题分析
这道题看着挺吓人,其实并没有那么难,主要就是让你确认一下出栈顺序是否正确,如果正确,则输出YES。比如,输入一个数字5,紧接着输入五个数,创建一个整形变量从1开始,因为入栈与弹栈输出的顺序正好相反,所以可以考虑输入的数比第一个小,入栈并自增,一直加到不大于这个数位置,最后如果这个数与栈顶是否相等,相等则弹出,不相等则输出NO,最后如果栈空,则输出YES
(3)代码实现
#include
using namespace std;
int main(){
stacka;
int s[1005];
int n;
cin>>n;
for(int i = 1;i<=n;i++){
cin>>s[i];
}
for(int i = 1,b = 1;i<=n;i++){
while(b<=s[i]){
a.push(b++);
}
if(a.top() == s[i]){
a.pop();
}else{
cout<<"NO";
return 0;
}
}
cout<<"YES";
return 0;
}