【追求卓越13】算法--深度和广度优先算法

引导

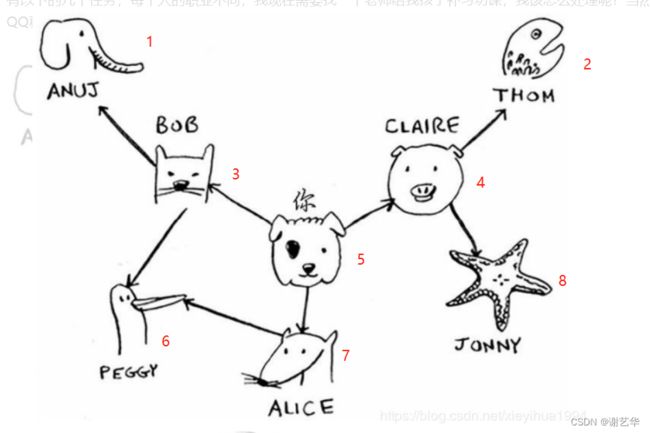
        前面的几个章节，我们介绍了树这种数据结构，二叉搜索树在进行查找方面比较高效；有二叉树演变来的堆数据结构在处理优先级队列，top K，中位数等问题比较优秀；今天我们继续介绍新的数据结构——图。它在解决多对多的问题上占有优势，比如：存储微信，微博等用户之间的好友，粉丝关系。

图的相关概念

结合图来介绍：

顶点：在树结构中，每个元素我们称为节点，图数据结构中我们称为顶点。比如，图中的A，B，C，D，E,F六个顶点

边：图中的一个节点可以和任意其他节点建立关系，我们称这个关系为边。比如图中A->C,就是一个边。

度:描述的是一个顶点相连边的个数。比如A顶点的度是3
上图是无向图，实际中我们一般处理的是有向图。

在有向图中，度分为入度和出度。

入度：表示多少个边指向该顶点。比如，A顶点的入度是1.

出度：表示多少个边是以这个顶点为起点指向其它顶点。比如，A顶点的出度是2.
在QQ中我们还有并表示用户之间的亲密度的功能，这个我们可以使用带权图来表示。

每个边上带有权重，表示亲密度。比如A有两个好友B和C，与C的亲密度要高。

如何表示图

        图的基本概念我们已经介绍完了，代码中我们如何表示图呢？图的表示方法有两种，分别是邻接矩阵和邻接表。
邻接矩阵底层依赖二维数组进行存储。如果有N个顶点，就建立Array[N][N]的二维数组。表示方式：
        如果是无向图，如果顶点i和顶点j之间有边，我们就将Array[i][j]和Array[j][i]置为1；对于有向图，如果顶点i到顶点j之间，有一条从i指向j的边，我们就将Array[i][j]置为1；对于带权图，和有向图类似，不过值不再是1，而是权重。
        因此，对于实际问题，我们需要先将用户存储到数组中，保存每个用户的下标。
邻接矩阵虽然简单，但比较浪费空间。

1. 对于无向图，实际上我们只需要将Array[i][j]置为1即可，不需要置为Array[j][i]。实际我们只需矩阵的右上半部即可。
2. 如果我们存储的是稀疏图（边的个数少），其实很也是很浪费资源的。

        但是对于用户量不是很大的情况下，我们使用邻接矩阵还是比较好的。
邻接表其实和散列表相似，依赖于指针数组存储。有N个用户，就创建Array[N]的数组大小。数组里存储的是顶点指向的顶点。
如图：

当然随着数据的变多，链表长度肯定会变长，我们可以使用哈希，或搜索二叉树来加快搜索。

广度优先算法

        数据结构是服务于算法的，广度优先算法就非常适合使用图来实现。广度优先算法（Breadth-First-Search）,我们平常简称为BFS。
        BFS一般是用于解决两样东西之间最短距离的问题；这个最短距离可以是导航中，最快到达目的地的路径顺序；也可以是象棋中，至少需要多少步取得胜利的方式；根据人脉关系，如何找到关系最近的医生。

        之前我学习算法图解的时候，我写过一个广度优先算法的程序，只不过当时并没有说明图的概念，完全用数组来实现广度优先算法-CSDN博客。现在结合图来理解，其实用到了邻接矩阵实现。并且现在对BFS又有了更加深入的理解。

思路：

1. 建立邻接表，保存每个用户之间的关系。
2. 从起始点，开始遍历，遍历完所有的相邻节点之后，再从相邻节点遍历。直至达到目标节点。

其实，这就是一个按层搜索的暴力解决方式。代码如下(没有运行验证，但思路应该如此,我会尽量说明详细);

/* 有图可知，该图是一个无向图 */ / *用于描述顶点信息* / typedef struct node {     int data;     Node* next; }Node; / *邻接表* / #deifne MAX 16 Node * peoples[MAX] = {0}; / *表示建立a顶点和b顶点之间的关系* / int create_adjtable(int a , int b) {     Node * temp = &peoples[a];     Node * peoples = NULL;     while(temp!= NULL && temp->next != NULL)     {         temp = temp->next;     }     Node * people = (Node*) malloc(sizeof(Node));     people->data = b;     people->next = NULL;     if(temp == NULL)         temp = people;     else         temp->next = people;     / *一条边是双向的* /       temp = &peoples[b];     while(temp!= NULL && temp->next != NULL)     {         temp = temp->next;     }     Node * people = (Node*) malloc(sizeof(Node));     people->data = a;     people->next = NULL;     if(temp == NULL)         temp = people;     else         temp->next = people; } / *表示求start顶点到end顶点的最短距离* / int BFS(int start ， int end) {     if(start == end) return 0; / *用于记录已经访问的节点* /     int visit[MAX] ={0};     / *用于记录到达该顶点的上一个顶底，比如2->3,我们就记录prev[3]=2,表示是从2顶点到达3顶点* /     int prev[MAX] = {0};     visit[start] = 1; / *queue表示已经访问顶点的相邻顶点,至于queue的长度为什么为MAX就可以了？* /     int queue[MAX] = {0};     int index = 0;     queue[index]=start;     int i = 0;     /**/     while(queue[i] != 0)     {         Node * temp = peoples[queue[i]];         while(temp->next != NULL)         {             / *表示该顶点没有访问* /             if(visit[temp->data] == 0)             {                 / *temp->data顶点是由queue[i]顶点过来的* /                 preve[temp->data] = queue[i];                 if(temp->data == end)                 {                     print(prev,start,end);                     return 0;                 }                 queue[++index] = temp->data;                 visit[temp->data]=1;             }             / *对于访问过的顶点，我们不再处理，因为广度优先算法是按层搜索的，即使遇到访问过的顶点，那一定不是最短路径，故可以忽略* /             temp = temp->next;         } i++;     } retunr -1; } /*递归打印*/ int print(int prev,int start,int end) {     if(end != start)         print(prev,start,prev[end])     printf("%d->",end); }

该代码还没有调试，但思路大致如此，如有问题还请见谅。

时间复杂度和空间复杂度

        假设图的顶点个数是V，边的个数是E。从代码的实现可知，空间复杂度不会大于O(V),毕竟start到end并不一定会遍历所有顶点。
        空间上的消耗主要是queue，prev,visit三个数组，但它们的长度不会多于V，故空间复杂度是O(V)

深度优先算法

        深度优先算法(Depth-First-Search),简称DFS。常用于走迷宫。还记得刚毕业时，我就遇到这样的面试题，结果是惨败。
        DFS和BFS相似，但实现逻辑不太一样。BFS是按层搜索找到最短路径。而DFS是按照深度搜索，他找到的路径可能不是最短路径。
如图：

不同的算法结果是不同的：

BFS算法结果:A,B,C,D,E,F,G,H

DFS算法结果:A,B,D,E,C,F,G,H
代码实现：

int dfs(int start,int end) {     int visit[MAX] = {0};     int prev[MAX] = {0};     recurdfs(visit,prev,start,end);     print(rev,start,end);     return 0; } void recurdfs(int visit[],int prev[],int start,int end) {     visit[start] = 1;     if(start == end)         return;     Node * temp = peoples[start];     while(temp->next != NULL)     {         if(visit[temp->data] == 0)         {             prev[temp->data] = start;             recurdfs(visit,prev,temp->data,end);         }         temp = temp->next;     } }

总结

        本章内容较多，我们介绍了图这种数据结构，并且介绍了图的两种算法：BFS和DFS。这两种算法的思想和逻辑需要我们反序去理解和推敲