数据结构—树与二叉树(Part Ⅶ)—并查集

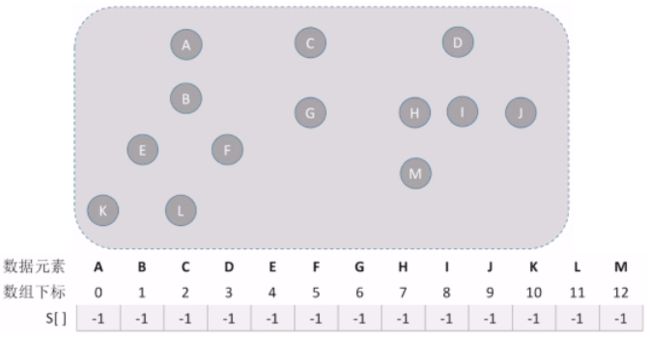
并查集的基本概念

• 并查集支持查找一个元素所属的集合以及两个元素各自所属的集合的合并等运算。当给出两个元素的一个无序对(a,b)时，需要快速“合并”a和b分别所在的集合，这期间需要反复“查找”某元素所在的集合，“并”、“查”和“集”3个字由此而来。在这种数据类型中，n个不同的元素被分为若干组，每组是一个集合，这种集合叫分离集合，称之为并查集(disjoint-set)。
• 对于给定的编号为1~n的n个元素，x表示其中的一个元素，设并查集为S，并查集的实现需要支持如下运算：

1. MAKE_SET(S，m)：初始化并查集S，即$S=S1，S2，\dots ，Sn$，每个动态集合$S_i(1\le i\le n)$仅仅包含一个编号为i的元素，该元素作为集合$S_i$的“代表”。
2. FIND_SET(S，x)：返回并查集S中x元素所在集合的代表。
3. UNION(S，x，y)：在并查集S中将x和y两个元素所在的动态集合(例如$S_x$和$S_y$合并为一个新的集合$S_x\cup S_y$。并且假设在此运算前这两个动态集合是分离的，通常以$S_x$或者$S_y$的代表作为新集合的代表。

并查集的算法实现

• 并查集必须借助某种数据结构来实现，数据结构的选择是一个重要的环节，选择不同的数据结构可能会在查找和合并的操作效率上有很大的差别。并查集的数据结构的实现方法很多，使用比较多的有数组实现、链表实现和树实现。这里主要介绍树实现方法，树的存储结构主要有三种：双亲存储结构、孩子链存储结构以及孩子兄弟存储结构。对于并查集的操作而言，需要快速找到一个结点的双亲结点，因此适用双亲存储结构是最合适不过的。
  
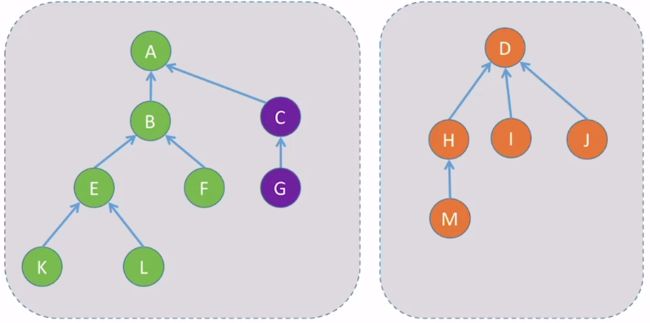
• 用有根树表示集合，树中的每个结点包含集合的一个元素，每棵树表示一个集合。多个集合形成一个森林，以每棵树的树根作为集合的代表，树中每个结点有一个指向双亲结点的指针，根结点的双亲结点指针指向其自身。
• ！注意：在同一棵树中的结点属于同一个集合，虽然它们在树中存在父子结点关系，但并不意味着它们之间存在从属关系。树中的指针起的只是联系集合中元素的作用在并查集中，每个分离集合对应的一棵树称为分离集合树。整个并查集也就是一个分离集合森林。
  
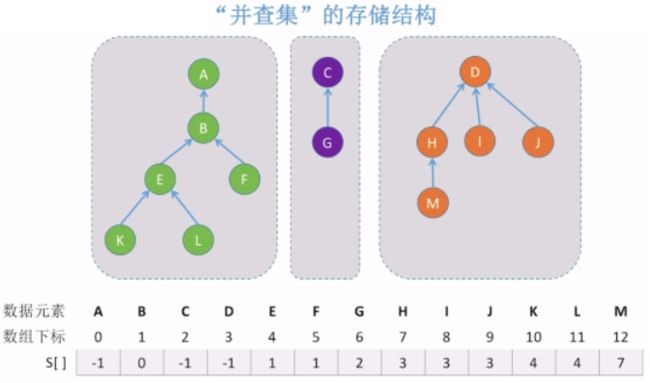
• 为了方便，采用顺序方法存储森林，其结点的类型声明如下：

#define SIZE 100
int UFSets[SIZE]; //集合元素数组(双亲指针数组)

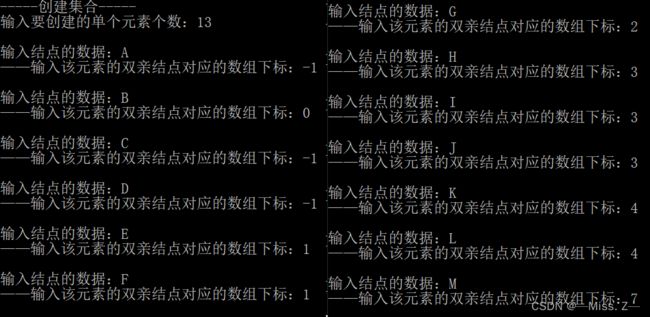
并查集树的初始化

• 建立一个存放并查集树的数组t。

void Initial(int S[]) //初始化
{
	for (int i = 0; i < SIZE; i++)
		S[i] = -1; //每个自成单元素集合
}

查找一个元素所属的集合

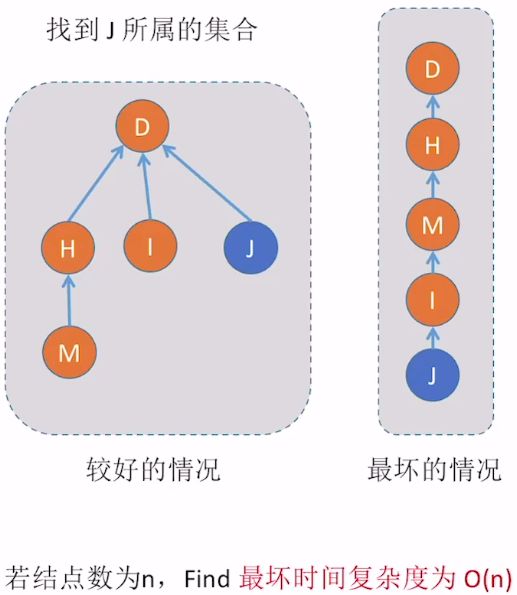
• 在分离集合森林中，每一棵分离集合树对应一个集合。如果要查找某一元素所属的集合，就是要找这个元素对应的结点所在的分离集合树。
• 不妨以分离集合树的根结点的编号来标识这个分离集合树，这样查找一个结点所在的分离集合树也就是查找该结点所在分离集合树的根结点。
• 查找树的根结点的方法很简单，只需任取树中的一个结点(不妨取要查找的那个结点)，沿双亲结点方向一直往树根走：初始时，取一个结点，走到它的双亲结点，然后以双亲结点为基点，走到双亲结点的双亲结点，…，直至走到一个没有双亲结点的结点为止，这个结点就是树的根结点。

int Find(int S[], int x) //在并查集S中查找并返回包含元素x的树的根
{
	while (S[x] >= 0) x = S[x]; //循环寻找x的根
	return x; //根的S[ ]<0
}

• 对于n个结点，查找一个元素所在的集合最好的时间复杂度为O(1)，最坏的时间复杂度为O(n)。
  

两个元素各自所属的集合的合并

• 给定两个元素，首先要找到它们各自所属的集合，如果二者已属于同一个集合，则不需要进行任何操作，如果二者所属不同的集合(二者所在树的根结点不同)，才有进行合并的必要。

void Union(int S[], int x, int y) //求两个不相交子集合的并集
{
	int Root1 = Find(S, x);
	int Root2 = Find(S, y);
	if (Root1 == Root2) return; //要求Root1和Root2是不同的，且表示子集合的名字
	S[Root2] = Root1; //将根Root2连接到另一根Root1下面
}

• 合并两个集合的元素首先要分别找到二者所在的树的根，因此时间复杂度与查找相同，找到两个根结点再进行合并只需要O(1)的时间复杂度。

并查集的优化

• 显然在一棵高度较低的树中查找根结点的编号(即该集合的代表)所花的时间较少。因此，并查集的优化主要是想办法让树变得"矮胖"，从而提高查找的效率。

合并时调整

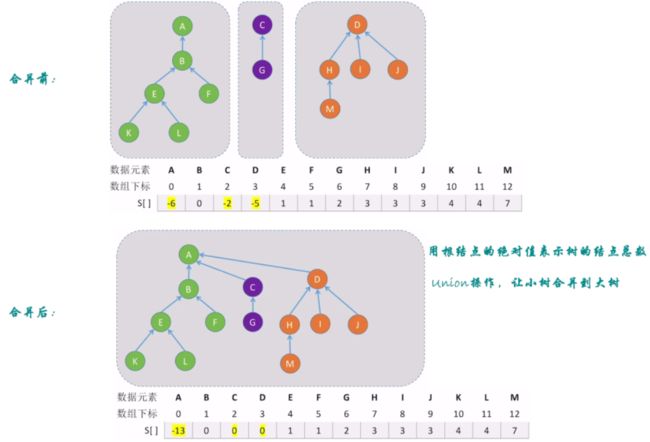
• 如果有两棵分离集合树A和B，高度分别为$h_A$和$h_B$，若$h_A>h_B$，应将B树作为A树的子树；否则，应将A树作为B树的子树。总之，总是将高度较小的分离集合树作为子树。得到了新的分离集合树C的高度$h_c$，如以B树作为A树的子树，$h_c=MAX\{h_A，h_B+1\}$。
  

void Union1(int S[], int x, int y) //并集优化
{
	int Root1 = Find(S, x);
	int Root2 = Find(S, y);
	if (Root1 == Root2) return; //要求Root1和Root2是不同的，且表示子集合的名字
	if (S[Root2] > S[Root1]) //Root2结点数更少
	{
		S[Root1] += S[Root2]; //累加结点总数
		S[Root2] = Root1; //小树合并到大树
	}
	else
	{
		S[Root2] += S[Root1]; //累加结点总数
		S[Root1] = Root2; //小树合并到大树
	}
}

• 这样合并得到的分离集合树的高度不会超过$lo{g}_2^n$，是一个比较平衡的树，对应的查找与合并的时间复杂度也就稳定在$O(lo{g}_2^n)$了。

进行路径压缩

• 除了在集合合并时调整之外，路径压缩也是一种良好的方案。它是指：将某个要查找的结点到根结点路径上所有的结点直接连接到根结点的下方。这样做的好处是，在下次要查找该结点时，时间复杂度仅需要O(1)。

int Find1(int S[], int x) //路径压缩
{
	int root = x;
	while (S[root] >= 0) root = S[root]; //循环找到根
	while (x != root) //压缩路径
	{
		int t = S[x]; //t指向x的父结点
		S[x] = root; //x直接挂到根结点下
		x = t;
	}
	return root; //返回根结点编号
}

• 每次Find操作，先找根，再"压缩路径"，可使树的高度不超过$O(\alpha (n))$。$\alpha (n)$是 一个增长很缓慢的函数，对于常见的n值，通常$\alpha (n)$<4，因此优化后并查集的Find、Union操作时间开销都很低。

并查集的应用

判断图的连通分量数 & 判断图是否有环

• 判断图(有向图/无向图)的连通分量数：初始时，将每个顶点看成是单独的集合，遍历邻接矩阵(或邻接表)，当发现两个顶点之间存在路径时，将这两个顶点合并到一个集合中。当遍历结束后，统计并查集数组中双亲指针域里有几个负数，该值就是图的连通分量数。

• 判断图(只能是无向图)是否有环：在判断图的连通分量数的功能上，增加一个判断：如果遍历到两个顶点时，发现在此前的遍历中已经将这两个顶点合并到了一个集合，则说明此时图中必然存在环。

代码实现

利用并查集判断图是否有环以及图中连通分量的个数

Kruskal算法

• 此应用的代码实现要稍微复杂一点，主要是需要将各条边按照权值进行排序，之后的操作与实现"判断图的连通分量数 & 判断图是否有环"类似。
• Kruskal算法的基本原理及相关代码
  

总结

完整代码

#include
#include
#define SIZE 50  //定义数组最大容量
typedef char ElemType; //结点数据类型定义为字符型
typedef struct
{
	ElemType data; //数据域
	int parent; //双亲结点域
}UFSets[SIZE]; //并查集类型

void Initial(UFSets S[]) //初始化
{
	for (int i = 0; i < SIZE; i++)
	{
		S[i]->data = -999; //初始时不设结点值
		S[i]->parent = -1; //每个自成单个元素集合，初始时父结点全部设为-1
	}
}

void Create(UFSets S[], int i) //创建数组表信息
{
	ElemType data; //结点数据域为字符型
	int parent; //结点双亲域为整型
	printf("\n输入结点的数据：");
	getchar(); //获取数据域信息
	scanf("%c", &data);
	S[i]->data = data; //存数据信息
	printf("——输入该元素的双亲结点对应的数组下标：");
	scanf("%d", &parent);
	S[i]->parent = parent; //双亲结点信息
}

void AdjustArrTable(UFSets S[], int num)
//调整数组双亲结点信息，用根结点的绝对值代表集合中元素的个数
{
	for (int i = 0; i < num; i++)
	{
		int j = i;
		while (S[j]->parent >= 0)
		{
			j = S[j]->parent; //不断向上找到根结点
			if (S[j]->parent < 0) S[j]->parent -= 1;
			//当该集合中每增加一个元素时，根结点的双亲信息值-1，取绝对值，表示当前集合中元素的个数
		}
	}
}

/*int Find(UFSets S[], ElemType x, int num) //在并查集S中查找并返回包含元素x的树的根的数组下标
{
	int i = 0;
	while (S[i]->data != x ) i++; //这里传入的是数据结点信息，不是数组下标，因此需要遍历一次
	if (i >= num) return -999; //不存在值为x的数据结点
	while (S[i]->parent >= 0) i = S[i]->parent; //通过双亲结点不断向上找树的根
	return i; //返回根结点信息
}*/

/*bool Union(UFSets S[], char x, char y, int num) //求两个不相交子集合的并集
{
	int Root1 = Find(S, x, num); //查找子集x的根结点
	int Root2 = Find(S, y, num);; //查找子集y的根结点
	if (Root1 == Root2) return false; //根结点相同则不进行合并
	else
	{
		S[Root1]->parent += S[Root2]->parent; //集合中总结点数增加
		S[Root2]->parent = Root1;
		return true;
	}
}*/

int Find1(UFSets S[], ElemType x, int num) //Find优化(即路径压缩)
{
	int i = 0, j;
	while (S[i]->data != x) i++; //这里传入的是数据结点信息，不是数组下标，因此需要遍历一次
	if (i >= num) return -999; //不存在值为x的数据结点
	j = i;
	while (S[j]->parent >= 0) j = S[j]->parent; //通过双亲结点不断向上找树的根
	while (S[i]->parent >= 0)
	{
		int t = S[i]->parent;
		S[i]->parent = j;
		i = t;
	}
	return j; //返回根结点信息
}

bool Union1(UFSets S[], ElemType x, ElemType y, int num) //Union优化(即将小集合并入大集合中)
{
	int Root1 = Find1(S, x, num); //查找子集x的根结点
	int Root2 = Find1(S, y, num);; //查找子集y的根结点
	if (Root1 == Root2) return false; //根结点相同则不进行合并
	if (abs(S[Root1]->parent) > abs(S[Root2]->parent))
	{
		S[Root1]->parent += S[Root2]->parent; //集合中总结点数增加
		S[Root2]->parent = Root1;
	}
	else
	{
		S[Root2]->parent += S[Root1]->parent; //集合中总结点数增加
		S[Root1]->parent = Root2;
	}
	return true;
}

void Print(UFSets S[], int num) //打印数组中结点的信息
{
	for (int i = 0; i < num; i++)
		printf("\n%c(%d)", S[i]->data, S[i]->parent); //打印数据信息以及双亲结点信息
}

int main()
{
	UFSets S[SIZE];
	int num;
	Initial(S);
	printf("-----创建集合-----");

	printf("\n输入要创建的单个元素个数：");
	scanf("%d", &num);
	for (int i = 0; i < num; i++) Create(S, i);

	AdjustArrTable(S, num);
	printf("\n-----打印信息表-----");
	Print(S, num);

	ElemType data;
	printf("\n\n-----在并查集S中查找并返回包含元素x的树的根-----");
	printf("\n输入要查找的元素的数据：");
	data = getchar();
	scanf("%c", &data);
	int i = Find1(S, data, num);
	printf("包含元素%c的树的根的数据为：%c", data, S[i]->data);
	
	printf("\n-----打印信息表-----");
	Print(S, num);

	ElemType x, y;
	bool result;
	printf("\n\n-----求两个不相交子集的并集-----");
	printf("\n输入两个不相交的数据元素");
	printf("\n输入第一个数据：");
	x = getchar();
	scanf("%c", &x);
	printf("输入第二个数据：");
	y = getchar();
	scanf("%c", &y);
	result = Union1(S, x, y, num);
	printf("\n合并结点%c和%c所在的两个集合——合并成功了吗？——%d(0代表失败，1代表成功)", x, y, result);
	if (result) Print(S, num);
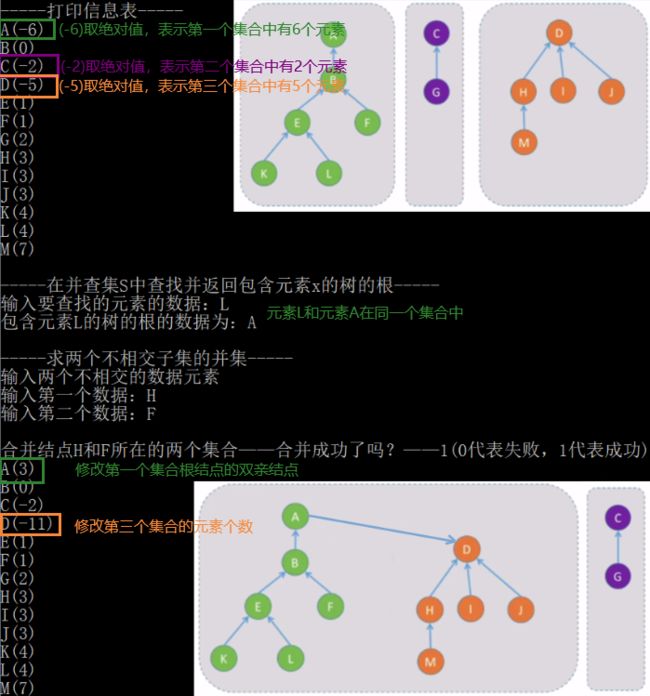
	return 0;
}

运行结果

两种优化方式的运行结果：

• Union优化(即将小集合并入大集合中)
  
• Find优化(即路径压缩)
  

---

补充：在使用scanf("%c",&data);读取一个字符时，有时会遇到scanf吞回车符的情况。 这里所搜到几种常用的解决方法：

1. 在scanf()中使用’\n’屏蔽回车符号。

scanf("\n%c",&c);

2. 在scanf()格式串最前面添加空格，屏蔽回车字符

scanf(" %c",&c); //%c前面加空格，过滤回车

3.在接收字符前，使用getchar()来读取一次回车符号

getchar(); //专门用来读取上次输入的回车符号
scanf("%c",&c);

！此次代码读取字符采取的是这种形式

4. 在接收字符前，使用fflush()清空输入流中缓冲区中的内容

fflush(stdin); //清空输入流缓冲区的字符，注意必须引入#include头文件
scanf("%c",&c);