算法笔记【并查集】

算法介绍

并查集：是一个可以动态维护若干个不重叠的集合，并支持合并与查询的数据结构。详细的说，并查集包括如下两个基本操作。

1. find：查询一个元素属于哪一个集合
2. Merge：把两个集合合并成一个大集合

为了实现并查集这种数据结构，：

1. 需要定义集合的表示方法：

在并查集中，我们采用“代表元”法，即每个集合选择一个固定的元素，作为整个集合的“代表”。

2. 需要定义归属关系的表示方法：
   第一种思路：

维护一个数组 $f$，用 $f[x]$ 保存元素 $x$ 所在集合的“代表”。
这种方法可以快速查询元素的归属集合，但在合并时需要修改大量元素的 $f$ 值，效率很低。

第二种思路：

使用一种树形结构存储每个集合，树上的每一个节点都是一个元素，树根是集合的代表元素。
整个并查集就相当一个森林（若干棵树）。我们仍然可以维护一个数组 $fa$ 来记录这个森林，用 $fa[x]$ 保存 $x$ 的父节点。特别地，令树根的 $fa$ 值为它自己。这样一来，在合并两个集合时，只需连接两个树根（令其中一个树根为另一个树根的子节点，即$fa[roo{t}_1]=roo{t}_2$)。只不过在查询元素的归属时，需要从该元素开始通过 $fa$ 储存的值不断递归访问父节点，甚至到达树根。

为了提高查询效率，并查集引用了路径压缩与按秩合并两种思想。

结构分析

路径压缩

我们可以注意到，第一种思路（直接用数组 $f$ 保存代表）的查询效率很高，我们不妨把两种思路进行结合。实际上，我们只关心每个集合对应的“树形结构”的根节点是什么，并不关心这棵树的具体形态——这意味着下面两个树是等价的：

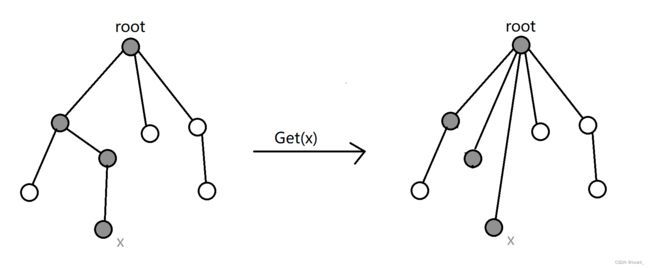
因此，我们可以在每次执行 find 操作的同时，把访问过的每个节点（也就是所谓查询元素的全部祖先）都直接指向树根，即把上图中左边那棵树变成右边那颗树。这种优化的方法就叫做路径压缩。采用路径优化的并查集，每次 Get 操作发均摊复杂度为$O(logN)$。

按秩合并

虽然路径压缩单论询问速度来说要比按秩合并快，但是它会在压缩路径的同时破坏原有的父子关系，这对某些题来说这是不可以的，那么按秩合并就要相对快些了。

我做题的时候没遇到过这样的题，这里就不多解释了。

代码实现

1. 并查集的储存：

使用一个数组$fa$保存父节点(根的父节点设为自己)

int fa[size];

2. 并查集的初始化：

设有 $n$ 个元素，起初所有元素各自构成一个独立的集合，即有 $n$ 棵 1 个点的树。

for(int i = 1; i <= n; i++) fa[i] = i;

3. 并查集的find操作

若 $x$ 是树根，则 $x$ 就是集合的代表，否则递归访问 $fa[x]$ 直至根节点。

int find(int x)
{
	if(x != fa[x]) fa[x] = find(f[x]);
	return x; 
}

例题：

1. 程序自动分析（模板题）

Acwing 程序自动分析

解题思路：

该题就是一个典型的并查集问题。
先来分析该题：
该题是给定一些相等的关系和一些不相等的关系，判断相等和不相等是否矛盾。
例如，一个问题中的约束条件为：$x1=x2，x2=x3，x3=x4，x1\ne x4$，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。
我们可以看到相等的数之间是有传递性的，那么我们就可以进行并查集的计算。
又因为我们可以不管路径上的父节点，只需要知道根节点就好了，那么我们就可以用路径压缩。
基础步骤：

1. 先将相等的数进行合并。
2. 然后再依次判断给定不相等的情况下，那两个数字是否相等，如果相等的话，就说明矛盾了。

注意看数据范围：

之间用数组进行存储，空间上一定会超时，又因为，数据的绝对大小对结果没有影响，那么我们就需要进行离散化处理。
可以直接用哈希表来实现(unordered_map)；
下面就是代码实现阶段。

STHW TIME

代码实现：

#include
#include
#include
#include
using namespace std;

struct node{
    int a,b,x;
}item[201000];
int idx = 0;
unordered_map<int,int> fa;
int father[200100];

int down(int x)
{
    if(fa.count(x)) return fa[x];
    return fa[x] = idx++;
}

int find(int x)
{
    if(father[x] != x) father[x] = find(father[x]);
    return father[x];
}

void solve()
{
    int n;
    cin >> n;
    fa.clear();
    idx = 1;
    for(int i = 1; i <= 200000; i++) father[i] = i;
    for(int i = 1; i <= n; i++)
    {
        scanf("%d%d%d",&item[i].a,&item[i].b,&item[i].x);
        item[i].a = down(item[i].a);
        item[i].b = down(item[i].b);
        if(item[i].x)
        {
            father[find(item[i].a)] = find(item[i].b);
        }
    }
    for(int i = 1; i <= n; i++)
    {
        if(item[i].x == 0)
        {
            if(find(item[i].a) == find(item[i].b))
            {
                puts("NO");
                return ;
            }
        }
    }
    puts("YES");
}

int main (void)
{
    int T;
    cin >> T;
    while(T--)
    solve();
    return 0;
}

2. 超市（模板拓展题）

Acwing 超市

解题思路：

该题本来用二叉堆来写的，用二叉堆也特别简单，但也可以用并查集来写，之前受二叉堆的影响，也没有写出来。最后看的题解理解的，该题用并查集很巧妙，时间复杂度缩短了3倍，因此用这个方法也是很不错的选择。

首先分析该题：
通过读题可以知道，需要在时间限制内尽可能装价值更大的物品，那么:

1. 我们就需要先进行升序排序，将排完序之后的所有的值从前往后进行遍历，将该物品放置在过期的当天卖出去（听起来有点像奸商的感觉）。
2. 如果遇到该天被占用的情况，那么就向前找，找到一个没有占用的天数，然后在该天卖出去。

这个是基本思路，细心的同学已经想到了，向前找一个没有被占用的天数，怎么找，总不能向前一个一个遍历吧，这时就可以介绍今天的“重要人物”并查集了。

那么怎么去实现这一操作呢：

1. 我们定义一个并查集数组，然后按照并查集的初始化方法对该数组进行初始化
2. 我们每放置一个数组的时候就先进行并查集查找，如果找到一个该坐标前面（包括它本身）的坐标有空位就坐进去，找到了就将该点的放入该天数中，然后将该点指向放入的天数的下一个天数（注意是下一个天数，不是下一个空位），然后进行下一步操作，依次类推。
3. 如果发现找到的值是小于等于0的，那么说明前面已经没有空位置能放了，那就不放。
4. 最后我们来分析一下为啥可行，因为我们每次操作都是将最大价值的那个物品放置在最后会过期的那天，这样即保证了每次卖出的价值最大，又保证了该物品不会占用别的物品的空间，这就是满足的条件。

这样分析有讲清楚吧，不清楚的话那就看代码吧，相信聪明的你一定能结合代码和分析讲这个题理解透。
我感觉这个题不仅是这一种题，而是一个类型题，所以，经历将该题理解透彻。

代码实现：

#include
#include
using namespace std;

struct node{
    int profit,time;
}item[10010];
int f[10010];
bool cmp(node x,node y)
{
    return x.profit > y.profit;
}
int find(int x)
{
    if(f[x] != x) f[x] = find(f[x]);
    return f[x];
}

int main (void)
{
    int n;
    while(cin >> n)
    {
        int maxx = 0;
        for(int i =1 ; i <= n;i++)
        {
            scanf("%d%d",&item[i].profit,&item[i].time);
            if(item[i].time > maxx) maxx = item[i].time;
        }
        sort(item+1,item+1+n,cmp);
        for(int i = 0; i <= maxx; i++) f[i] = i;
        int profits = 0;
        for(int i = 1; i <= n; i++)
        {
            int x = find(item[i].time);
            if(x > 0)
            {
                f[x] = x - 1;
                profits += item[i].profit;
            }
        }
        cout << profits << endl;
    }

    return 0;
}

学习普及：
怎么查看代码运行时间：

#include
#include
using namespace std;
int main (void)
{
	clock_t start,end;
	start = clock();
	// 此处省略代码
	end = clock();
	cout << (double)(end - start)/CLOCKS_PER_SEC << endl;
}

3. 银河英雄传说（带权并查集）

Acwing 银河英雄传说

解题思路

带权并查集
该题要仔细分析题意，不能被题意带跑偏：
它是指要将这一列的排头加在另一列的尾部。
那么我们就需要查找每一列的最前面的那个排头，然后按照路径压缩的思路将每一列都指向前面的排头，那么这样就可以求得每一个到最前面的那个间隔，那么如果要求两个数的间隔，那么就直接用两个数到前面的那个间隔相减取个绝对值就好了。

图解：

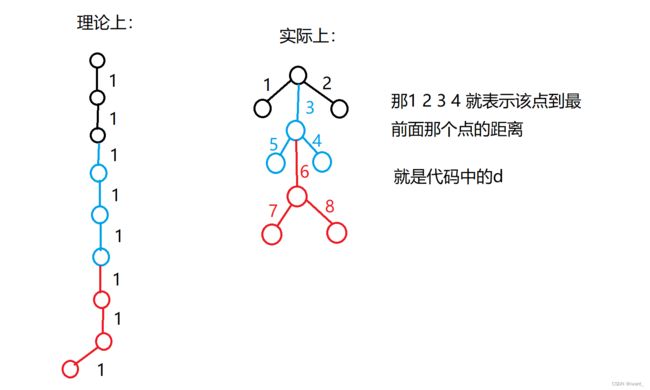
那个s就是size，表示的是该节点有多少个子节点。
这样就很好理解了吧，那么下面代码实现就请看代码吧。

代码实现：

#include
using namespace std;
int p[30005], s[30005, d[30005];
int find(int u)
{
    if(p[u] != u) {
        int t = find(p[u]);
        d[u] += d[p[u]];   // 因为我们只更新了最前面的那个值，而中间的值并未更新，那么我们就需要在遍历的时候更新
        p[u] = t;  // 注意这个语句，因为我们需要倒着进行更新数值，那么我们就需要赋值在更新的前面。
    }
    return p[u];
}

int main(void)
{
    int T;
    cin >> T;
    for(int i = 1; i <= 30000; i++) p[i] = i,s[i] = 1;
    
    for(int cases = 1; cases <= T; cases++)
    {
        char ch;
        int a,b;
        cin >> ch >> a >> b;
        int x = find(a);
        int y = find(b);
        if(ch == 'M'){
            if(x != y)
            {
                p[x] = y;     // 这个就表示将 x 接在 b 对应的最前面的那个节点的后面
                d[x] = s[y];  // 因为 x 是 a 节点的最前面的那个值，那么 d[x] 这个就表示将 a 的最前面的那个值接在b的父节点上，d[x] = s[y] 表示的的前面有s[y] 个值。 
                s[y] += s[x];
                // 这个语句就表示将 x 接在 y 的后面，那么 y 的个数就增加 x 个。
            }
        }
        else {
            if(x != y)
            cout << "-1" << "\n";
            else
            cout << max(0,abs(d[a] - d[b])-1) << "\n";
        }
    }
    
    return 0;
}

4. 奇偶游戏（边带权并查集）

Acwing 奇偶游戏

解题思路：

该题有点难理解，请细心观看
首先来分析：
对于区间内的奇数个1还是偶数个1，可以转化为区间奇偶性的判断。

1. 对于一个区间[l,r]中1的个数是奇数的时候，那么r 和 l-1 的奇偶性不同
2. 对于一个区间[l,r]中1的个数是偶数的时候，那么r 和 l-1 的奇偶性相同

又因为：

1. x1 与 x2 的奇偶性相同，x2 和 x3 的奇偶性相同，那么 x1 和 x3 的奇偶性相同
2. x1 与 x2 的奇偶性不同，x2 和 x3 的奇偶性相同，那么 x1 和 x3 的奇偶性不同
3. x1 与 x2 的奇偶性不同，x2 和 x3 的奇偶性不同，那么 x1 和 x3 的奇偶性不同

那么我们就可以使用带权并查集的思路来写。
判断思路是和第一题的思路相似
边带权的处理和第三题相似
注意看数据范围：

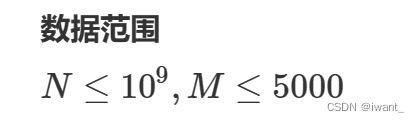
我们可以想到不能直接用数组来存储，需要进行一步离散化处理。
离散化处理我是习惯用unordered_map来进行相对应的处理。

下面就是紧张刺激的代码环节。

代码实现

#include
#include
using namespace std;
unordered_map<int,int> mp;
int v = 0;

int f[5005];
int w[5005];

int find(int x)
{
    if(f[x] != x) {
        int t = find(f[x]);  
        w[x] ^= w[f[x]]; // 该语句上一题已经分析过了，不懂的再回去看看。
        f[x] = t;
    }
    return f[x];
}

int main (void)
{
    int n,m;
    cin >> m >> n;
    for(int i = 0; i <= 5005; i++) f[i] = i;
    m = 0;
    int res = n;
    
    for(int i = 1; i <= n; i++)
    {
        int a,b;
        string ch;
        cin >> a >> b >> ch;
        int t1,t2;
        // 离散化处理
        //--------------------------------------
        if(!mp.count(a-1))mp[a-1] = ++v,t1 = v;  // 因为我们要找一个数前面的那个值，所以这里的a需要减一
        else t1 = mp[a-1];
        if(!mp.count(b))mp[b] = ++v,t2 = v;
        else t2 = mp[b];
        //--------------------------------------
        int x = find(t1),y = find(t2);
        int t = 0;
        if(ch == "odd") t = 1;
        if(x != y)
        {
            f[x] = y;
            w[x] = w[t1] ^ w[t2] ^ t;
        }
        else
        {
            if((w[t1] ^ w[t2]) != t)    // 这里就是判断奇偶性，用位运算的方法进行计算。
            {
                res = i-1;
                break;
            }
        }
    }
    cout << res << endl;
    return 0;
}

5. 食物链（带权并查集）

Acwing 食物链

解题思路

关系传递的本质实际上是向量的运算
该题要仔细审题，把题读懂（我就刚开始没读懂题）
该题讲食物链中存在一种特殊的关系，比如有三种动物， A，B，C。

• A吃B，B吃C，那么C和A就是同类

所以该题就需要用到带权并查集来判断两个动物之间是不是同类。

1. 如果相等的话，就判断与题意是否一致：
2. 如果不相等的话就进行插入，注意插入的数值，我们将同类和敌对关系混在了一起，所以，要在插入的时候进行特殊处理

具体实现请看代码。

代码实现：

#include
using namespace std;

int f[50005];
int d[50005];
int find(int x)
{					
    if(x != f[x]) {
        int t = find(f[x]);
        d[x] += d[f[x]];       
      f[x] = t;
    }
    return f[x];
}

int main (void)
{
    int n,k;
    cin >> n >> k;
    for(int i = 0; i <= n; i++) f[i] = i;
    int res = 0;
    for(int i = 1; i <= k; i++)
    {
        int op,a,b;
        cin >> op >> a >> b;
        if(a > n || b > n || (a == b && op == 2))
        {
            res ++;
            continue;
        }
        int cur;
        if(op == 2) cur = 1;
        else cur = 0;
        int x = find(a),y = find(b);
        if(x == y)
        {
            if((((d[a] - d[b]) % 3) + 3)%3 != cur) // 多加的+3和%3是为了处理负数的情况
            //0代表ab是同类，1代表a吃b，2代表a被b吃。直接与cur进行比较即可
                res ++;
        }
        else {
            f[x] = y;
            d[x] = d[b] - (d[a] - cur);
            // 如果是a吃b的话路径就存1，否则就存0
        }
    }
    cout << res << endl;

    return 0;
}