239. 奇偶游戏 —— 并查集带权 & 扩展域

题面

AcWing239

带权并查集

每次输入会告诉我们区间$[L,R]$有奇数个一或者偶数个一；

如果我们将数组$S$看成是前缀和数组；

那么相当于每次告诉我们$S(R)-S(L-1)$的结果是奇数还是偶数；

如果结果是奇数，那么说明$S(R)和S(L-1)$的奇偶性是不同的；

如果结果是偶数，那么说明$S(R)和S(L-1)$的奇偶性是相同的；

---

现在我们将奇数分为一类，将偶数分为另一类；

题目转化成这样；

每次告诉我们两个数之间的关系，要我们判断什么时候出现矛盾；

---

我们用$0$来代替偶数类，$1$来代替奇数类(等价类的概念，离散数学了解一下)；

设$x,y$是每次给定的两个数；

$px,py$是$x,y$的父亲节点；

$d(i)$表示点$i$与其父亲的关系，为0说明与父节点同类，为1说明与父节点异类；

---

一、当$x,y$是同类时

若有$px=py$；

$d(x)\oplus d(y)=0$ 说明没问题；
$d(x)\oplus d(y)=1$ 说明矛盾了；

注意，这里的$d(x),d(y)$他们都是路径压缩到同一个根上的结果，下同；

若有$px\ne py$；

那么我们需要合并，怎么合并呢？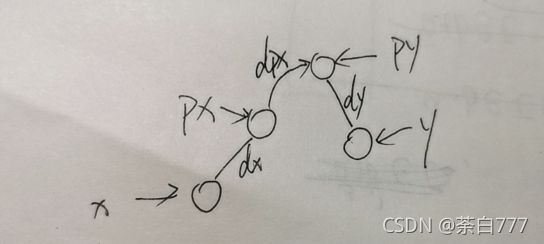
假定我们是将$x$的集合合并到$y$的集合中；

我们只需要求出图中的$d(px)$，然后令$p(px)=py$即可；

$x$到根节点(图中的$py$)的路径可以表示为$d(x)+d(px)$

注意这里的路径是表示关系的；

根据含义，$x$与$y$是同类;

则有$d(x)\oplus d(y)\oplus d(px)=偶数=0$

即$d(px)=d(x)\oplus d(y)\oplus 0$

当$x,y$是异类时

同理我们可以分析;

若有$px=py$；

$d(x)\oplus d(y)=1$ 说明没问题；
$d(x)\oplus d(y)=0$ 说明矛盾了；

---

若有$px\ne py$；

根据含义，$x$与$y$是异类;

可以推出$d(x)\oplus d(y)\oplus d(px)=奇数=1$

则$d(px)=d(x)\oplus d(y)\oplus 1$

总结

---

Code

代码中的param是为了代码的复用性，结合上面的公式，很容易理解；

#include 
#include 
#include 

using namespace std;

const int N = 2e4 + 10;

unordered_map<int,int> S;

//d(i)是当前节点与其父亲节点的关系
//为0说明同类,为1说明异类
int n,m,d[N],p[N];

int get(int x){
    if(!S.count(x)) S[x] = ++n;
    return S[x];
}
void init(){
    for(int i=1;i<N;++i){
        p[i] = i;
        d[i] = 0;
    }
}
int _find(int x){
    if(x != p[x]){
        int root = _find(p[x]);
        //路径压缩
        //合并到根上，先走自己到父亲，再走父亲到根
        //我们只需要维护两种关系 因此mod 2
        d[x] = (d[x]+d[p[x]])%2;
        p[x] = root;
    }
    return p[x];
}
int main(){
    init();
    cin >> n >> m;
    //n没用,直接hash掉
    n = 0;
    int L,R;
    string op;
    int ans = m;
    for(int i=1;i<=m;++i){
        cin >> L >> R >> op;
        //转化为S(R)与S(L-1)的关系
        L = get(L-1);
        R = get(R);
        int param = 0;
        if(op == "odd"){
            param = 1;
        }
        int pL = _find(L),pR = _find(R);
        if(pL == pR){
            if((d[L]^d[R]^param) == 1){
                ans = i-1;
                break;
            }
        }else{
            //merge
            d[pL] = d[L] ^ d[R] ^ param;
            p[pL] = pR;
        }
    }
    cout << ans << '\n';
    return 0;
}

扩展域

和我们上面提到的一样，也是先用前缀和思想分类；

如果结果是奇数，那么说明$S(R)和S(L-1)$是异类；

如果结果是偶数，那么说明$S(R)和S(L-1)$性是同类；

---

我们规定，如果$x$是奇数，那么$x+B$是偶数；

如果$x$是偶数，那么$x+B$是奇数；

---

当$x$和$y$是同类时，我们可以推出$x+B$和$y+B$是同类；

当$x$和$y$是异类时，我们可以推出$x+B$和$y$是同类以及$x$与$y+B$是同类；

注意：这里的$x$不再简单的代表一个元素，我们将其分为两个条件($x$和$x+B$)；

那么我们判断矛盾就很简单了；

比如$x,y$同类，我们只需要判断$x$与$y+B$是否是同类(或者$y$与$x+B$是否是同类)，如果是，则说明矛盾；

---

也就是说，这里我们维护了两个集合；

其中一个集合维护一些数是偶数的条件

另一个集合维护一些数是奇数的条件

Code

#include 
#include 

using namespace std;

const int N = 4e4+10;//一共2e4个点,每个点又分裂成2个点来表示

const int B = N/2;

int p[N],n,m;

unordered_map<int,int> S;

int get(int x){
    if(!S.count(x)) S[x] = ++n;
    return S[x];
}

void init(){
    for(int i=1;i<N;++i) p[i] = i;
}
int _find(int x){
    if(x == p[x]) return x;
    return p[x] = _find(p[x]);
}
int main(){
    init();
    cin >> n >> m;
    n=0;
    int ans = m;
    for(int i=1;i<=m;++i){
        int L,R;
        string type;
        cin >> L >> R >> type;
        L = get(L-1),R=get(R);
        if(type == "even"){
            //判断一对即可，另一对是对称的
            if(_find(L+B) == _find(R)){
                ans = i-1;
                break;
            }
            p[_find(L)] = _find(R);
            p[_find(L+B)] = _find(R+B);
        }else{
            if(_find(L) == _find(R)){
                ans = i-1;
                break;
            }
            p[_find(L)] = _find(R+B);
            p[_find(L+B)] = _find(R);
        }
    }
    cout << ans << '\n';
    return 0;
}

带权与扩展域区别？

带权并查集的复杂度和分类的数量无关，而扩展域是有关的。

所以当类别很多时，只能用带权并查集。

---

带权并查集往往是维护一种相对的关系；

并且在同一个集合中的都是有关系的，但是具体关系要取决于我们的取值(比如上面提到的同类、异类，都是属于有关系的)；

---

扩展域里面维护的是一组条件；

在同一个集合中的条件，只要其中一个满足了，那么其他的条件也必须满足；

而扩展域并查集中的元素也不是一个简单的元素了，而是分裂成若干个(取决于多少类)条件；