【算法】学习笔记(二)----快速排序的深入理解
快速排序的深入理解:
学习自视频:6-1 快速排序的基本思想_哔哩哔哩_bilibili
算法验证:912. 排序数组 - 力扣(LeetCode)
快速排序思想
减而治之:逐渐缩小解决问题的规模
认识快速排序的路径
采用随机划分的优点:
- 避免原数组接近于有序而导致的递归树倾斜,使用随机划分可以一定程度上避免递归树倾斜
partition法:
class Solution {
public:
vector sortArray(vector& nums)
{
srand(time(0));
quciksort(nums, 0, nums.size() - 1);
return nums;
}
void quciksort(vector& nums, int left, int right)
{
if (left >= right) return;
int index = rand() % (right - left + 1) + left;
swap(nums[left], nums[index]);
int piovtindex = partition(nums, left, right);
quciksort(nums, left, piovtindex - 1);
quciksort(nums, piovtindex + 1, right);
}
int partition(vector& nums, int left, int right)
{
int pivot = nums[left], j = left;
//划分成一下两个区间
//左边区间 nums[left + 1 ... j] <= pivot
//右边区间 nums(j ... i) > pivot
//这里左边区间j初始化为j = left表示为空区间,右边区间 i 初始化为left + 1,此时右边区间也是空区间
for (int i = left + 1; i <= right; i++)
{
if (nums[i] <= pivot)
swap(nums[++j], nums[i]);
}
swap(nums[left], nums[j]);
return j;
}
};
注意:以上代码过不了全是一样数字的样例。
特殊情况:数组中有很多元素值相同,partition前交换元素可能交换前后没有区别,使用随机划分也不能很好的处理
由此产生了以下两种快速排序:
双路快速排序:
代码示例:
class Solution {
public:
vector sortArray(vector& nums)
{
srand(time(0));
quciksort(nums, 0, nums.size() - 1);
return nums;
}
void quciksort(vector& nums, int left, int right)
{
if (left >= right) return;
int index = rand() % (right - left + 1) + left;
swap(nums[left], nums[index]);
int piovtindex = partition(nums, left, right);
quciksort(nums, left, piovtindex - 1);
quciksort(nums, piovtindex + 1, right);
}
int partition(vector& nums, int left, int right)
{
int pivot = nums[left];
int le = left + 1; //le:less equals
int ge = right; //ge:greater equals
//左边区间 nums[left + 1..le) <= pivot
//右边区间 nums(ge..right) >= pivot
while (true)
{
while (le <= ge && nums[le] < pivot) le++;
while (le <= ge && nums[ge] > pivot) ge--;
// le 来到了第一个大于等于 pivot 的位置
// ge 来到了第一个小于等于 pivot 的位置
if (le >= ge) break;
swap(nums[le], nums[ge]);
le++;
ge--;
}
swap(nums[left], nums[ge]);
return ge;
}
};
三路快速排序:
三路快排有计算机科学家Dijkstra发明
三路快排优点:
代码示例:
class Solution {
public:
vector sortArray(vector& nums)
{
srand(time(0));
quciksort(nums, 0, nums.size() - 1);
return nums;
}
void quciksort(vector& nums, int left, int right)
{
if (left >= right) return;
int index = rand() % (right - left + 1) + left;
swap(nums[left], nums[index]);
pair piovtindex = partition(nums, left, right);
quciksort(nums, left, piovtindex.first);
quciksort(nums, piovtindex.second, right);
}
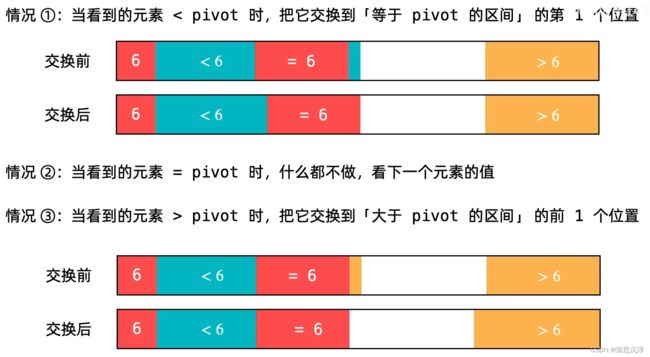
pair partition(vector& nums, int left, int right)
{
int pivot = nums[left];
int lt = left + 1; //lt:less than
int gt = right; //gt:greater than
//左边区间 nums[left + 1 .. lt) < pivot
//中间区间 nums[lt .. i) == pivot
//右边区间 nums(gt .. right) > pivot
int i = left + 1;
while (i <= gt)
{
if (nums[i] < pivot)
{
swap(nums[i++], nums[lt++]);
}
else if (nums[i] == pivot)
{
i++;
}
else if(nums[i] > pivot)
{
swap(nums[i], nums[gt--]);
}
}
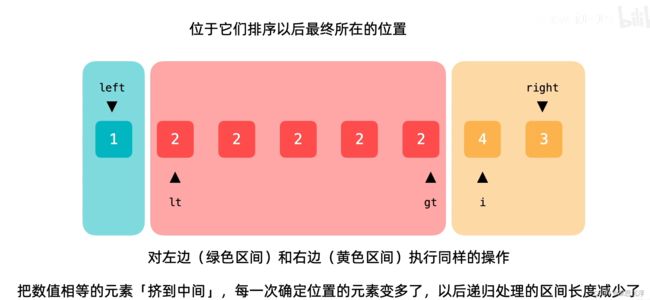
//如果存在中间的区间
//最终lt在中间区间的第一个位置,gt在中间区间的最后一个位置
//如果不存在中间的区间
//最终lt在右边区间的第一个位置,gt在左边区间的最后一个位置
swap(nums[left], nums[lt - 1]); //lt - 1是在第一个区间中,不存在第一个区间则是自己交换自己
return { lt - 2,gt + 1}; //进行上一步操作之后,此时lt位于中间区间的第二个位置所以lt - 2,如果不存在第三区间会超过数组下标,但是后面if (left >= right) return;这条语句会处理该情况
}
};