R语言时序-AR、MA与ARMA的判断及定阶
模型判断:
| ACF拖尾 | ACF截尾 | |
|---|---|---|
| PACF拖尾 | ARMA(p,q) | MA(q) |
| PACF截尾 | AR(p ) | 序列本身不存在明显的自相关性,ARMA类模型可能不适用 |
- Step1 看ACF图:
– ACF截尾:判断为MA(q)模型,q为最后一个超出2倍标准差(蓝线)的阶数,即超出水平蓝线的纵向线水量-1。
– ACF拖尾:可能为AR( p)模型也可能为ARMA(p,q)模型 - Step2 看PACF图:
– PACF截尾:AR( p)模型,p为最后一个超出2倍标准差(蓝线)的阶数,即超出水平蓝线的纵向线数量 。
– PACF拖尾:ARMA(p,q)模型,ACF和PACF看不出阶数,通过eacf定阶
【注1】传统R语言绘制的ACF图第一根竖线的阶数为零,MA(1)有两根竖线超出蓝线,但第二根的阶数不是2是1,以此类推
(1) MA
MA(1): x t = ε t + 0.4 ε t − 1 x_t = \varepsilon_t + 0.4\varepsilon_{t-1} xt=εt+0.4εt−1
MA(2): x t = ε t + 0.4 ε t − 1 − 0.7 ε t − 2 x_t = \varepsilon_t + 0.4\varepsilon_{t-1} - 0.7\varepsilon_{t-2} xt=εt+0.4εt−1−0.7εt−2
MA(3): x t = ε t + 0.4 ε t − 1 − 0.7 ε t − 2 + 0.5 ε t − 3 x_t = \varepsilon_t + 0.4\varepsilon_{t-1} - 0.7\varepsilon_{t-2} + 0.5\varepsilon_{t-3} xt=εt+0.4εt−1−0.7εt−2+0.5εt−3
ma1 <- arima.sim(n=1000, list(ma=0.4))
ma2 <- arima.sim(n=1000, list(ma=c(0.4,-0.7)))
ma3 <- arima.sim(n=1000,list(ma=c(0.4,-0.7, 0.5)))
par(mfcol=c(2,3))
ma1a <- acf(ma1)
ma1p <- pacf(ma1)
ma2a <- acf(ma2)
ma2p <- pacf(ma2)
ma3a <- acf(ma3)
ma3p <- pacf(ma3)
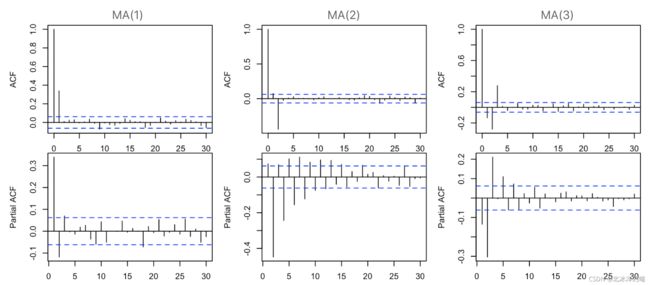
看ACF图,首先可判断上三幅ACF都是截尾,均为MA模型 。
左边ACF图第1条线对应滞后阶数为0,第2条线对应滞后阶数为1,以超出2倍标准差的最大滞后阶数作为MA模型的阶数,此时ACF超出蓝线的最大滞后阶数为1,故左边第一组应为MA(1)模型;
中间ACF图最后1条超出2被标准差水平线的纵向线阶数为2,有3条纵向线超出2倍标准差线,判断为MA(2)模型;
右边ACF图最后1条超出2被标准差水平线的纵向线阶数为3,有4条纵向线超出2倍标准差线,判断为MA(3)模型;
(2) AR
AR(1): x t = 0.8 x t − 1 + ε t x_t = 0.8x_{t-1}+\varepsilon_t xt=0.8xt−1+εt
AR(2): x t = − x t − 1 − 0.5 x t − 2 + ε t x_t = -x_{t-1}-0.5x_{t-2}+\varepsilon_t xt=−xt−1−0.5xt−2+εt
AR(3): x t = x t − 1 − 0.5 x t − 2 + 0.3 x t − 3 + ε t x_t = x_{t-1} - 0.5x_{t-2} + 0.3x_{t-3}+\varepsilon_t xt=xt−1−0.5xt−2+0.3xt−3+εt
ar1 <- arima.sim(n=1000, list(ar=0.8))
ar2 <- arima.sim(n=1000, list(ar=c(-1,-0.5)))
ar3 <- arima.sim(n=1000, list(ar=c(1,-0.5,0.3)))
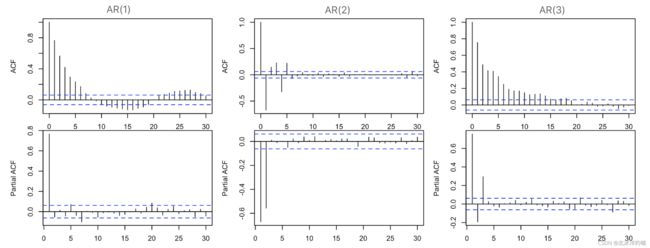
从图倒推,首先ACF图皆为拖尾,可判断未AR或者ARMA模型;再看PACF图:
左边PACF图明显截尾状态,最后一个超出2倍标准差(蓝线)的阶数为1(有1根纵向线超过2倍标准差),故为AR(1)模型;
中间PACF图截尾,最后一个超出2倍标准差(蓝线)的阶数为2,判断为AR(2)模型;
右变PACF图中最后一个超出2倍标准差(蓝线)的阶数为3,判断为AR(3)模型。
(3) ARMA(p,q)
ARMA(1,1): x t = 0.8 x t − 1 + ε t + 0.4 ε t − 1 x_t = 0.8x_{t-1} + \varepsilon_t + 0.4\varepsilon_{t-1} xt=0.8xt−1+εt+0.4εt−1
ARMA(2,1): x t = 0.8 x t − 1 − 0.4 x t − 2 + ε t + 0.4 ε t − 1 x_t = 0.8x_{t-1} - 0.4x_{t-2} + \varepsilon_t + 0.4\varepsilon_{t-1} xt=0.8xt−1−0.4xt−2+εt+0.4εt−1
ARMA(1,2): x t = 0.8 x t − 1 + ε t + 0.4 ε t − 1 + 0.7 ε t − 2 x_t = 0.8x_{t-1} + \varepsilon_t + 0.4\varepsilon_{t-1} + 0.7\varepsilon_{t-2} xt=0.8xt−1+εt+0.4εt−1+0.7εt−2
arma11 <- arima.sim(n=1000,list(sr=0.8,ma=0.4))
arma21 <- arima.sim(n=1000,list(ar=c(0.8, -0.4),ma=0,4))
arma12 <- arima.sim(n=1000,list(ar=0.8, ma=c(0.4,0.7)))

ACF图皆为拖尾,判断为AR模型或ARMA模型;
PACF图也为拖尾,判断为ARMA模型,阶数无法通过ACF和PACF图看出。