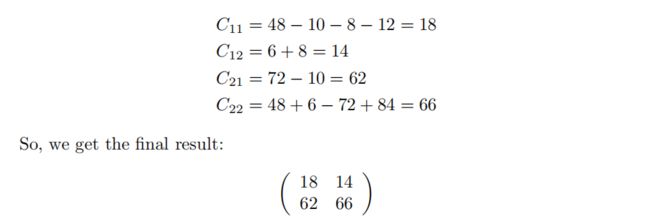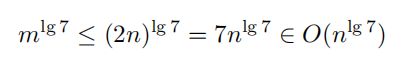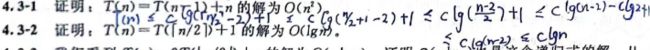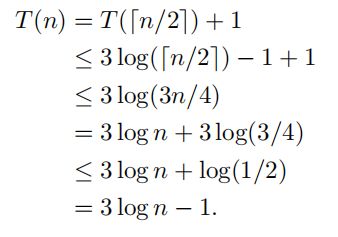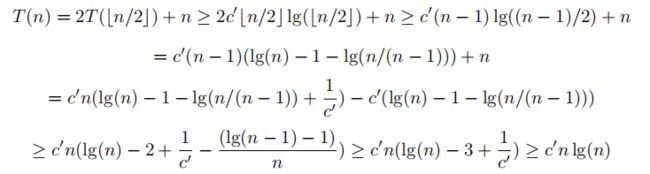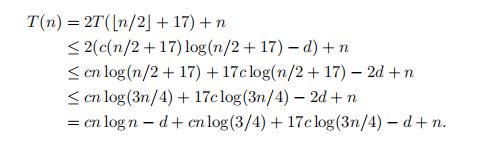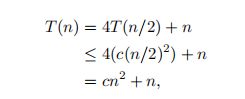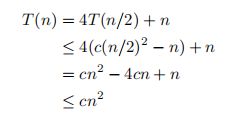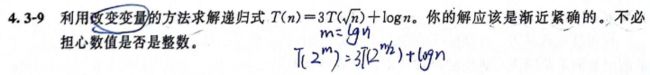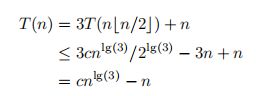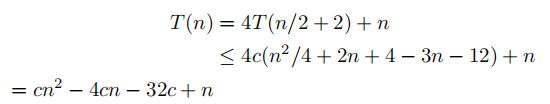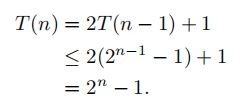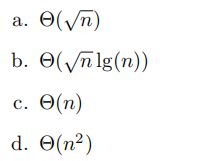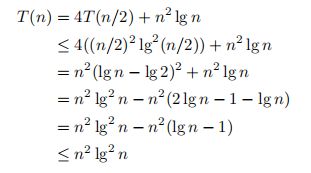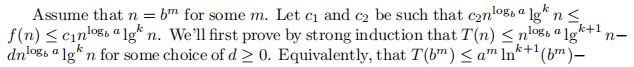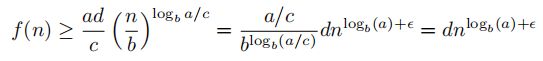算法导论第四章练习参考答案(6) - 4.1-4.6
它会返回最小负的位置。在计算每个交叉和时，最正的交叉和必须具有最短的可能长度。该算法不考虑长度为0的子数组，因此它的长度必须为1。
Exercise 4.1-2
Exercise 4.1-3
交叉点大约是一个长度为20的数组，但是，时间非常嘈杂，而且我认为在运行期间存在垃圾收集，因此它不可靠。使用实际的分析器来测量运行时可能会更有效。通过切换递归算法处理基本情况的方式，递归算法现在更适合较小的n值。包含的图表对于蛮力算法有非常奇怪的运行时间。这些时间是在Core 2双核处理器P8700和java 1.8.0.51上获得的。
在运行时图表中，x轴是数组输入的长度。y轴是以纳秒为单位测量的运行时间。
Exercise 4.1-4
首先对输入数组进行线性扫描，看看它是否包含任何正项。如果是，像往常一样运行算法。否则，返回sum为0的空子数组并终止算法。
Exercise 4.1-5
见算法标记线性时间最大子数组。
Exercise 4.2-1
Exercise 4.2-2
像往常一样，我们假设n是2的幂A和B是n × n矩阵。让我[i . . . j] [k . . .m]表示A的子矩阵由第i到j行和第k到m列组成。
Exercise 4.2-3
你可以把输入矩阵变成2的幂然后运行给定的算法。填充下一个最大的2次幂(称之为m)将最多使n的值翻倍，因为每个2的次幂彼此相差2倍。这将有运行时
和
把这些放在一起，我们得到运行时是Θ(n ^ lg7)。
Exercise 4.2-4
假设对于某个m, n = 3m。然后，使用分块矩阵乘法，我们得到递归运行时间T(n) = kT(n/3)+O(1)。根据主定理，我们需要使log3k < lg7的最大整数k。这个由k = 21给出。
Exercise 4.2-5
如果我们采用这三种算法，并将乘法次数除以提升到lg(7)的矩阵的边长，我们大致得到以下值
374539634167
这意味着，如果作为Strassen算法的基本情况，第一个将在非常大的矩阵中表现最好。
Exercise 4.2-6
通过考虑分块矩阵乘法和使用Strassen算法作为子程序，我们可以用一个kn×n矩阵乘以一个n×kn矩阵，在Θ(k^2 * n^log 7)时间内。通过颠倒顺序，我们可以在Θ(k * n^log 7) 时间的中完成它。
Exercise 4.2-7
我们可以看到，最终的结果应该是
(a + bi)(c + di) = ac−bd + (cb + ad)i
我们将相乘
P1 = (a + b)*c = ac + bcP2 = b*(c + d) = bc + bd
P3 = (a−b)*d = ad + bd
然后，我们可以求出实部通过取P1 - P2和虚部用P2 + P3。
归纳假设T(n)≤c* n^2，令c为max(1, T(1))，则
T(n) = T(n−1)+n ≤ c*(n−1)^2+n = c* n^2 +(1−2c)*n+1 ≤ c* n^2+2−2c ≤ c* n^2。
第一个不等式来源于归纳假设，第二个不等式来源于n≥1且1−2c < 0，最后一个是c≥1。
Exercise 4.3-2
我们会证明T(n)≤3*log n - 1，这意味着T(n) = O(logn)。
Exercise 4.3-3 
归纳假设T(n)≤cn*lgn，其中c = max(T(2)/2 , 1)，则
所以T(n)∈O(nlgn)。
现在，归纳假设T(n)≥c' * nlgn其中c' = min(1/3, T(2)/2) 。
因此，T(n)∈Ω(n)。结合问题的第一部分，我们得到T(n)∈Θ(n)。
Exercise 4.3-4
我们将使用归纳假设T(n)≤2n log n + 1。首先观察到这意味着T(1) = 1，所以基本情况是满足的。然后我们有
Exercise 4.3-5 
如果n是偶数，那么归纳法的这一步与归并排序的“不精确”递归是一样的。假设n是奇数，那么递归式就是T(n) = T((n + 1)/2) + T((n - 1)/2) + Θ(n)。然而，将nlg(n)中的参数移动一半，这最多只会改变函数的值1/2。
，但这是o(n)，所以会被吸收到Θ(n)项中。
Exercise 4.3-6
选择n1，使n≥n1表示n/2+17 ≤ 3n/4。我们会找到c和d使得T(n)≤cn*logn−d。
取c =−2/ log(3/4)， d = 34。那么，我们有T(n)≤cn*log n - d +17 c log (n) - n。由于log(n) = o(n)，因此存在n2，使得n≥n2，意味着n≥17c log(n)。让n0 = max{n1, n2}，我们有n≥n0，意味着T(n)≤cn*log n - d。因此T(n) = O(n log n)。
Exercise 4.3-7
我们首先尝试替换证明T(n)≤c*n ^ log3(4) 。
这显然无法满足≤c*n ^ log3(4)。
现在，假设我们让归纳假设T(n)≤c*n ^ log3(4) - 3*n 。
得证。
Exercise 4.3-8
假设我们想用替换来表示T(n)≤c * n^2对于某个c，我们有
当c > 0时，它不能小于c* n^2。接下来我们将尝试证明T(n)≤c * n^2−n。
假设c≥1/4。
Exercise 4.3-9
考虑2^k的n次方。然后，递归式变成
我们定义S(k) = T(2^k）. 所以,
我们使用归纳假设
根据需要。类似地，我们展示了
我们得到
。
把这个转化回T，
。
所以
Exercise 4.4-1 - Exercise 4.4-5
Exercise 4.4-1递归树中，树的深度是lg(n)，比根低i层的节点数是3^i。这意味着我们估计运行时间是
我们可以通过代入来看出这一点。然后，我们得到
。所以，我们有
。
Exercise 4.4-2
递归树的深度d处只有一个节点，其权值为
。
因为树有log(n)层，猜解大概是
代换法：证明T(n) ≤ c * n^2
假设c≥4/3。
Exercise 4.4-3递归树的深度大约是lg(n)，在根下面的第i层有4^i个顶点，所以猜测是n^2。
代换法：
证明T(n) ≤ cn^2 − 6n。
只要满足 −4c + 1 ≤ −6 和 c ≥ 0， ≤cn^2 - 6成立。即c≥ 7/4，两者都能满足。
Exercise 4.4-4递归树看起来像一个高度为n的完整二叉树，每个节点的代价为1。猜解是O(2^n)。代换法：验证 T( n) ≤ 2^ n − 1.
Exercise 4.4-5
递归树看起来像一个长长的分支，从它的分支一直跳到一半。这看起来是一个很完整的树，我们会猜测运行时间是O(2^n)。
代换法：
证明T(n)≤2^n。
为了证明这实际上是一个很紧的边界，我们将证明我们不可能有任何多项式的上界。也就是说，如果我们有T(n)≤cn^k，那么当我们代入递归式时，我们得到n^k的新系数可以高达
。因此，无论我们如何选择c，它都大于c。
Exercise 4.5-2 
回想一下Strassen算法的运行时间为Θ(n^lg7)。我们选择a = 48。这是使log4(a) < lg7的最大整数。并且，2 < log4(48)，因此存在 q > 0，使得n^2 < n^(log4(48)−q)。根据主定理的情形1,T(n) = Θ(n^log4(48))渐近地优于Θ(n^lg7)。
Exercise 4.5-3
应用a = 1, b = 2的方法，我们得到Θ(n^log2(1)) = Θ(1)。在第二种情况下，我们得到了最终结果Θ(n^log2(1) *lg(n)) = Θ(lg(n))。
Exercise 4.5-4
主方法在这里不能应用。观察到logb(a) = log2(4) = 2 和 f(n) = n^2 * lgn。
很明显，情形1和情形2不适用。进一步，尽管f渐近地大于n^2，它不是多项式地大，所以情况3也不适用。我们会证明T(n) = O(n^2 * (lgn)^2)。
为了做到这一点，我们将归纳证明T(n)≤(n^2) * ((lgn)^2)。
当n>=2。
Exercise 4.5-5 
设 p = a = 1, b = 3, f = 3n + 2^(3n)χ{2^i : :i∈N}，其中χA是集合a的指示函数，那么对于任意数N，如果N是2的3次幂，我们知道
，因此，即使
f∈Ω(n) = Ω(n^(logb(a)+p))，它也不满足正则性条件。
Exercise 4.6-1
Nj是通过将b的第j个位置向右移动得到的，如果第j个最低有效位置有一个非零，则加1。
Exercise 4.6-2
Exercise 4.6-3
假设f满足正则性条件，我们希望∃p，d，k，∀n≥k，有f(n)≥d*n^(loga(b) +p)。由正则性条件可知，当n足够大时，af(n/b)≤cf(n)。特别地，对于所有n≥b*k都成立。设这也是我们上面的k， p = - logb (c)。最后设d为f(n)/n^(logb (a)+p)在bk和b^2 * k之间的最大值。然后，我们将通过归纳法证明，对于最大的i，使得b^i * k小于n，并且对于每一个n≥k， f(n)≥dn^(loga(b) +p)。通过我们对d的定义，我们有它对i = 1成立。假设我们有b^(i - 1)*k < n≤b^i * k。然后，根据规律性和归纳假设，cf(n)≥af(n/b)≥a* d* ( (n/b)^(loga(b) +p) )。解f(n)，我们有
完成归纳。