tinyxml2遍历所有节点_数据结构—二叉树的遍历及重构二叉树【图示详解】

点击蓝字关注我们

AI研习图书馆，发现不一样的精彩世界

数据
结构

二叉树的遍历

之前的一篇文章：数据结构—树|二叉树|前序遍历、中序遍历、后序遍历【图解实现】，只对二叉树的遍历进行了宽泛的描述，这篇随笔重点对二叉树的前、中、后序的遍历顺序进行详细分析，并附代码实现。

一、简介

二叉树的深度优先遍历(DFS)可细分为前序遍历、中序遍历、后序遍历，这三种遍历可以用递归方法实现(本篇随笔主要分析递归实现)，也可使用非递归方法实现。

• 前序遍历：根节点->左子树->右子树(根->左->右)

• 中序遍历：左子树->根节点->右子树(左->根->右)

• 后序遍历：左子树->右子树->根节点(左->右->根)

在进行已知两种遍历顺序求另一种遍历顺序前，我们先来先看一下不同遍历顺序对应的代码。

1. 前序遍历

/* 以递归方式 前序遍历二叉树 */void PreOrderTraverse(BiTree t, int level){    if (t == NULL)    {        return ;    }    printf("data = %c level = %d\n ", t->data, level);    PreOrderTraverse(t->lchild, level + 1);    PreOrderTraverse(t->rchild, level + 1);}

2. 中序遍历

/* 以递归方式 中序遍历二叉树 */void PreOrderTraverse(BiTree t, int level){    if (t == NULL)    {        return ;    }    PreOrderTraverse(t->lchild, level + 1);    printf("data = %c level = %d\n ", t->data, level);    PreOrderTraverse(t->rchild, level + 1);}

3. 后序遍历

/* 以递归方式 后序遍历二叉树 */void PreOrderTraverse(BiTree t, int level){    if (t == NULL)    {        return ;    }    PreOrderTraverse(t->lchild, level + 1);    PreOrderTraverse(t->rchild, level + 1);    printf("data = %c level = %d\n ", t->data, level);}

三种遍历方式对应的代码几乎相同，只是一条语句的位置发生了变化：

printf("data = %c level = %d\n ", t->data, level);

只看文字和代码来理解遍历的过程是比较困难的，建议读者亲自去遍历，为了理清遍历的过程下面上题。

二、案例解析

1. 前序遍历

前序遍历特点：根节点->左子树->右子树

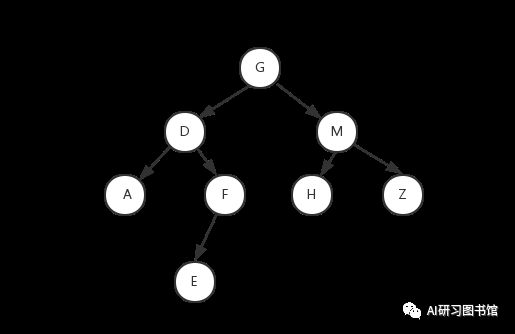
注意看前序遍历的代码，printf语句是放在两条递归语句之前的，所以先访问根节点G，打印G，然后访问左子树D，此时左子树D又作为根节点，打印D，再访问D的左子树A。

A又作为根节点，打印A，A没有左子树或者右子树，函数调用结束返回到D节点,(此时已经打印出来的有：GDA),D节点的左子树已经递归完成，现在递归访问右子树F，F作为根节点，打印F，F有左子树访问左子树E。 E作为 根节点， 打印E， (此时已经打印出来的有： GDAFE )，E没有左子树和右子树，函数递归结束返回F节点，F的左子树已经递归完成了，但没有右子树，所以函数递归结束，返回D节点，D节点的左子树和右子树递归全部完成。 函数递归结束返回G节点，访问G节点的右子树M，M作为根节点，打印M，访问M的左子树H，H作为根节点，打印H，(此时已经打印出来的有：GDAFEMH)H没有左子树和右子树，函数递归结束，返回M节点。 M节点的左子树已经 递归完成，访问右子树Z，Z作为根节点， 打印Z， Z没有左子树和右子树，函数递归结束，返回M节点，M节点的左子树右子树递归全部完成，函数递归结束，返回G节点，G节点的左右子树递归全部完成，整个二叉树的遍历就结束了。 (终于打完了··) 前序遍历结果：GDAFEMHZ

前序遍历步骤

• 第一步：打印该节点

• 第二步：访问左子树，返回到第一步

• 第三步：访问右子树，返回到第一步

• 第四步：结束递归，返回到上一个节点

 前序遍历的另一种表述：

• (1)访问根节点

• (2)前序遍历左子树

• (3)前序遍历右子树

(在完成第2,3步的时候，也是要按照前序遍历二叉树的规则完成)

前序遍历结果：GDAFEMHZ

2. 中序遍历

中序遍历步骤：

• 第一步：访问该节点左子树

• 第二步：若该节点有左子树，则返回第一步，否则打印该节点

• 第三步：若该节点有右子树，则返回第一步，否则结束递归并返回上一节点

简单理解的中序：先左到底，左到不能在左了就停下来并打印该节点，然后返回到该节点的上一节点，并打印该节点，然后再访问该节点的右子树，再左到不能再左了就停下来。

中序遍历的另一种表述：

• (1)中序遍历左子树

• (2)访问根节点

• (3)中序遍历右子树

(在完成第1，3步的时候，要按照中序遍历的规则来完成)

所以该图的中序遍历为：ADEFGHMZ

3. 后序遍历

• 第一步：访问左子树

• 第二步：若该节点有左子树，返回第一步

• 第三步：若该节点有右子树，返回第一步，否则打印该节点并返回上一节点

 后序遍历的另一种表述：

• (1)后序遍历左子树

• (2)后序遍历右子树

• (3)访问根节点

(在完成1,2步的时候，依然要按照后序遍历的规则来完成)

该图的后序遍历为：AEFDHZMG

三、重构二叉树

进入正题，已知两种遍历结果求另一种遍历结果，其实就是重构二叉树。

第一种：已知前序遍历、中序遍历求后序遍历

• 前序遍历：ABCDEF

• 中序遍历：CBDAEF

在进行分析前，读者需要知道不同遍历结果的特点

• 1、前序遍历的第一元素是整个二叉树的根节点

• 2、中序遍历中根节点的左边的元素是左子树，根节点右边的元素是右子树

• 3、后序遍历的最后一个元素是整个二叉树的根节点

用上面这些特点来分析遍历结果：

第一步：先看前序遍历，确定根节点为A

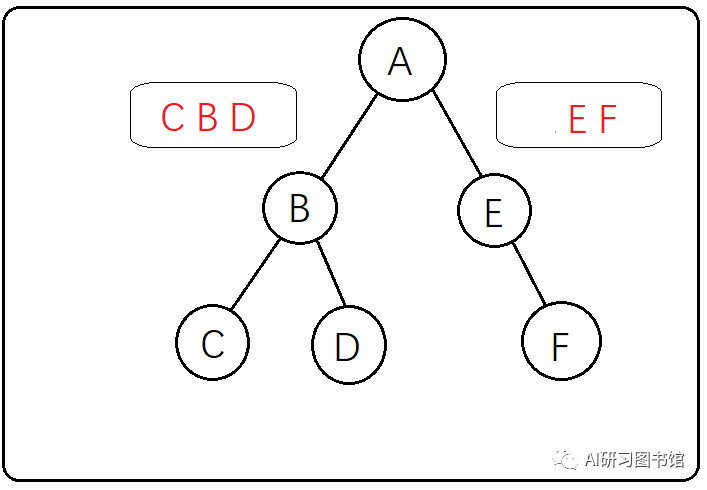
第二步：确认了根节点，再来看中序遍历，中序遍历中根节点A的左边是CBD，右边是EF，所有可以确定二叉树既有左子树又有右子树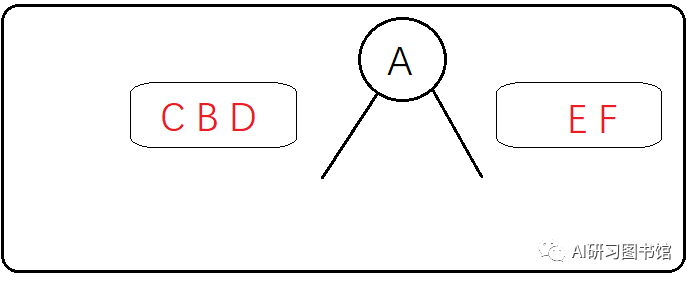

第三步：先来分析左子树CBD，那么CBD谁来做A的左子树呢？这个时候不能直接用中序遍历的特点(左->根->右)得出左子树应该是这个样子。

因为有两种情况都满足中序遍历为CBD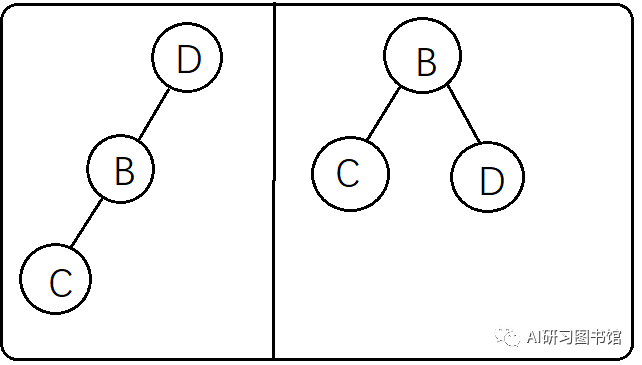 无法直接根据中序遍历来直接得出左子树的结构，这个时候就要返回到前序遍历中去 观察前序遍历ABCDEF，左子树CBD在前序遍历中的顺序是BCD，意味着B是左子树的根节点(B是A的左子树),得出这个结果是因为如果一个二叉树的根节点有左子树，那么 这个左子树一定在前序遍历中一定紧跟着根节点(这个是用前序遍历的特点(根->左->右)得出的),到这里就可以确认 B 是左子树的根节点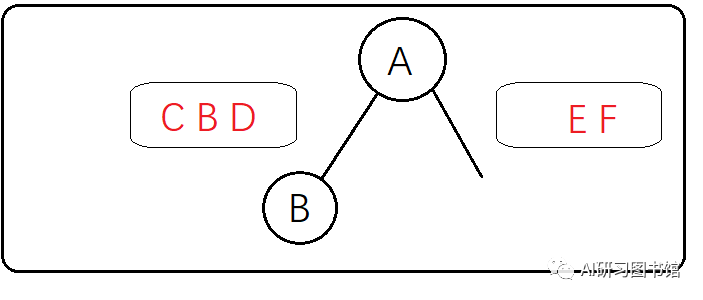

第四步：再观察中序遍历CBDAEF，B左边是C右边是D，说明B节点既有左子树又有右子树，左右子树只有一个元素就可以直接确定了，不用再返回去观察前序遍历

第五步：到这里左子树的重建就已经完成了，现在重建右子树。观察中序遍历右子树为EF，再观察前序遍历ABCDEF中右子树的顺序为EF，所以E为A的右子树，再观察中序便利中E只有右边有F，所有F为E的右子树，最后得到的二叉树是这个样子的。

所有求得的后序遍历为：CDBFEA 总结一下上述步骤： 先观察前序遍历找到根节点->观察中序遍历将根节点左边归为左子树元素，右边归为右子树元素(可能会出现只有左子树或者右子树的情况)->观察前序遍历中左\右子树几个元素的顺序，最靠前的为左\右子树的根节点->重复前面的步骤。

第二种：已知中序遍历、后序遍历求前序遍历

• 中序遍历：CBDAEF

• 后序遍历为：CDBFEA

仍然是根据不同遍历方式结果的特点来重构二叉树，过程很相似这里就不详细说了。 后序遍历的最后一个元素A是根节点，在中序遍历中以根节点A作为分界将元素分为左子树(CBD)和右子树(EF)；再观察后序遍历中左子树的顺序是CDB， 可以判断出B是左子树的根节点(因为后序遍历是：左->右->根)，再观察中序遍历，B元素左边是C右边是D，说明B节点既有左子树又有右子树，左右子树只有一个元素就可以直接确定了，不用再返回去观察后序遍历， 左子树 重建完成。 现在来看右子树，右子树有两个元素EF，观察后序遍历E在F的后面，所以E是右子树的根节点，然后看中序遍历中E只有右边一个F元素了，即F是E的 右子树 ，此时整个二叉树重构完成。   总结一下上述步骤： 先观察后序遍历找到根节点->观察中序遍历将根节点左边归为左子树元素，右边归为右子树元素(可能会出现只有左子树或者右子树的情况)->观察后序遍历中左\右子树几个元素的顺序，最靠后的为左\右子树的根节点->重复前面的步骤。 注意： 已知前序遍历、后序遍历无法求出中序遍历(因为由前序后序重构出来的二叉树不止一种)。 举个栗子：

如上图所示，这两种二叉树前序(BEFA)和后序(AFEB)一样，但对应的中序遍历结果却不一样(左边是AFEB，右边是BEFA)，所以仅靠前序和后序无法重构出唯一的二叉树。

综上所述，今天主要讲解了二叉树的遍历及重构二叉树，相信聪明的你已经学会了！

更多数据结构精彩分享，敬请期待！

Bilibili : 洛必达数数CSDN博客：算法之美DLGitHub：statisticszhang

关注AI研习图书馆，发现不一样的精彩世界