算法：给出指定整数区间、期望值，得到最终结果

1，问题： 

在游戏中，我们经常会遇到以下情况：打开宝箱，获得x个卡牌碎片。

  但通常策划只会给一个既定的数值空间，和一个期望得到的值，然后让我们去随机。比如：

  问题A：在1~3之间的整数中随机，期望随机结果的平均值是1.175，如何实现？
  延伸：1~10之间，期望平均值是5.4呢？
  以上问题可以归纳为：m~n之间，期望值是q，求出最终结果。

  首先，我们可以问下AI，如何实现这个算法。以下是AI给出结果的截图：

  这种按照多元方程求解的方法，需要自己去随机给定概率，当然可以实现。但有没有更直接的方法呢？

2，求解过程：

  经过思考，我们可以用补偿算法的方式，来得到这个既定结果。这里需要引入一个补偿数的概念，补偿数由每次随机结果的偏差值累加而成。

  因为每次随机事件是独立的，我们引入问题A，得到如下随机结果：

第1次随机区间1~3，随机结果1，补偿数为 0.175 ；

第二次随机区间2~3，随机结果2，补偿数为-0.65；

第3次随机区间1~2，随机结果1，补偿数为-0.475，小于精度0.5，取随机数组结束。

随机数组为1,2,1；在其中随机取1位便是结果。

  我们可以验算下：（1+2+1）/3~=1.333，与1.175偏差小于0.5。代码编译：

  然后我们将以上思考过程改为函数如下：

 //获取所有的随机范围
    void GetAllRandom(float _expect, int _min, int _max, float _precision)
    {
        var _getList = new List();
        GetRandomOnce(_getList, 0, 0f, _expect, _min, _max, _precision);


        var _f = 0f;
        var _str = "";
        foreach (var idx in _getList)
        {
            _f += idx;
            _str += idx + ",";
        }
        Debug.LogError("得到结果数组：" + _str + "\n平均值：" + (_f / _getList.Count));

        Debug.LogError("最终结果：" + _getList[Random.Range(0, _getList.Count)]);
    }



    /// 

    /// 取到的随机数 数组
    /// 
    /// 取值数组
    /// 随机次数
    /// 补偿值：累加
    /// 期望值
    /// 最小值
    /// 最大值
    /// 精确度
    /// 约束条件：
    /// 1，随机次数>n次，比如1~10之间随机，随机次数需要>10
    /// 2,最终补偿数需要误差小于1（精确度）   
    private void GetRandomOnce(List _list, int _ranNum, float _compensate, float _expect, int _min, int _max, float _precision)
    {
        //根据补偿数重新定义范围
        int _ran = 0;
        if (_compensate > 0f)
        {
            var _tMin = Mathf.Min(_max, Mathf.CeilToInt(_min + _compensate));
            _ran = Random.Range(_tMin, _max + 1);
            Debug.Log(_tMin + "   " + _ran + "  " + _max);

        }
        else
        {
            var _tMax = Mathf.Max(_min, Mathf.FloorToInt(_max + _compensate));
            _ran = Random.Range(_min, _tMax + 1);
            Debug.Log(_min + "  " + _ran + "   " + _tMax);
        }
        _compensate += _expect - _ran;
        _ranNum++;
        Debug.LogError(_ran + "   " + _compensate+"   "+_ranNum);
        _list.Add(_ran);
        if (_ranNum > (_max - _min + 1) && Mathf.Abs(_compensate) < _precision) return;//满足约束条件

        if (_ranNum > 100) { _list.Clear();_list.Add((int)_expect);return; }//防止意外

        GetRandomOnce(_list, _ranNum, _compensate, _expect, _min, _max, _precision);

    }

3，测试

  写个简单方法测试下：

    public int min = 1;//区间最小值
    public int max = 3;//区间最大值
    public float expect = 1.175f;//期望值

    public float precision = 0.5;//精度

   void Update()
    {
        if (Input.GetKeyDown(KeyCode.A))
        {
            GetAllRandom(expect, min, max, precision);
        }
    }

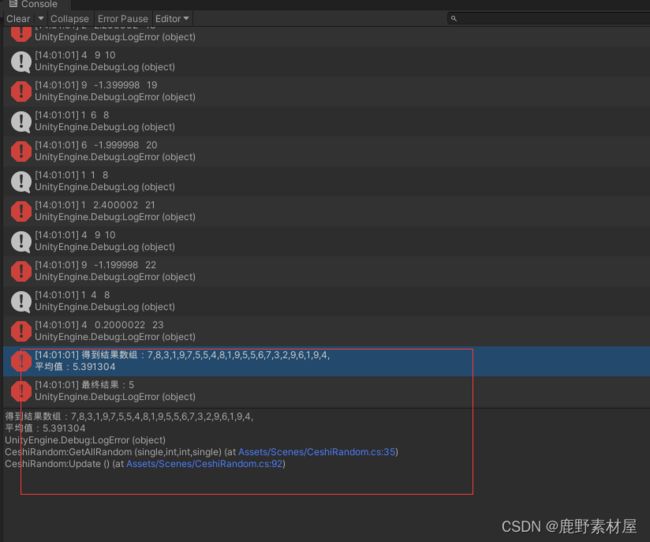
  得到结果如下：

  当然我们有时候不想随机那么多步骤（纯随机的不确定性），还可以添加更多的约束。

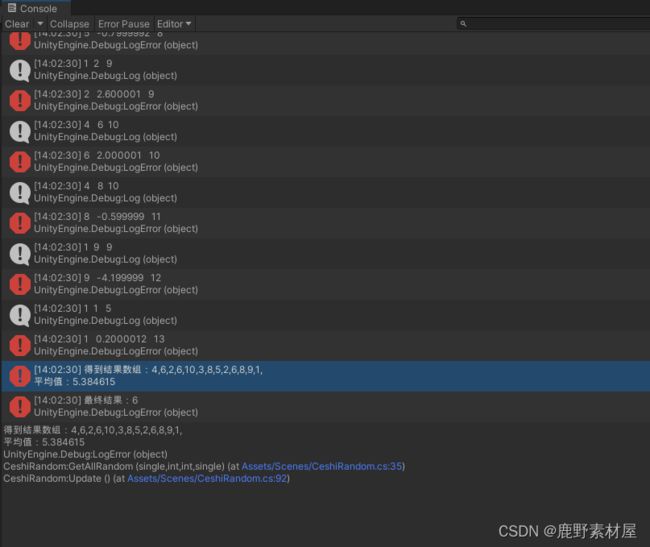
  最后，我们代入扩展再测试下。电脑给出的随机结果如下：

  经过多次测试，实验结果是逼近期望值的（不过取越靠近中间数的话，独立事件的结果偏差可能越大，这里最好再加上一层约束）。