_30LeetCode代码随想录算法训练营第三十天-贪心算法 | 860.柠檬水找零 、406.根据身高重建队列、452.用最少数量的箭引爆气球
_30LeetCode代码随想录算法训练营第三十天-贪心算法 | 860.柠檬水找零 、406.根据身高重建队列、452.用最少数量的箭引爆气球
题目列表
- 860.柠檬水找零
- 406.根据身高重建队列
- 452.用最少数量的箭引爆气球
860.柠檬水找零
代码随想录地址:https://programmercarl.com/0860.%E6%9F%A0%E6%AA%AC%E6%B0%B4%E6%89%BE%E9%9B%B6.html
题目
在柠檬水摊上,每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品,(按账单 bills 支付的顺序)一次购买一杯。
每位顾客只买一杯柠檬水,然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零,也就是说净交易是每位顾客向你支付 5 美元。
注意,一开始你手头没有任何零钱。
给你一个整数数组 bills ,其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零,返回 true ,否则返回 false 。
示例 1:
输入:bills = [5,5,5,10,20]
输出:true
解释:
前 3 位顾客那里,我们按顺序收取 3 张 5 美元的钞票。
第 4 位顾客那里,我们收取一张 10 美元的钞票,并返还 5 美元。
第 5 位顾客那里,我们找还一张 10 美元的钞票和一张 5 美元的钞票。
由于所有客户都得到了正确的找零,所以我们输出 true。
示例 2:
输入:bills = [5,5,10,10,20]
输出:false
解释:
前 2 位顾客那里,我们按顺序收取 2 张 5 美元的钞票。
对于接下来的 2 位顾客,我们收取一张 10 美元的钞票,然后返还 5 美元。
对于最后一位顾客,我们无法退回 15 美元,因为我们现在只有两张 10 美元的钞票。
由于不是每位顾客都得到了正确的找零,所以答案是 false。
提示:
- 1 <= bills.length <= 1 0 5 10^5 105
bills[i]不是5就是10或是20
思路
- 情况一:账单是5,直接收下。
- 情况二:账单是10,消耗一个5,增加一个10
- 情况三:账单是20,优先消耗一个10和一个5,如果不够,再消耗三个5(为什么先消耗十块,因为五块的用处更多,此处有贪心的成分在)
代码
/*
* @lc app=leetcode.cn id=860 lang=cpp
*
* [860] 柠檬水找零
*/
// @lc code=start
class Solution {
public:
bool lemonadeChange(vector<int>& bills) {
int five = 0;
int ten = 0;
for(int bill : bills)
{
if(bill == 5)
five++;
else if(bill == 10)
{
if(!five) return false;
ten++;
five--;//消耗掉一个五块的找零
}
else
{
//优先消耗掉10块的找零,因为5块的用处更多
if(five && ten)
{
ten--;
five--;
}
else if(five >= 3)//没有10块的就全部使用五块的找零
five -= 3;
else
return false;
}
}
return true;
}
};
// @lc code=end
406.根据身高重建队列
代码随想录地址:https://programmercarl.com/0406.%E6%A0%B9%E6%8D%AE%E8%BA%AB%E9%AB%98%E9%87%8D%E5%BB%BA%E9%98%9F%E5%88%97.html
题目
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释:
编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
示例 2:
输入:people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
输出:[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]
提示:
1 <= people.length <= 2000- 0 <= h i h_i hi <= 1 0 6 10^6 106
- 0 <= k i k_i ki < people.length
- 题目数据确保队列可以被重建
思路
关于我没看懂题目:不懂的点在于不能改变 k i k_i ki的值。
然后:
局部最优:优先按身高高的people的k来插入。插入操作过后的people满足队列属性
全局最优:最后都做完插入操作,整个队列满足题目队列属性
代码
使用数组:
- 时间复杂度:O(nlog n + n^2)
- 空间复杂度:O(n)
但使用vector是非常费时的,C++中vector(可以理解是一个动态数组,底层是普通数组实现的)如果插入元素大于预先普通数组大小,vector底部会有一个扩容的操作,即申请两倍于原先普通数组的大小,然后把数据拷贝到另一个更大的数组上。
所以使用vector(动态数组)来insert,是费时的,插入再拷贝的话,单纯一个插入的操作就是O(n2)了,甚至可能拷贝好几次,就不止O(n2)了。
class Solution {
public:
static bool cmp(vector<int>& a, vector<int>& b)
{
if(a[0] == b[0])
return a[1] < b[1];
else
return a[0] > b[0];
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
//首先按 首先从大到小对h进行排序,其次从小到大对k进行排序 的规则对people进行排序
sort(people.begin(), people.end(), cmp);
//定义数组
vector<vector<int>> res;
//以k的大小为index插入结果数组
for(vector<int> data : people)
{
int index = data[1];
res.insert(res.begin() + index, data);
}
return res;
}
};
使用链表:执行时间确实变低了
- 时间复杂度:O(nlog n + n^2)
- 空间复杂度:O(n)
class Solution {
public:
static bool cmp(vector<int>& a, vector<int>& b)
{
if(a[0] == b[0])
return a[1] < b[1];
else
return a[0] > b[0];
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
//首先按 首先从大到小对h进行排序,其次从小到大对k进行排序 的规则对people进行排序
sort(people.begin(), people.end(), cmp);
//定义数组
list<vector<int>> res;
//以k的大小为index插入结果数组
for(vector<int> data : people)
{
int index = data[1];
std::list<vector<int>>::iterator it = res.begin();
while(index--)
it++;
res.insert(it, data);
}
return vector<vector<int>>(res.begin(), res.end());
}
};
452.用最少数量的箭引爆气球
代码随想录地址:https://programmercarl.com/0452.%E7%94%A8%E6%9C%80%E5%B0%91%E6%95%B0%E9%87%8F%E7%9A%84%E7%AE%AD%E5%BC%95%E7%88%86%E6%B0%94%E7%90%83.html
题目
有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,其中points[i] = [ x s t a r t x_{start} xstart, x e n d x_{end} xend]表示水平直径在 x s t a r t x_{start} xstart 和 x e n d x_{end} xend之间的气球。你不知道气球的确切 y 坐标。
一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 x s t a r t x_{start} xstart, x e n d x_{end} xend, 且满足 x s t a r t x_{start} xstart ≤ x ≤ x e n d x_{end} xend则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后,可以无限地前进。
给你一个数组 points ,返回引爆所有气球所必须射出的 最小 弓箭数。
示例 1:
输入:points = [[10,16],[2,8],[1,6],[7,12]]
输出:2
解释:气球可以用2支箭来爆破:
-在x = 6处射出箭,击破气球[2,8]和[1,6]。
-在x = 11处发射箭,击破气球[10,16]和[7,12]。
示例 2:
输入:points = [[1,2],[3,4],[5,6],[7,8]]
输出:4
解释:每个气球需要射出一支箭,总共需要4支箭。
示例 3:
输入:points = [[1,2],[2,3],[3,4],[4,5]]
输出:2
解释:气球可以用2支箭来爆破:
- 在x = 2处发射箭,击破气球[1,2]和[2,3]。
- 在x = 4处射出箭,击破气球[3,4]和[4,5]。
提示:
- 1 <= points.length <= 1 0 5 10^5 105
points[i].length == 2- − 2 31 -2^{31} −231 <= x s t a r t x_{start} xstart < x e n d x_{end} xend <= 2 31 2^{31} 231 - 1
思路
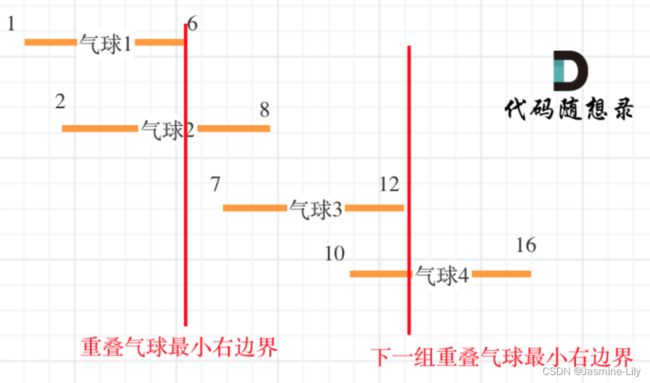
弓箭最少,那么就代表重叠最多。
局部最优:当气球出现重叠,一起射,所用弓箭最少。
全局最优:把所有气球射爆所用弓箭最少。
如果气球重叠了,重叠气球中右边边界的最小值 之前的区间一定需要一个弓箭。
代码
- 时间复杂度:O(nlog n),因为有一个快排
- 空间复杂度:O(1),有一个快排,最差情况(倒序)时,需要n次递归调用。因此确实需要O(n)的栈空间
class Solution {
public:
//从小到大排序
static bool cmp(const vector<int>& a, const vector<int>& b)
{
return a[0] < b[0];
}
int findMinArrowShots(vector<vector<int>>& points) {
//如果points为空,则不需要箭
if(points.size() == 0)
return 0;
//按前区间从小到大排序
sort(points.begin(), points.end(), cmp);
int res = 1;//points不为空则至少需要一只箭
for(int i = 1; i < points.size(); i++)
{
//两个气球不挨着,则需要一只箭
if(points[i][0] > points[i - 1][1])
res++;
else//两个气球挨着
points[i][1] = min(points[i][1], points[i - 1][1]);//更新最小右边界
}
return res;
}
};