【算法专题】卡特兰数

卡特兰数

1. 概述

• 卡特兰数：首先这个一个数，很多问题的结果都是卡特兰数，比如2016年全国三卷数学选择题压轴题让求解的就是卡特兰数，问题如下：

• 首先是结论：卡特兰数为:

$$\frac{C_{2n}^n}{n+1}$$

• 因此，对于上面的题目，结果就是

$$\frac{C_{2m}^m}{m+1}=\frac{C_8^4}{4+1}=\frac{70}{5}=14$$

因此选择C。

---

• 下面看一下卡特兰数的公式是如何推导出来的。首先我们需要将上述问题转换成一个等价的问题：在一个二维平面内，从(0, 0)出发到达(n, n)，每次可以向上或者向右走一格，0代表向右走一个，1代表向上走一格，则每条路径都会代表一个01序列，则满足任意前缀中0的个数不少于1个数序列对应的路径则右下侧，如下图：

符合要求的路径必须严格在上图中红色线的下面（不可以碰到图中的红线，可以碰到绿线）。则我们考虑任意一条不合法路径，例如下图：

所有路径的条数为 $C_{2n}^n$，其中不合法的路径有 $C_{2n}^{n-1}$ 条，因此合法路径有：
$$\begin{gathered} C_{2n}^n-C_{2n}^{n-1}=\frac{(2n)!}{n!\times n!}-\frac{(2n)!}{(n+1)!\times (n-1)!} \\ =\frac{(2n)!\times (n+1)}{n!\times (n+1)!}-\frac{(2n)!\times n}{n!\times (n+1)!} \\ =\frac{(2n)!\times (n+1)-(2n)!\times n}{n!\times (n+1)!} \\ =\frac{(2n)!}{n!\times (n+1)!}=\frac{1}{n+1}\times \frac{(2n)!}{n!\times n!} \\ =\frac{C_{2n}^n}{n+1} \end{gathered}$$
推导完毕。

• 可以看到求解卡塔兰数过程中需要求解组合数，关于组合数的各种求法可以参考：组合数。

• 除了上述两种问题，如下问题对应的答案也是卡特兰数：

  （1）n个结点的二叉树数量h(n) ；其实有递推公式，即：
  $$h(n)=\sum _{i=1}^{n}h(i-1)\times h(n-i)h(0)=1$$
  （2）矩阵链乘：$P=A_1\times A_2\times ...\times A_n$，有多少种不同的计算次序？（相当于加括号，问合法括号序列有多少个）

  （3）一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列?

  （4）有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)

• 补充内容，卡特兰数大小和n的关系：

---

• 卡特兰数的前10项为：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862。可以到网站 oeis 查询各种数列，输入数列的连续几项即可。

---

这里总结一下如何求组合数：

$$C_n^m=\frac{n\times (n-1)\times ...\times (n-m+1)}{1\times 2\times ...\times m}\text{\hspace{1em}(1)}$$

$$C_n^m=\frac{n!}{m!\times (n-m)!}\text{\hspace{1em}(2)}$$

• 如果最终的结果需要对一个数P取余：

  • 递推，$O(n^2)$；

  • 快速幂求逆元（费马小定理），要求P必须是质数，$O(n\times log(n))$，根据公式（1）求解；AcWing 889. 满足条件的01序列、AcWing 2641. 字符串。

  • 质因数分解，不要求P必须是质数，$O(n)$，根据公式（2）求解；AcWing 2641. 字符串、AcWing 1316. 有趣的数列。

• 不要对某个数取余，则需要输出精确解：

  • 递推，没有超过long long的存储范围的话，可以使用；AcWing 415. 栈、AcWing 1645. 不同的二叉搜索树。

  • 模拟，按照公式（1）进行模拟，需要使用高精度；AcWing 1257. 二叉树计数、AcWing 1317. 树屋阶梯。

  • 质因数分解，按照公式（2）进行阶乘质因数分解，然后只使用高精度乘法求解；AcWing 130. 火车进出栈问题、AcWing 1315. 网格。

在高精度求解的过程中使用压位的技巧，加快计算速度。

补充：质因数分解时间复杂度为O(n)的分析

最后一种方法时间复杂度分析：首先要筛质数（$O(n)$的）；然后枚举每个质数，计算出现次数，这一步时间复杂度为：
$$lo{g}_2(n)+lo{g}_3(n)+...+lo{g}_5(n)+lo{g}_t(n)$$
其中t是小于等于n的最大的质数，因为1~n中质数的个数大约为 $\frac{n}{log(n)}$ 个，因此上式：
$$lo{g}_2(n)+lo{g}_3(n)+...+lo{g}_5(n)+lo{g}_t(n)<log(n)+log(n)+...+log(n)+log(n)\approx \frac{n}{log(n)}\times log(n)=n$$
因此时间复杂度大约是$O(n)$的。

2. 例题

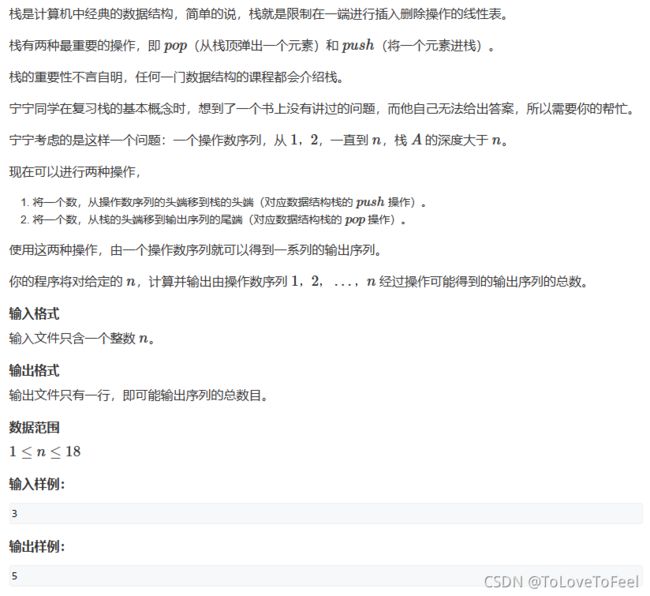
AcWing 415. 栈

问题描述

• 问题链接：AcWing 415. 栈

  

分析

• 卡特兰数。关于卡特兰数的讲解可以参考：组合数。

• 卡特兰数存在公式，如下：

$$f[n]=\frac{C_{2n}^n}{n+1}$$

• 合法的操作序列需要满足：任意前缀中push的操作要大于等于pop的操作。这个问题对应的就是卡特兰数。

• 因为本题n的范围很小，因此可以直接递推求组合数，时间复杂度是：$O(n^2)$。

代码

• C++

#include 

using namespace std;

typedef long long LL;

const int N = 40;

int n;
LL C[N][N];

int main() {
    
    cin >> n;
    
    for (int i = 0; i < N; i++)
        for (int j = 0; j <= i; j++)
            if (!j) C[i][j] = 1;
            else C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
    
    cout << C[n * 2][n] / (n + 1) << endl;
    
    return 0;
}

AcWing 889. 满足条件的01序列

问题描述

• 问题链接：AcWing 889. 满足条件的01序列

  

分析

• 本题让求卡特兰数，直接带入公式即可：

$$\frac{C_{2n}^n}{n+1}=\frac{1}{n+1}\times \frac{a\times (a-1)\times ...\times (a-b+1)}{1\times 2\times ...\times b}a=2n,b=n$$

• 因为这里的n最大为$10^5$，使用递推求组合数是不可取的，因此需要使用上述公式求解组合数，因为牵涉到除法，但是：

$$\frac{a}{b}(modp)\ne \frac{a(modp)}{b(modp)}$$

• 因此需要求解除数对模数的逆元，因为mod是质数，因此任何数与mod都互质，可以使用快速幂求逆元（费马小定理），否则需要使用扩展欧几里得算法求逆元。

• 关于求解快速幂逆元可以参考：快速幂。

• 因为快速幂的时间复杂度为$O(log(n))$，因此本题的时间复杂度为：$O(n\times log(n))$。

代码

• C++

#include 

using namespace std;

typedef long long LL;

const int mod = 1e9 + 7;

int qmi(int a, int k, int p) {
    
    int res = 1 % p;
    while (k) {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

int main() {
    
    int n;
    cin >> n;
    
    int a = 2 * n, b = n;
    int res = 1;
    
    for (int i = a; i > a - b; i--) res = (LL)res * i % mod;
    for (int i = 1; i <= b; i++) res = (LL)res * qmi(i, mod - 2, mod) % mod;
    
    res = (LL)res * qmi(n + 1, mod - 2, mod) % mod;
    
    cout << res << endl;
    
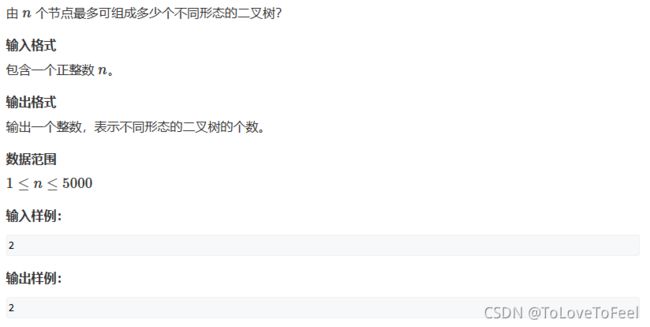
    return 0;
}

AcWing 1257. 二叉树计数

问题描述

• 问题链接：AcWing 1257. 二叉树计数

分析

• 设h(n)表示n个节点可以构成的不同形态的二叉树数目，选择一个节点作为根节点，其左右子树节点数目为i-1、n-i（i范围是[1,n]），因此根据乘法原理，这样的二叉树形态个数为 $h(i-1)\times h(n-i)$，根据加法原理，有：

$$h(n)=\sum _{i=1}^{n}h(i-1)\times h(n-i)h(0)=1$$

• 可以看出就是卡特兰数。

• 但是本题n最大为5000，而且我们要具体输出卡特兰数的大小，因此需要写高精度，按照如下公式求解即可：

$$\frac{C_{2n}^n}{n+1}=\frac{1}{n+1}\times \frac{a\times (a-1)\times ...\times (a-b+1)}{1\times 2\times ...\times b}a=2n,b=n$$

代码

• C++

#include 
#include 

using namespace std;

void mul(vector<int> &a, int b) {
    
    int t = 0;
    for (int i = 0; i < a.size(); i++) {
        t += a[i] * b;
        a[i] = t % 10;
        t /= 10;
    }
    while (t) {
        a.push_back(t % 10);
        t /= 10;
    }
}

void div(vector<int> &a, int b) {
    
    int t = 0;  // 每次除以b后的余数
    for (int i = a.size() - 1; i >= 0; i--) {
        t = t * 10 + a[i];
        a[i] = t / b;
        t %= b;
    }
    while (a.back() == 0) a.pop_back();
}

int main() {
    
    int n;
    cin >> n;
    
    int a = n * 2, b = n;
    
    vector<int> res(1, 1);
    for (int i = a, j = 1; j <= b; i--, j++) {
        mul(res, i);
        div(res, j);
    }
    div(res, n + 1);
    
    for (int i = res.size() - 1; ~i; i--) cout << res[i];
    cout << endl;
    
    return 0;
}

AcWing 1645. 不同的二叉搜索树

问题描述

• 问题链接：AcWing 1645. 不同的二叉搜索树

  

分析

• 卡特兰数。关于卡特兰数的讲解可以参考：组合数。

• 存在递推公式：

$$f[i]=\sum _{k=0}^{i-1}f[k]\times f[i-1-k]$$

代码

• C++

#include 

using namespace std;

typedef long long LL;

const int N = 1010, MOD = 1e9 + 7;

int n;
int f[N];

int main() {
    
    cin >> n;
    
    f[0] = 1;
    for (int i = 1; i <= n; i++)
        for (int k = 0; k < i; k++)
            f[i] = (f[i] + (LL)f[k] * f[i - 1 - k]) % MOD;
    
    cout << f[n] << endl;
    
    return 0;
}

AcWing 130. 火车进出栈问题

问题描述

• 问题链接：AcWing 130. 火车进出栈问题

分析

• 进站看做0，出栈看做1，则任意时刻0的个数不能少于1的个数，因此本题就是AcWing 889. 满足条件的01序列。

• 但是本题需要写一个高精度，需要精确输出可能的排列方式。由于本题n的最大值为六万，很大，因此不能使用直接带入如下公式的方式求解：

$$\frac{C_{2n}^n}{n+1}=\frac{1}{n+1}\times \frac{a\times (a-1)\times ...\times (a-b+1)}{1\times 2\times ...\times b}a=2n,b=n$$

• 这里做的思路是考虑下式：

$$f(n)=\frac{C_{2n}^n}{n+1}=\frac{1}{n+1}\times \frac{(2n)!}{n!\times n!}$$

• 对上式进行质因数分解，得到f(n)的质因数分解表示，因为n最大为六万，所以2n最大为12万，因此筛质数需要筛到12万，关于筛质数可以参考：质数。

• 另外还需要求解n!中质因子p的个数，这个对应题目：AcWing 197. 阶乘分解。在n!的质因数分解中质数p出现的次数为：

$$\lfloor \frac{n}{p}\rfloor +\lfloor \frac{n}{p^2}\rfloor +\lfloor \frac{n}{p^3}\rfloor +......$$

• 之后使用高精度将所有的质因数乘起来即可。为了提高运行速度，这里在高精度的过程中使用压位，因为是long long，这里压8位。关于压位可以参考：高精度之压位。

代码

• C++

// vector存储答案
#include 
#include 

using namespace std;

const int N = 120010;

typedef long long LL;

int primes[N], cnt;
bool st[N];
int sum[N];  // 存储f(n)质因数分解中primes[i]出现的次数

void get_primes(int n) {  // 埃式筛法
    
    for (int i = 2; i <= n; i++) {
        if (!st[i]) {
            primes[cnt++] = i;
            for (int j = i + i; j <= n; j += i) st[j] = true;
        }
    }
}

int get(int n, int p) {
    
    int res = 0;
    while (n) res += n / p, n /= p;
    return res;
}

void mul(vector<LL> &a, int b) {
    
    LL t = 0;
    for (int i = 0; i < a.size(); i++) {
        t += a[i] * b;
        a[i] = t % 100000000;
        t /= 100000000;
    }
    while (t) {
        a.push_back(t % 100000000);
        t /= 100000000;
    }
}

void out(vector<LL> a) {
    
    printf("%lld", a.back());
    for (int i = a.size() - 2; ~i; i--) printf("%08lld", a[i]);
    puts("");
}

int main() {
    
    int n;
    scanf("%d", &n);
    
    int a = n * 2, b = n;
    
    // C(a, b) / (n + 1)
    get_primes(a);
    
    for (int i = 0; i < cnt; i++) {
        int p = primes[i];
        sum[i] = get(a, p) - get(b, p) - get(a - b, p);
    }
    int k = n + 1;
    for (int i = 0; i < cnt && primes[i] <= k; i++) {
        while (k % primes[i] == 0) {
            k /= primes[i];
            sum[i]--;
        }
    }
    
    vector<LL> res(1, 1);
    for (int i = 0; i < cnt; i++) 
        for (int j = 0; j < sum[i]; j++) 
            mul(res, primes[i]);
    
    out(res);
    
    return 0;
}

// 数组存储答案
#include 
#include 

using namespace std;

const int N = 120010;

typedef long long LL;

int primes[N], cnt;
bool st[N];
int sum[N];

LL res[N], tt;  // 存储结果

void get_primes(int n) {
    
    for (int i = 2; i <= n; i++) {  // 线性筛法
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] <= n / i; j++) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

int get(int n, int p) {
    
    int res = 0;
    while (n) res += n / p, n /= p;
    return res;
}

void mul(int b) {
    
    LL t = 0;
    for (int i = 0; i <= tt; i++) {
        t += res[i] * b;
        res[i] = t % 100000000;
        t /= 100000000;
    }
    while (t) {
        res[++tt] = t % 100000000;
        t /= 100000000;
    }
}

void out() {
    
    printf("%lld", res[tt]);
    for (int i = tt - 1; ~i; i--) printf("%08lld", res[i]);
    puts("");
}

int main() {
    
    int n;
    scanf("%d", &n);
    
    int a = n * 2, b = n;
    
    // C(a, b) / (n + 1)
    get_primes(a);
    
    for (int i = 0; i < cnt; i++) {
        int p = primes[i];
        sum[i] = get(a, p) - get(b, p) - get(a - b, p);
    }
    int k = n + 1;
    for (int i = 0; i < cnt && primes[i] <= k; i++) {
        while (k % primes[i] == 0) {
            k /= primes[i];
            sum[i]--;
        }
    }
    
    res[0] = 1;
    for (int i = 0; i < cnt; i++) 
        for (int j = 0; j < sum[i]; j++) 
            mul(primes[i]);
    
    out();
    
    return 0;
}

AcWing 1317. 树屋阶梯

问题描述

• 问题链接：AcWing 1317. 树屋阶梯

分析

• 假设当前我们站在第i个台阶上（台阶编号从1开始），则下方需要i-1个阶梯，上方需要n-i个阶梯，因此如果h(n)表示n阶台阶的搭建方式，则：

$$h(n)=\sum _{i=1}^{n}h(i-1)\times h(n-i)h(0)=1$$

• 当n=3时，有：$h(3)=h(0)\times h(2)+h(1)\times h(1)+h(2)\times h(0)$，其中 $h(0)\times h(2)$表示上图中的情况1、2，$h(1)\times h(1)$表示上图中的情况3，$h(2)\times h(0)$表示上图中的情况4、5。

• 使用高精度求解卡特兰数即可，代码和AcWing 1257. 二叉树计数完全一样。

代码

• C++

#include 
#include 

using namespace std;

void mul(vector<int> &a, int b) {
    
    int t = 0;
    for (int i = 0; i < a.size(); i++) {
        t += a[i] * b;
        a[i] = t % 10;
        t /= 10;
    }
    while (t) {
        a.push_back(t % 10);
        t /= 10;
    }
}

void div(vector<int> &a, int b) {
    
    int t = 0;  // 每次除以b后的余数
    for (int i = a.size() - 1; i >= 0; i--) {
        t = t * 10 + a[i];
        a[i] = t / b;
        t %= b;
    }
    while (a.back() == 0) a.pop_back();
}

int main() {
    
    int n;
    cin >> n;
    
    int a = n * 2, b = n;
    
    vector<int> res(1, 1);
    for (int i = a, j = 1; j <= b; i--, j++) {
        mul(res, i);
        div(res, j);
    }
    div(res, n + 1);
    
    for (int i = res.size() - 1; ~i; i--) cout << res[i];
    cout << endl;
    
    return 0;
}

AcWing 1315. 网格

问题描述

• 问题链接：AcWing 1315. 网格

分析

• 用求卡特兰数的方法分析一下这个题目就可以得到答案。

• 我们需要求出点(n, m)关于y = x + 1对称的点的坐标，假设为(a, b)，则任何一种不合法的方案都可以转化为到达(a, b)的路径，如下图：

• 则答案为：$C_{m+n}^n-C_{m+n}^a$，问题就转变为了如何求解坐标(a, b)。这是高中知识，我们可以列方程求解，根据垂直可以得到一个等式，根据线段中点在对称轴上可以得到另一个等式，可以得到：

$$\{\begin{array}{l}1\times \frac{b-m}{a-n}=-1\\ \frac{b+m}{2}=\frac{a+n}{2}+1\end{array}$$

解方程可得：a = m - 1, b = n + 1。

• 因此答案为：

$$C_{m+n}^m-C_{m+n}^{m-1}$$

• 本题需要使用到高精度求解，如果递推的话计算量为$10000^2=1\times 10^8$，再加上高精度计算会超时，因此这里求解阶乘的方式然后带入公式求组合数，类似于AcWing 888. 求组合数 IV。

代码

• C++

#include 

using namespace std;

const int N = 100010;

int primes[N], cnt;
bool st[N];
int a[N], b[N];  // C(m+n, n)结果存储在a中, C(m+n, m-1)结果存储在b中

// 筛质数
void init(int n) {
    
    for (int i = 2; i <= n; i++) {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] * i <= n; j++) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

// 返回n中质因数p的个数
int get(int n, int p) {
    
    int s = 0;
    while (n) s += n / p, n /= p;
    return s;
}

// 高精度乘法
void mul(int r[], int &len, int x) {
    
    int t = 0;
    for (int i = 0; i < len; i++) {
        t += r[i] * x;
        r[i] = t % 10;
        t /= 10;
    }
    while (t) {
        r[len++] = t % 10;
        t /= 10;
    }
}

// 返回组合数C(x, y)，结果存储在r中, r[0]是最低位
int C(int x, int y, int r[]) {
    
    int len = 1;
    r[0] = 1;
    
    for (int i = 0; i < cnt; i++) {
        int p = primes[i];
        int s = get(x, p) - get(y, p) - get(x - y, p);
        while (s--) mul(r, len, p);
    }
    
    return len;
}

// 高精度减法
void sub(int a[], int al, int b[], int bl) {
    
    for (int i = 0, t = 0; i < al; i++) {
        a[i] -= t + b[i];
        if (a[i] < 0) a[i] += 10, t = 1;
        else t = 0;
    }
}

int main() {
    
    init(N - 1);
    
    int n, m;
    cin >> n >> m;
    
    // 求出C(m+n, m)结果存储在a中, C(m+n, m-1)结果存储在b中
    int al = C(n + m, m, a);  // al是数据a的长度
    int bl = C(n + m, m - 1, b);  // bl是数据b的长度
    
    // C(m+n, m) - C(m+n, m-1)，结果存储在a中
    sub(a, al, b, bl);
    
    int k = al - 1;
    while (!a[k]) k--;
    while (k >= 0) printf("%d", a[k--]);
    
    return 0;
}

AcWing 2641. 字符串

问题描述

• 问题链接：AcWing 2641. 字符串

分析

• 将序列中的1对应到坐标系中向右走一步，序列中的0对应到向上走一步，则转化成AcWing 1315. 网格。虽然本题不用输出精确结果，但是本题比AcWing 1315高了两个数量级。
• 因此答案是：

$$C_{m+n}^m-C_{m+n}^{m-1}$$

解法一

• 因为本题可以对20100403取模，因此不需要写高精度。由于n很大，因此求解组合数使用如下公式：

$$C_a^b=\frac{a\times (a-1)\times ...\times (a-b+1)}{1\times 2\times ...\times b}$$

• 需要预处理出来阶乘，阶乘的逆元。这里要求模数必须为质数。

解法二

• 这种解法和AcWing 130. 火车进出栈问题类似，将组合数进行质因数分解，再将所有的质因数乘起来即可。公式如下：

$$C_a^b=\frac{a!}{b!\times (a-b)!}$$

• 这里不要求模数是质数。

代码

• C++

// 解法一
// 运行时间: 2051 ms
#include 

using namespace std;

typedef long long LL;

const int N = 2000010, P = 20100403;  // 是个质数

int n, m;
int fact[N];  // 阶乘
int infact[N];  // 阶乘的逆元

int qmi(int a, int b, int p) {
    
    int res = 1;
    while (b) {
        if (b & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        b >>= 1;
    }
    return res;
}

// 返回C(a, b) % P的结果
int get(int a, int b) {

    return (LL)fact[a] * infact[b] % P * infact[a - b] % P;
}

int main() {
    
    cin >> n >> m;
    
    
    // 预处理
    fact[0] = infact[0] = 1;
    for (int i = 1; i <= n + m; i++) 
        fact[i] = (LL)fact[i - 1] * i % P;
    // 需要使用infact[n], infact[m], infact[n+1], infact[m-1]
    // 因此最大值为 n+1
    for (int i = 1; i <= n + 1; i++) 
        infact[i] = (LL)infact[i - 1] * qmi(i, P - 2, P) % P;

    
    // C(m+n, m) - C(m+n, m-1)
    int res = (get(n + m, m) - get(n + m, m - 1) + P) % P;
    
    cout << res << endl;
    
    return 0;
}

// 解法二
// 运行时间: 145 ms
#include 

using namespace std;

typedef long long LL;

const int N = 2000010, P = 20100403;

int n, m;
int primes[N], cnt;
bool st[N];

void init(int n) {
    
    for (int i = 2; i <= n; i++) {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] * i <= n; j++) {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

int get(int n, int p) {
    
    int res = 0;
    while (n) res += n / p, n /= p;
    return res;
}

int qmi(int a, int k, int p) {
    
    int res = 1 % p;
    while (k) {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a %p;
        k >>= 1;
    }
    return res;
}

int C(int a, int b, int p) {
    
    int res = 1;
    for (int i = 0; i < cnt; i++) {
        int prime = primes[i];
        int s = get(a, prime) - get(b, prime) - get(a - b, prime);
        res = (LL)res * qmi(prime, s, p) % p;
    }
    return res;
}

int main() {
    
    cin >> n >> m;
    
    init(n + m);
    
    cout << (C(n + m, m, P) - C(n + m, m - 1, P) + P) % P << endl;
    
    return 0;
}

AcWing 1316. 有趣的数列

问题描述

• 问题链接：AcWing 1316. 有趣的数列

分析

• 我们要有这种直觉：一旦发现输入是3，输出是5，很可能就是卡特兰数。

• 如何判断某个问题是不是卡特兰数呢？一般由两种方式：

  （1）能得到公式：$h(n)={\sum }_{i=1}^{n}h(i-1)\times h(n-i)h(0)=1$；

  （2）能挖掘出如下性质：任意前缀中，某种东西的数量 $\ge$ 另一种东西数量。

• 从1到2n依次考察每个元素放置的位置，1只能放在第一个位置，2只能放在第二个位置，且任意时刻我们放置的数据中奇数项的个数必须大于等于偶数项的数量。否则，假设我们奇数项放置2个元素，偶数项放置3个元素，则不合法，如下图：

• 我们可以这样对应：在从1到2n依次考察每个元素时，如果这个数据放到奇数位置，标为0，否则标为1。则任意前缀中0的个数要大于等于1的个数。
• 卡特兰数为：

$$\frac{C_{2n}^n}{n+1}$$

• 因为这里的p不一定是质数，其他数与p不一定存在逆元，因此不能使用求逆元的方法。因此这里使用卡特兰数推导的前一步公式：

$$C_{2n}^n-C_{2n}^{n-1}$$

• 组合数等于三个阶乘相乘除，因此我们求出各个阶乘的质因数分解，就能得到组合数的模p后大小。

代码

• C++

#include 

using namespace std;

typedef long long LL;

const int N = 2000010;

int n, p;  // 这里的p不一定是质数
int primes[N], cnt;
bool st[N];

void init(int n) {
    
    for (int i = 2; i <= n; i++) {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] * i <= n; j++) {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

int get(int n, int p) {
    
    int res = 0;
    while (n) res += n / p, n /= p;
    return res;
}

int qmi(int a, int k) {
    
    int res = 1 % p;
    while (k) {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a %p;
        k >>= 1;
    }
    return res;
}

int C(int a, int b) {
    
    int res = 1;
    for (int i = 0; i < cnt; i++) {
        int prime = primes[i];
        int s = get(a, prime) - get(b, prime) - get(a - b, prime);
        res = (LL)res * qmi(prime, s) % p;
    }
    return res;
}

int main() {
    
    cin >> n >> p;
    
    init(n * 2);
    
    cout << (C(n * 2, n) - C(n * 2, n - 1) + p) % p << endl;
    
    return 0;
}