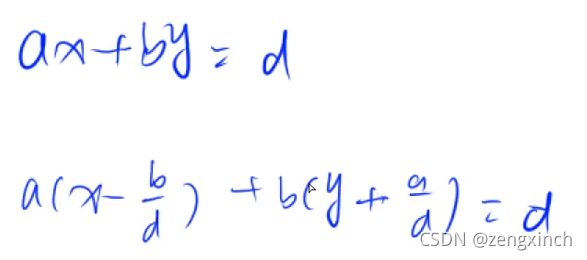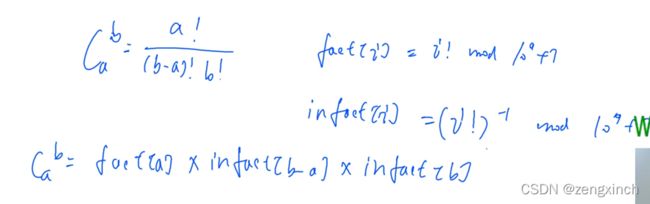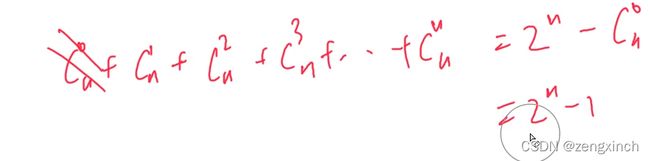AcWing 算法基础课学习记录（Python，备战蓝桥杯）Day31 - Day60

Day31.(2021.11.17)

 最小生成树，正边负边都没有关系。（

给定一张边带权的无向图G=(V,E)，其中 V 表示图中点的集合，E 表示图中边的集合，n=|V|，m=|E|。

由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。

）

 和dijkstra很像，不同的是这个是到集合的距离。

# acwing 858. Prim算法求最小生成树

null = 0x3f3f3f3f

def prim():
    dist[1], res = 0, 0
    
    for _ in range(n):
        t = -1
        for j in range(1, n + 1):
            if not st[j] and (t == -1 or dist[t] > dist[j]):
                t = j
                
        if dist[t] == null: return 'impossible'
        res, st[t] = res+dist[t], True
        for j in range(1, n + 1):
            dist[j] = min(dist[j], graph[t][j])
    return res


if __name__ == '__main__':
    n, m = map(int, input().split())
    graph, dist, st = [[null] * (n+1) for _ in range(n+1)], [null] * (n+1), [False] * (n+1)
    for i in range(1,n+1): graph[i][i] = 0
    
    for _ in range(m):
        u, v, w = map(int, input().split())
        if u==v: continue
        graph[u][v] = graph[v][u] = min(graph[u][v], w)
        
    ans = prim()
    print(ans)

#----------------------------------------------------------------------------------------

# acwing 858. Prim算法求最小生成树

N, NULL = 510, 0x3f3f3f3f

def prim():
    res = 0
    for i in range(n):
        t = -1
        for j in range(1,n+1):
            if not st[j] and (t==-1 or dist[t]>dist[j]):
                t = j
        if (i and dist[t]==NULL): return 'impossible'
        if i: res += dist[t]
        st[t] = True
        for j in range(1,n+1):
            dist[j] = min(dist[j], grid[t][j])
    return res


if __name__ == '__main__':
    grid, dist, st = [[NULL]*N for _ in range(N)], [NULL]*N,[False]*N
    n,m = map(int, input().split())
    for _ in range(m):
        u,v,w = map(int,input().split())
        grid[u][v] = grid[v][u] = min(grid[u][v], w)
    ans = prim()
    print(ans)

# acwing 858. Prim算法求最小生成树
# 感觉直接令dist[1]=0，更简洁

N, NULL = 510, 0x3f3f3f3f

def prim():
    dist[1]=0
    res = 0

    for i in range(n):
        t = -1
        for j in range(1,n+1):
            if not st[j] and (t==-1 or dist[t]>dist[j]):
                t = j
        if dist[t]==NULL: return 'impossible'
        else: res += dist[t]
        st[t] = True
        for j in range(1,n+1):
            dist[j] = min(dist[j], grid[t][j])

    return res


if __name__ == '__main__':
    grid, dist, st = [[NULL]*N for _ in range(N)], [NULL]*N, [False]*N
    n,m = map(int, input().split())
    for _ in range(m):
        u,v,w = map(int, input().split())
        grid[u][v] = grid[v][u] = min(grid[v][u], w)
    ans = prim()
    print(ans)

# acwing 859. Kruskal算法求最小生成树

N = 100010

def find(x):
    if p[x]!=x:
        p[x] = find(p[x])
    return p[x]

def kruskal():
    edges.sort(key=lambda x:x[2])

    res, cnt = 0, 0
    for i in range(m):
        a, b, w = edges[i]
        a, b = find(a), find(b)
        if a!=b:
            p[a] = b
            res += w
            cnt += 1
    if cnt<(n-1): return 'impossible'
    else: return res


if __name__ == '__main__':
    p, edges = [x for x in range(N)], []
    n,m = map(int,input().split())
    for _ in range(m):
        u,v,w = map(int,input().split())
        edges.append((u,v,w))
    ans = kruskal()
    print(ans)

八数码

# acwing 845. 八数码
# 如有有答案的话，那用宽搜肯定可以找到
# 而且是最近的那条，因为你朝所有方向走
# 那正确的那条道路肯定被包括了
# python dict底层使用hash实现的，查找键的时间复杂度是O(1)
# 这道题相比普通宽搜就是将状态记录数组转换成了状态转移查询字典

from collections import deque
from collections import defaultdict

def dfs(state):
    directions = [(1,0),(0,1),(-1,0),(0,-1)]
    end = '12345678x'

    q = deque([state])
    dist = defaultdict(int)
    dist[state] = 0

    while q:
        t = q.popleft()
        if t==end: return dist[t]
        k = t.find('x')
        x, y = k//3, k%3
        for direction in directions:
            a, b = x+direction[0], y+direction[1]
            if a>=0 and a<3 and b>=0 and b<3:
                t_list = list(t)
                t_list[3*a+b], t_list[k] = t_list[k], t_list[3*a+b]
                t_str = ''.join(t_list)
                if not dist[t_str]:
                    dist[t_str] = dist[t] + 1
                    q.append(t_str)
    return -1

if __name__ == '__main__':
    s = ''.join(input().split())
    print(dfs(s))

Day32.(2021.11.18)

二分图：当且仅当图中不包含奇数环

(划分成两个集合，集合内部没有边)

# dfs Python栈溢出，不能AC
N, M = 100010, 200010

def add(a,b):
    global idx

    e[idx] = b
    ne[idx] = h[a]
    h[a] = idx
    idx += 1

def dfs(u,c):
    color[u] = c
    i = h[u]

    while i!=-1:
        b = e[i]
        if not color[b]:
            if not dfs(b, 3-c): return False
        elif color[b] == c: return False
        i = ne[i]
    return True

if __name__ == '__main__':
    h, e, ne, idx = [-1]*N, [0]*M, [0]*M, 0
    color = [0]*N
    n, m = map(int, input().split())
    for _ in range(m):
        u, v = map(int, input().split())
        add(u,v)
        add(v,u)

    flag = True
    for i in range(1,n+1):
        if not color[i]:
            if not dfs(i,1):
                flag = False
                break
    if flag: print('Yes')
    else: print('No')

# 这道题不直接把所有点先放入q，它和844不同
# 844与上一个状态无关，这个和上一个状态有关
from collections import deque

N, M = 100010, 200010


def add(a,b):
    global idx

    e[idx] = b
    ne[idx] = h[a]
    h[a] = idx
    idx += 1


def bfs(inode):
    q = deque([inode])
    color[inode] = 1

    while q:
        t = q.popleft()
        c = color[t]
        index = h[t]
        while index!=-1:
            b = e[index]
            if not color[b]:
                color[b] = 3-c
                q.append(b)
            elif color[b]==c: return False
            index = ne[index]

    return True

if __name__ == '__main__':
    h,e,ne,idx = [-1]*N, [0]*M, [0]*M, 0
    color = [0]*N
    n, m = map(int,input().split())
    for _ in range(m):
        u, v = map(int, input().split())
        add(u,v)
        add(v,u)

    Flag = True
    for i in range(1,n):
        if not color[i]:
            if not bfs(i):
                Flag = False
                break

    if Flag: print('Yes')
    else: print('No')

Day33.(2021.11.19)

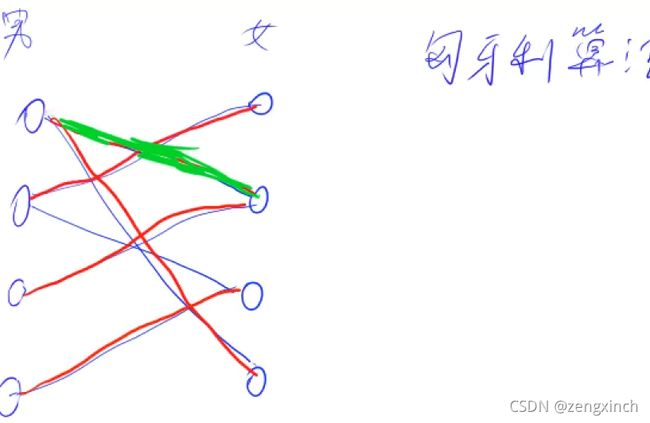
匈牙利算法

# acwing 861. 二分图的最大匹配
# 左半集合代表男生，右半集合代表女生
# match[i] = j表示女孩i的男友是j

# st表示在给i （for i 的这个循环的i）分配女朋友的这一轮中，他有好几个可能对象
# 先试试第一个女性朋友有没有男朋友或者可以抢过来不（让她的男朋友去找她男
# 朋友以前的下一个暧昧对象）
# 每个确定一定有配对的都会被赋值为True
# 每轮情况都不一样，所以每轮都要初始化一次st
N, M = 510, 100010

def add(a,b):
    global idx

    e[idx] = b
    ne[idx] = h[a]
    h[a] = idx
    idx += 1


def find(x):
    i = h[x]
    while i!=-1:
        b = e[i]
        if not st[b]:
            st[b] = True
            if match[b]==0 or find(match[b]):
                match[b] = x
                return True
        i=ne[i]
    return False

if __name__ == '__main__':
    h, e, ne, idx = [-1]*N, [0]*M, [0]*M, 0
    match, st = [0]*N, [False]*N,
    n1, n2, m = map(int, input().split())
    for _ in range(m):
        a,b = map(int, input().split())
        add(a,b)
    res = 0
    for i in range(1,n1+1):
        st = [False]*N
        if find(i): res+=1
    print(res)

Day34.(2021.11.20)

这个线性筛想了三四个小时，总算是懂了。明天再来写解答了。

# acwing 868. 筛质数
# 线性筛有个很重要的特点，就是他可以遍历1-n中的所有数，且只遍历一次

N = 1000010

def get_prime():
    global cnt

    for i in range(2,n+1):
        if not st[i]:
            cnt += 1
        # 不管是合数还是质数，都用来筛掉它的倍数
        for j in range(i,n+1,i):
            st[j] = True

def get_prime_egypt():
    global cnt

    for i in range(2,n+1):
        if not st[i]:
            cnt += 1
            # 可以用质数就把所有合数筛掉
            for j in range(i,n+1,i):
                st[j] = True

# 保证n只会被它的最小质因子筛掉（埃式筛法比如6会被2和3都筛一次）
def get_prime_linear():
    global cnt

    for i in range(2,n+1):
        if not st[i]:
            primes[cnt] = i
            cnt += 1
        
        # 内层循环判断primes[j]>n/i就break，保证primes[j]*i < n，st数组不会越界
        for j in range(cnt):
            if prime[j]>n/i: break
            st[prime[j]*i] = True
            if i%prime[j] == 0: break

if __name__ == '__main__':
    primes, cnt, st = [0]*N, 0, [False]*N
    n = int(input())
    get_prime_linear()
    print(cnt)

由于普通筛选和埃式筛都比较简单，就不过多讲解了，这里主要看线性筛。

核心思想：在埃氏筛法的基础上，让每个合数只被它的最小质因子筛选一次，以达到不重复的目的。

(1) 首先来看，合数一定会被筛掉。

假设pj（prime[j]）是x的最小质因子，当i循环到x/pj的时候，就会被筛掉。所以 i 在消去合数中的作用是当做倍数的，i 又是从2到n，肯定可以消完所有合数。

(2) 再来看为什么可以保证每个合数是用其最小质数筛掉的。

 这里引出了一个问题，为什么要在 == 0 的时候break掉， 当 i 是 prime[j] 的倍数时，i = k * prime[j] ，如果继续运算 j+1，i * prime[j+1] = prime[j] * k * prime[j+1]，这里prime[j]是最小的质因子，当 i 循环到 = k * prime[j+1] 时会和 i * prime[j+1] ，所以要跳出循环。

(3) 再来看在循环的时候不必要加上判断j < cnt:

  void get_primes(int n)
  {
      for (int i = 2; i <= n; i ++ )
      {
          if (!st[i]) primes[cnt ++ ] = i;
          // j < cnt 不必要，因为 primes[cnt - 1] = 当前最大质数
          // 如果 i 不是质数，肯定会在中间就 break 掉
          // 如果 i 是质数，那么 primes[cnt - 1] = i，也保证了 j < cnt
          for (int j = 0; primes[j] <= n / i; j ++ )
          {
              st[primes[j] * i] = true;
              if (i % primes[j] == 0) break;
          }
      }
  }

 (4) 最后来看内层 for 循环的结束条件：

 内层循环判断primes[j]>n/i就break，保证primes[j]*i < n，st数组不会越界

Day35.(2021.11.21)

1. 质数和合数是针对所有大于 1 的 “自然数” 来定义的（所有小于等于1的数都不是质数，也不是合数）。

2. 质数只能够被1和自身整除。

# acwing 866. 试除法判定质数
import math

def is_prime(x):
    # if x<2: return False
    # if x==2: return True
    # end = math.ceil(math.sqrt(x))+1
    # for i in range(2,end):
    #     if x%i == 0: return False
    # return True

    if x<2: return False
    for i in range(2,x):
        if i>x/i: break
        if x%i == 0 :return False
    return True


def is_prime(x):
    if x<2: return False
    for i in range(2,x+1):
        if i>x/i: return True
        if x%i==0: return False


if __name__ == '__main__':
    n = int(input())
    for _ in range(n):
        if is_prime(int(input())): print('Yes')
        else: print('No')

 这个第三点可以用2^3x5^2x7^3来模拟，可能会更加清晰一点。

# acwing 867. 分解质因数

def divide(x):
    for i in range(2,x):
        if i>x/i: break
        if x%i==0:
            s = 0
            while x%i == 0:
                x //= i
                s += 1
            print(i,s)
    if x>1: print(x,1)
    print()


if __name__ == '__main__':
    n = int(input())
    for _ in range(n):
        divide(int(input()))

Day36.(2021.11.22)

# AcWing 869. 试除法求约数

def get_divisor(x):
    q = []

    for i in range(1,x+1):
        if i > x/i: break
        if x%i==0:
            q.append(i)
            if i != x/i: q.append(x//i)
    q.sort()
    return q

if __name__ == '__main__':
    n = int(input())
    for _ in range(n):
        print(' '.join(map(str, get_divisor(int(input())))))

Day37.(2021.11.23)

约数个数：N可以分解为不同的质数相乘（不同质数的指数也不一样），那么每一种不同指数的选择的结果就是一个约数。所以约数的个数就是所有质数所有指数的选择情况（(α1+1) ... (αk+1)）

# acwing 870. 约数个数
from collections import defaultdict

M = 1e9+7

if __name__ == '__main__':
    primes = defaultdict(int)
    n = int(input())
    for _ in range(n):

        x = int(input())
        for i in range(2,x+1):
            if i>x/i: break
            while x%i==0:
                x //= i
                primes[i] += 1
        if x>1: primes[x] += 1

    res = 1
    for p in primes.items():
        res = res * (p[1]+1) % M

    print(int(res))


######################################

from collections import defaultdict

M = int(1e9 + 7)

def get_prime(x):
    for i in range(2,x+1):
        if i>x/i: break
        while x%i==0:
            x //= i
            primes[i] += 1
    if x>1: primes[x] += 1

if __name__ == '__main__':
    primes, ans = defaultdict(int), 1
    n = int(input())

    for _ in range(n):
        get_prime(int(input()))

    for p in primes.values():
        ans = ans * (p + 1) % M
    print(ans)

额外的知识点：int范围内整数，约数最多的为1500个左右。

1-n中倍数的个数和约数的个数相同，比如1有n个倍数，就有n个数有约数1。

# acwing 871. 约数之和
from collections import defaultdict

M = int(1e9+7)

if __name__ == '__main__':
    primes, ans = defaultdict(int), 1
    n = int(input())

    for _ in range(n):
        x = int(input())
        for i in range(2,x+1):
            if i > x/i: break
            while x%i==0:
                primes[i] += 1
                x //= i
        if x>1: primes[x] += 1

    for p in primes.items():
        a, b, t = p[0], p[1], 1
        while b:
            t = (t*a+1) % M
            b -= 1
        ans = ans * t % M

    print(ans)

欧几里得算法（辗转相除法）

d|a, d|b, 则 d|ax+by  （d能整除a...）

（a,b）= （b,a%b）          a%b = a - b*int(a/b)     int(a/b) = c

（a,b）= （b,a-c*b）          通过上面那个原理，证明这个式子可以从左边转到右边，右边转到左边，所以左右两边最大公约数相同。

0和任何数的最大公约数为任何数。

# acwing 872. 最大公约数

def gcd(a,b):
    return gcd(b,a%b) if b else a

if __name__ == '__main__':
    n = int(input())
    for _ in range(n):
        a, b = map(int, input().split())
        print(gcd(a,b))

欧拉定理：

互质是公约数只有1的两个整数，叫做互质整数。

 

 

# acwing 873. 欧拉函数

def phi(x):
    res = x
    for i in range(2,x+1):
        if i>x/i: break
        if x%i==0:
            res = res//i*(i-1)
            while x%i==0:
                x//=i
    if x>1: res = res//x*(x-1)
    return int(res)

if __name__ == '__main__':
    n = int(input())
    for _ in range(n):
        print(phi(int(input())))

# acwing 874. 筛法求欧拉函数

# 1和1互质！

# 如果 n 是个质数，那么从1~n中与它互质的数的个数为n-1 （除了它自己）
# 如果 i mod pj == 0 说明pj是i的一个质因子 （欧拉函数和质因子的次数是没有关系的）



def get_primes():
    eulers[1] = 1
    for i in range(2,n+1):
        if not st[i]:
            primes.append(i)
            eulers[i] = i-1
        for j in range(len(primes)):
            if i>n/primes[j]: break
            st[i*primes[j]] = 1
            if i%primes[j]!=0: eulers[i*primes[j]] = eulers[i]*(primes[j]-1)
            else:
                eulers[i * primes[j]] = eulers[i] * primes[j]
                break


if __name__ == '__main__':
    n = int(input())
    st, primes, eulers = [0]*(n+1), [], [0]*(n+1)
    get_primes()
    print(sum(eulers))




############################################################################

N = 1000010

def get_eulers(x):
    global cnt
    eulers[1] = 1

    for i in range(2,x+1):
        if not st[i]:
            primes[cnt] = i
            cnt += 1
            eulers[i] = i-1

        for j in range(cnt):
            if primes[j] > n/i: break
            st[primes[j]*i] = True

            if i%primes[j]==0:
                eulers[i*primes[j]] = eulers[i] * primes[j]
                break
            else:
                eulers[i*primes[j]] = eulers[i] * (primes[j]-1)



if __name__ == '__main__':
    primes, st, eulers, cnt, res = [0]*N, [False]*N, [0]*N, 0, 0
    n = int(input())
    get_eulers(n)
    for i in range(1,n+1):
        res += eulers[i]
    print(res)

Day38.(2021.11.24)

欧拉定理和费马小定理的证明

 

 

 

快速幂（反复平方法）

 

 

# acwing 875. 快速幂

def qmi(a,k,p):
    res = 1
    while k:
        if k&1: res = res*a % p
        a = a*a % p
        k = k>>1
    return res

if __name__ == '__main__':
    n = int(input())
    for _ in range(n):
        a,k,p = map(int,input().split())
        print(qmi(a,k,p))

Day39.(2021.11.26)

乘法逆元：

b⊥m，b|a
则 ∃x，使 a/b ≡ b*x (mod m)
称 x 为 b mod m 的乘法逆元

b存在乘法逆元 <=> b,m互质  （当m为质数时，b^(m-2)为b的乘法逆元）

 ​​​​​

 x = a^(p-2)，图上写错了

这里为什么可以约掉a呢，因为b和m互质，说明b和m没有共同的质因子，而a是b的倍数，若a=b*p （p是一个质数，且不为构成m的质因子）那么这个时候a肯定和m也互质，这个时候就可以约掉a了。

# acwing 876. 快速幂求逆元

def qmi(a, b, p):
    res = 1
    while b:
        if b&1: res = res*a % p
        a = a*a%p
        b = b>>1
    return res


if __name__ == '__main__':
    n = int(input())
    for _ in range(n):
        a, p = map(int, input().split())
        # 定义中要求a和p互质，但是题目没有说a和p互质，所以要检查下
        if a%p==0: print('impossible')
        else: print(qmi(a,p-2,p))

（单看下面左边那个公式）a和b都是他们自己最大公约数的倍数，因此d也要是最大公约数的倍数才行，xy才有解。

 

# acwing 877. 扩展欧几里得算法

def exgcd(a,b):
    if b==0: return 1, 0
    x1, y1 = exgcd(b, a%b)
    return y1, x1-a//b*y1

if __name__ == '__main__':
    n = int(input())
    for _ in range(n):
        a, b = map(int, input().split())
        x, y = exgcd(a,b)
        print(x,y)

裴蜀定理：任意整数x,y， ax+by 都是 gcd(a,b)的倍数，同时也存在x，y，使得ax+by=gcd(a,b)。

a，b互质 <=> ∃x,y st. ax+by=1

ax+by = 0 的一般解：

x = k*b/(a,b)
y = -k*a/(a,b)

# acwing 878. 线性同余方程

def exgcd(a,b):
    if b == 0: return a,1,0

    gcd, x1, y1 = exgcd(b,a%b)

    return gcd, y1, x1-a//b*y1

if __name__ == '__main__':
    n = int(input())
    for _ in range(n):
        a, b, m = map(int, input().split())
        gcd, x, y = exgcd(a,m)
        if b%gcd: print('impossible')
        else: print(x * (b // gcd)  % m)

中国剩余定理 

我们可以看到，右边x代入式子中，每一个都是成立的。如 mod m1，a1M1M1-1 mod m1 为a1，其它每项(a2M2M2-1...) mod m1都为0 （因为都包括m1，取模就为0）

Day40.(2021.11.28)

这道题（难度很大，对于我这种数学不好的）建议看这两个解答，讲的还是很清楚：

AcWing 204. 表达整数的奇怪方式 - AcWing

AcWing 204. 表达整数的奇怪方式 - AcWing

def exgcd(a,b):
    if b==0: return a,1,0
    gcd, x1,y1 = exgcd(b,a%b)
    return gcd, y1, x1-a//b*y1

if __name__ == '__main__':
    n = int(input())
    x = 0
    a1, m1 = map(int, input().split())

    for _ in range(n-1):
        a2, m2 = map(int, input().split())
        gcd, k1, k2 = exgcd(a1, a2)
        if (m2-m1) % gcd:
            x=-1
            break

        k1 = k1*(m2-m1)//gcd % (a2//gcd)
        x = k1*a1 + m1

        m1 = k1*a1 + m1
        a1 = a1//gcd*a2

    if x!=-1:
        x = m1%a1

    print(x)

Day40.(2021.11.29)

今天复习了约数的题。

Day41.(2021.11.30)

今天复习了欧拉函数的题。

Day42.(2021.12.1)

今天复习了快速幂、扩展欧几里得和中国剩余定理的题。

Day43.(2021.12.2)

高斯消元

用来解方程 n^3时间复杂度解n个方程n个未知数的方程组 （用了初等行列变换）

 

 

# acwing 883. 高斯消元解线性方程组

eps = 1e-6

def guass():
    r = 0
    # 对每一列开始循环
    for c in range(n):
        # 先找到当前这一列绝对值最大的数所在的行号用 t 表示。
        t = r
        for i in range(r,n):
            if abs(a[i][c]) > abs(a[t][c]): t = i
        # 当前列未定行最大的值都为0，说明所有数都是0，没有必要继续算
        if abs(a[t][c]) < eps: continue

        # 将该行换到最上面
        for i in range(c,n+1): a[t][i], a[r][i] = a[r][i], a[t][i]
        # 将该行未定数的第一个数变为 1
        for i in range(n,c-1,-1): a[r][i] /= a[r][c]

        # 将下面所有行的第 c 列变成 0
        for i in range(r+1,n):
            if abs(a[i][c]) > eps:
                for j in range(n,c-1,-1):
                    a[i][j] -= a[r][j]*a[i][c]
        r += 1

    if r eps: return 2
        return 1

    # 得到第i行的n要减去第j行的n乘以第i行第j个数
    # （乘以那么多倍，把那列数字消成0）
    # 由于第i行第i个数后面每个数都需要被消掉，所以要循环
    for i in range(n-1,-1,-1):
        for j in range(i+1,n):
            a[i][n] -= a[j][n]*a[i][j]
    return 0


if __name__ == '__main__':
    n = int(input())
    a = []
    for _ in range(n):
        a.append([float(x) for x in input().split()])
    t = guass()

    if not t:
        for i in range(n): print('{:.2f}'.format(a[i][n]))
    elif t==1: print('Infinite group solutions')
    else: print('No solution')

求组合数：

四百万的复杂度求出所有Cab的值（直接Cab要2亿）

# acwing 885. 求组合数
N, M = 2010, int(1e9+7)

def init():
    for i in range(N):
        for j in range(i+1):
            if not j: c[i][j] = 1
            else: c[i][j] = (c[i-1][j] + c[i-1][j-1]) % M


if __name__ == '__main__':
    n = int(input())
    c = [[0]*N for _ in range(N)]
    init()
    for _ in range(n):
        a, b = map(int, input().split())
        print(c[a][b])

 

 

# acwing 866. 求组合数II

N, M = 100010, int(1e9+7)

def qmi(a,k,p):
    res = 1
    while k:
        if k&1: res = res*a%p
        a = a*a%p
        k = k>>1
    return res

if __name__ == '__main__':
    fact, infact = [0]*N, [0]*N
    fact[0] = infact[0] = 1
    for i in range(1,N):
        fact[i] = fact[i-1]*i % M
        infact[i] = infact[i-1] * qmi(i,M-2,M) % M
    n = int(input())
    for _ in range(n):
        a,b = map(int, input().split())
        print(fact[a]*infact[b]%M*infact[a-b]%M)

卢卡斯定理证明

 

 

Day44.(2021.12.3)

卢卡斯定理

# acwing 887. 求组合数III

def qmi(a,k,p):
    res = 1
    while k:
        if k&1: res = res*a%p
        a = a*a%p
        k = k>>1
    return res

def C(a,b,p):
    if b>a: return 0
    res = 1
    # 这样写虽然可以过，但是模拟C76感觉就不是很对，
    # 所以还是用下面的循环
    # for i in range(a,a-b,-1):
    #     res = res*i%p*qmi(b,p-2,p)%p
    #     b -= 1

    for i in range(1,b+1):
        res = res*a*qmi(i,p-2,p)%p
        a-=1
    return res

def lucas(a,b,p):
    if a

Day45.(2021.12.4)

# acwing 888. 求组合数IV
N = 5010

def get_primes(n):
    global cnt

    for i in range(2,N):
        if st[i]:
            primes[cnt] = i
            cnt += 1

        for j in range(cnt):
            if i>n/primes[j]: break
            st[i*primes[j]] = False
            if i%primes[j] == 0: break

# 注意这个是求以n为阶乘，质数p的个数
def get(n,p):
    res = 0
    while n:
        res += n//p
        n //= p
    return res

# 这里不需要考虑b为0，所以不需要在mul的最后那里检查res[-1] == 0
def mul(A,b):
    t = 0
    res = []
    for i in range(len(A)):
        t += A[i]*b
        res.append(t%10)
        t = t//10
    while t:
        res.append(t%10)
        t //= 10
    return res


if __name__ == '__main__':
    # sum[i]是指primes[i]这个质数在阶乘的结果中指数是多少
    primes, st, cnt, sum = [0]*N, [True]*N, 0, [0]*N
    a, b = map(int, input().split())

    get_primes(a)

    for i in range(0, cnt):
        p = primes[i]
        sum[i] = get(a,p) - get(a-b,p) - get(b,p)

    res = [1]
    for i in range(cnt):
        for j in range(sum[i]):
            res = mul(res, primes[i])

    res.reverse()
    print(''.join(map(str, res)))

N = 5010

def mul(A,b):
    res, t = [], 0
    for i in range(len(A)):
        t += A[i]*b
        res.append(t%10)
        t //= 10
    while t:
        res.append(t%10)
        t //= 10
    return res

def div(A,b):
    res, i, t = [], len(A)-1, 0

    while i>=0:
        t = A[i] + t * 10
        res.append(t // b)
        t %= b
        i -= 1
    while len(res)>1 and res[0]==0:
        res.pop(0)
    return res

if __name__ == '__main__':
    a,b = map(int,input().split())
    res = [1]
    for i in range(1,b+1):
        res = div(mul(res,a),i)
        a-=1
        res.reverse()
    res.reverse()
    print(''.join(map(str,res)))

卡特兰数

# acwing 889. 满足条件的01序列

M = int(1e9+7)

def qmi(a,k,p):
    res = 1
    while k:
        if k&1: res = res*a%p
        a = a*a%p
        k = k>>1
    return res


if __name__ == '__main__':
    n = int(input())
    a, b, res = 2*n, n, 1
    for i in range(a,a-b,-1): res = res*i%M
    for i in range(1,b+1): res = res*qmi(i,M-2,M)%M
    res = res*qmi(n+1,M-2,M)%M
    print(res)

异或（不进位的加法）

# acwing 884. 高斯消元解异或线性方程组

eps = 1e-7

def guass():
    r = 0
    for c in range(n):
        t = r
        for i in range(r,n):
            if a[i][c]:
                t = i
                break
        if not a[t][c]: continue

        for i in range(c,n+1):
            a[r][i], a[t][i] = a[t][i], a[r][i]
        for i in range(r+1,n):
            if a[i][c]:
                for j in range(n,c-1,-1):
                    a[i][j] ^= a[r][j]
        r+=1

    if r

Day46.(2021.12.5)

 

# acwing 890. 能被整除的数

if __name__ == '__main__':
    n, m = map(int, input().split())
    p = [int(x) for x in input().split()]

    res = 0
    # 枚举从1 到 1111...(m个1)的每一个集合状态, (至少选中一个集合)
    for i in range(1, 1<>j)&1:
                # 乘积大于n，则n/t=0,跳出这轮循环
                if t*p[j]>n:
                    t=-1
                    break
                t *= p[j]
                # 有一个1，集合数量+1
                s += 1
        if t!=-1:
            # 选中奇数个集合, 则系数应该是1, n/t为当前这
            # 种状态的集合数量，反之则为 -1
            if s%2: res+= n//t
            else: res -= n//t
    print(res)

# acwing 891. Nim游戏

if __name__ == '__main__':
    n = int(input())
    a = [int(x) for x in input().split()]
    res = 0
    for i in range(n):
        res ^= a[i]
    if res: print('Yes')
    else: print('No')

 

# acwing 893. 集合-Nim游戏
# f 存储的是值为下标为i的节点的sg值

N, M = 110, 10010

def sg(x):
    if f[x]!=-1: return f[x]
    S = set()
    for i in range(k):
        if x>=s[i]: S.add(sg(x-s[i]))

    i = 0
    while True:
        if i not in S:
            f[x] = i
            return i
        else: i+=1


if __name__ == '__main__':
    k = int(input())
    s = [int(x) for x in input().split()]
    n = int(input())
    h, f = [int(x) for x in input().split()], [-1]*M
    res = 0
    for i in range(n):
        res ^= sg(h[i])
    if res: print('Yes')
    else: print('No')

Day47.(2021.12.6)

 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

 （奇数台阶为0的状态就包括无石子可拿的状态）

# acwing 892. 台阶Nim游戏

if __name__ == '__main__':
    n = int(input())
    s = [int(x) for x in input().split()]
    res = 0
    for i in range(n):
        if not i%2: res ^= s[i]
    if res: print('Yes')
    else: print('No')

如果有多个独立的局面的话，我们可以分别求每个局面的值，异或起来就是当前整个局面的sg的值。

# acwing 894. 拆分-Nim游戏
N = 110

def sg(x):
    if f[x]!=-1: return f[x]

    S = set()
    for i in range(x):
        for j in range(i+1):
            S.add(sg(i)^sg(j))

    i = 0
    while True:
        if i not in S:
            f[x] = i
            return i
        i+=1

if __name__ == '__main__':
    n = int(input())
    a, f = [int(x) for x in input().split()], [-1]*N
    res = 0
    for i in range(n):
        res ^= sg(a[i])
    if res: print('Yes')
    else: print('No')

动态规划

 dp代码优化一般是把dp方程或代码做优化

 集合划分的原则，不重不漏

# acwing 2. 01背包问题
N = 1010

if __name__ == '__main__':
    f = [[0]*N for _ in range(N)]
    n, m = map(int, input().split())
    v, w = [0]*N, [0]*N

    for i in range(1,n+1):
        v[i], w[i] = map(int, input().split())

    for i in range(1,n+1):
        for j in range(1,m+1):
            f[i][j] = f[i-1][j]
            if j>=v[i]: f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i])

    print(f[n][m])

# acwing 2. 01背包问题
N = 1010

if __name__ == '__main__':
    f = [0]*N
    n, m = map(int, input().split())
    v, w = [0]*N, [0]*N

    for i in range(1,n+1):
        v[i], w[i] = map(int, input().split())

    for i in range(1,n+1):
        for j in range(m,v[i]-1,-1):
            f[j] = max(f[j], f[j-v[i]] + w[i])
            
    print(f[m])

# acwing 3. 完全背包问题

N = 1010

if __name__ == '__main__':
    f, v, w = [[0]*N for _ in range(N)], [0]*N, [0]*N
    n, m = map(int, input().split())
    for i in range(1,n+1):
        v[i], w[i] = map(int,input().split())

    for i in range(1,n+1):
        for j in range(m+1):
            k = 0
            while k*v[i]<=j:
                f[i][j] = max(f[i-1][j-k*v[i]]+k*w[i], f[i][j])

                k+=1
    # 优化版本 1.1
    for i in range(1,n+1):
        for j in range(m+1):
            f[i][j] = f[i-1][j]
            if j-v[i]>=0: f[i][j] = max(f[i][j-v[i]]+w[i], f[i][j])

    # 终极版本 1.2
    # 状态转移方程的这个f[i][j-v[i]就是要第i层的，所以从前到后循环就是正确的
    for i in range(1,n+1):
        for j in range(v[i],m+1):
            f[j] = max(f[j-v[i]]+w[i], f[j])

    print(f[n][m])

Day48.(2021.12.7)

多重背包问题朴素版就可以直接用完全背包问题的思路解决，只是多添加一个判断条件k<=s[i]。

# acwing 4. 多重背包问题I

N = 110

if __name__ == '__main__':
    f, v, w, s = [[0]*N for _ in range(N)], [0]*N, [0]*N, [0]*N
    n, m = map(int, input().split())
    for i in range(1,n+1):
        v[i], w[i], s[i] = map(int,input().split())

    for i in range(1,n+1):
        for j in range(1,m+1):
            k = 0
            while k*v[i]<=j and k<= s[i]:
                f[i][j] = max(f[i][j], f[i-1][j-k*v[i]]+k*w[i])
                k+=1
    print(f[n][m])

但它不能像完全背包问题那样优化，

 

 我们知道n个当中的最大值，和最后一个值，并不能够求出前n-1个中的最大值。

判断某一个取不取可以转换成判断某一堆取不取，最终达到最优解的个数都一样。

# acwing 5.多重背包问题

N, M = 12010, 2010

if __name__ == '__main__':
    f,v,w = [0]*M, [0]*N, [0]*N
    n, m = map(int, input().split())
    cnt = 0
    for i in range(1,n+1):
        a,b,s = map(int, input().split())
        k = 1
        while k<=s:
            cnt += 1
            v[cnt] = a*k
            w[cnt] = b*k
            s -= k
            k *= 2
        if s>0:
            cnt += 1
            v[cnt] = a*s
            w[cnt] = b*s
    n = cnt

    for i in range(1,n+1):
        for j in range(m,v[i]-1,-1):
            f[j] = max(f[j], f[j-v[i]]+w[i])
    print(f[m])

# acwing 9. 分组背包问题

N = 110

if __name__ == '__main__':
    f, v, w, s = [0]*N, [[0]*N for _ in range(N)], [[0]*N for _ in range(N)], [0]*N
    n, m = map(int, input().split())
    for i in range(1,n+1):
        s[i] = int(input())
        for j in range(1,s[i]+1):
            v[i][j], w[i][j] = map(int, input().split())

    # for i in range(1,n+1):
    #     for j in range(1,m+1):
    #         # 不选的情况
    #         f[i][j] = f[i-1][j]
    #         for k in range(1,s[i]+1):
    #             if v[i][k]<=j:
    #                 f[i][j] = max(f[i][j], f[i-1][j-v[i][k]]+w[i][k])

    for i in range(1,n+1):
        for j in range(m,-1,-1):
            for k in range(1,s[i]+1):
                if v[i][k]<=j:
                    f[j] = max(f[j], f[j-v[i][k]]+w[i][k])

    print(f[m])

Day49.(2021.12.8)

 一般来说如果要用到i-1这一项，则从下标1开始初始化，否则0。

dp问题的时间复杂度一般为状态数量x转移量

N, INF = 510, int(-1e9)

if __name__ == '__main__':
    f, a = [[INF]*N for _ in range(N)], [[0] for _ in range(N)]
    n = int(input())
    for i in range(1,n+1):
        a[i] += [int(x) for x in input().split()]

    f[1][1] = a[1][1]
    for i in range(2,n+1):
        for j in range(1,i+1):
            f[i][j] = max(f[i-1][j-1], f[i-1][j]) + a[i][j]

    print(max(f[n]))

Day50.(2021.12.9)

# acwing 895. 最长上升子序列

N = 1010

if __name__ == '__main__':
    f = [1]*N
    n = int(input())
    a = [int(x) for x in input().split()]

    for i in range(n):
        for j in range(i):
            if a[j] f[i]:
                    f[i] = f[j] + 1
                    g[i] = j

    idx = f.index(max(f))
    print(max(f))
    while idx != -1:
        print(a[idx], end=' ')
        idx = g[idx]

Day51.(2021.12.10)

求数量是不能重复的，求最大值是可以有重复的上升

01这种情况的最大值是包含在f[i-1,j]中的，而f[i-1,j]又包含在f[i,j]中

# acwing 897. 最长公共子序列

N = 1010

if __name__ == '__main__':
    n, m = map(int, input().split())
    a, b = ' ' + input(), ' ' + input()
    f = [[0]*N for _ in range(N)]

    for i in range(1,n+1):
        for j in range(1,m+1):
            f[i][j] = max(f[i-1][j], f[i][j-1])
            if a[i]==b[j]: f[i][j] = max(f[i][j], f[i-1][j-1]+1)
    print(f[n][m])

 

# acwing282. 石子合并

N, INF = 310, int(1e9)

if __name__ == '__main__':
    # n = int(input())
    # s = [0] + [int(x) for x in input().split()]
    # f = [[0]*N for _ in range(N)]
    # for i in range(1,n+1):
    #     s[i] += s[i-1]
    #
    # for length in range(2,n+1):
    #     for i in range(1,n-length+2):
    #         l, r = i, i+length-1
    #         f[l][r] = INF
    #         for k in range(l,r):
    #             f[l][r] = min(f[l][r], f[l][k] + f[k+1][r] + s[r] - s[l-1])

N, INF = 310, 1e9

if __name__ == '__main__':
    f = [[INF]*N for _ in range(N)]
    n = int(input())
    w = [0] + [int(x) for x in input().split()]
    
    for i in range(1,n+1):
        w[i], f[i][i] = w[i] + w[i-1], 0
        
    for dur in range(2,n+1):
        for i in range(1,n+1):
            if i+dur-1>n: break
            l,r = i, i+dur-1
            for k in range(l,r):
                f[l][r] = min(f[l][r], f[l][k] + f[k+1][r] + w[r] - w[l-1])

    print(f[1][n])


# 记忆化搜索
# --------------------------------------------------------
def dp(x,y):
    if f[x][y]!=INF: return f[x][y]
    for k in range(x,y):
        f[x][y] = min(f[x][y], dp(x,k)+dp(k+1,y)+w[y]-w[x-1])
    return f[x][y]

if __name__ == '__main__':
    f = [[INF]*N for _ in range(N)]
    n = int(input())
    w = [0] + [int(x) for x in input().split()]
    
    for i in range(1,n+1):
        w[i], f[i][i] = w[i] + w[i-1], 0
    print(dp(1,n))

Day52.(2021.12.13)

 前面每种长度的上升子序列结尾的值最小是多少。（整个结尾的数值，应该是严格单调递增）

3 1 2 12 22 41。。。。 从第一个2起，能够接到3后面的数，一定能够接到1后面

# 验证了，二分的区间是1-n也使用这个公式
# 找到小于它（ai）的最大的一个数，然后更新它右边的值
# 等于找大于等于它的数，更新这个值，
# 如果找不到的话就他是最小的，应该替换第一个数

def binary_serach(x):
    l, r = 0, len(f)-1
    while l=x: r=mid
        else: l=mid+1
    return l

if __name__ == '__main__':
    n = int(input())
    arr = [0]+[int(x) for x in input().split()]
    f = [arr[1]]
    for i in range(2,n+1):
        if arr[i]>f[-1]: f.append(arr[i])
        else: f[binary_serach(arr[i])] = arr[i]
    print(len(f))

# acwing 896. 最长上升子序列 II
# 为了方便替换第一个数的情况，下标从1开始

N = 100010

if __name__ == '__main__':
    f, cnt = [0]*N, 1
    n = int(input())
    w = [0]+[int(x) for x in input().split()]
    f[1] = w[1]

    for i in range(2,n+1):
        if f[cnt]=w[i]:r=mid
                else: l=mid+1
            f[l] = w[i]
    print(cnt)

# acwing 896. 最长上升子序列II
# f存储当前长度为n = 1,2,3...的结尾字符最小的序列

#--------------------------------------------------
# 这个版本我也不知道为啥是对的了。。。。
N = 100010

if __name__ == '__main__':
    n = int(input())
    a, f = [int(x) for x in input().split()], [0] * N

    Len = 0
    for i in range(n):
        l, r = 0, Len
        while l=a[i]:r=mid
            else:l=mid+1
        if f[l]>=a[i]: f[l]=a[i]
        else:
            f[l+1]=a[i]
            Len += 1
    print(Len)



# -------------------------------------------------
# yxc代码版本

if __name__ == '__main__':
    n = int(input())
    a, f = [int(x) for x in input().split()], [0]*N

    Len = 0
    for i in range(n):
        l, r = 0, Len
        while l

Day53.(2021.12.14)

今天复习了下最长上升子序列，主要用了以前二分找左边界和右边界的思维来做这个题。

Day54.(2021.12.15)

 

个人理解：最后一步有四种情况增删改和不变

# acwing 902. 最短编辑距离

N = 1010

if __name__ == '__main__':
    n, a = int(input()), ' ' + input()
    m, b = int(input()), ' ' + input()
    f = [[0]*N for _ in range(N)]

    for i in range(max(n+1,m+1)):
        f[0][i] = f[i][0] = i

    for i in range(1,n+1):
        for j in range(1,m+1):
            f[i][j] = min(f[i-1][j],f[i][j-1]) + 1
            # if a[i]==b[j]: f[i][j] = min(f[i][j],f[i-1][j-1])
            # else: f[i][j] = min(f[i][j],f[i-1][j-1] + 1)
            f[i][j] = min(f[i][j], f[i - 1][j - 1] + int(a[i]!=b[j]))
    print(f[n][m])

Day55.(2021.12.16)

这y总竟然不奖励我几个ac币？

# acwing 899. 编辑距离


# acwing 899. 编辑距离

def edit_distance(a,b):
    len_a, len_b = len(a)-1, len(b)-1
    f = [[0]*(len_b+1) for _ in range(len_a+1)]

    for i in range(1,len_a+1):
        f[i][0] = i
    for i in range(1,len_b+1):
        f[0][i] = i

    for i in range(1,len_a+1):
        for j in range(1,len_b+1):
            # 最后一步变或者不变，变有三种方式
            if a[i] == b[j]: f[i][j] = f[i-1][j-1]
            else: f[i][j] = min(f[i-1][j],f[i][j-1],f[i-1][j-1]) + 1
    return f[len_a][len_b]


if __name__ == '__main__':
    a = []
    n, m = map(int, input().split())
    for _ in range(n):
        a.append(' ' + input())
    for _ in range(m):
        inp_list = input().split()
        res, s, t = 0, ' ' + inp_list[0], int(inp_list[1])
        for j in range(n):
            if edit_distance(a[j],s) <= t: res += 1
        print(res)



N = 1010

def edit_distance(a1,b1):
    n1, m1 = len(a1)-1, len(b1)-1
    f = [[0]*(m1+1) for _ in range(n1+1)]

    for i in range(n1+1):
        f[i][0] = i
    for i in range(m1+1):
        f[0][i] = i

    for i in range(1,n1+1):
        for j in range(1,m1+1):
            f[i][j] = min(f[i][j-1]+1, f[i-1][j]+1, f[i-1][j-1] + int(a1[i]!=b1[j]))
    return f[n1][m1]

if __name__ == '__main__':
    n, m = map(int, input().split())
    a = []
    for i in range(n):
        a.append(' ' + input())
    for i in range(m):
        in_li = input().split()
        res, s, t = 0, ' ' + in_li[0], int(in_li[1])
        for j in range(n):
            if edit_distance(a[j],s) <= t: res+=1
        print(res)

Day56.(2021.12.17)

计数问题

一般求某个区间的和，可以转换成前缀和问题。

 

 当x=0的时候，①如果还是000~abc-1则后面000~999会大于n，所以000变为001。

Day57.(2021.12.18)

# 求原数l到r这个范围的值是多少
# 这道题num和get的参数全是正常数字的存储顺序
# 特判1：0不能够在最高位出现
# 特判2：当x在最高位出现时，不存在情况1
# 特判3：当x=0，情况1需从001开始

def get(num, l, r):
    res = 0
    for i in range(l,r+1):
        res = res * 10 + num[i]
    return res

def count(n, x):
    if not n: return 0
    num = [int(x) for x in str(n)]
    res, n = 0, len(num)

    for i in range(n):
        if x==0 and i==0: continue
        if i>0:
            res += get(num, 0, i-1) * 10 ** (n-i-1)
            if not x: res -= 10 ** (n-i-1)
        if num[i]==x: res += get(num, i+1, n-1) + 1
        elif num[i]>x: res += 10 ** (n-i-1)

    return res

if __name__ == '__main__':
    while True:
        a, b = map(int, input().split())
        if a == b == 0: break
        if a > b: a, b = b, a
        for i in range(10):
            print(count(b, i) - count(a - 1, i), end=" ")
        print()

注意：
1.当判断x在第1位出现的次数时，不存在情况① 2.1当x=0且在分类①时，因为不能前导全0，因此得从001开始，（这一步特判即可）2.2同时0不能够在最高位出现。

# acwing 338. 计数问题

# 这个l,r是指的阿拉伯数（手写的那个，而不是存在数组中的左右）
# 求l到r这个范围的数的大小是多少

# def get(num, l, r):
#     res = 0
#     for i in range(l,r-1,-1):
#         res = res*10 + num[i]
#     return res
# 
# def count(n, x):
#     if not n: return 0
#     num = []
#     while n:
#         num.append(n%10)
#         n//=10
#     n = len(num)
# 
#     res = 0
#     for i in range(n-1-int(not x),-1,-1):
#         if ix: res += 10**i
#     return res


def get(num, l, r):
    res = 0
    for i in range(r,l-1,-1):
        res = res*10 + num[i]
    return res

def count(n,x):
    if not n: return 0
    num = []
    while n:
        num.append(n%10)
        n //= 10
    n = len(num)

    res = 0
    for i in range(n-1-int(not x),-1,-1):
        if ib: a, b = b, a
        for i in range(10):
            print(count(b,i) - count(a-1,i), end=" ")
        print()

Day58. (2021.12.19)

 主要参考这篇文章：AcWing 291. 蒙德里安的梦想 - AcWing

# acwing 291. 蒙德里安的梦想
# for i in range(1 << n)是看每列中有多少种合法的方案
# （n是每列的长度，所以总方案数是 1<>j)&1:
                    if cnt&1:
                        isValid = False
                        break
                    cnt = 0
                else: cnt+=1
            if cnt&1: isValid = False
            st[i] = isValid
        
        # 预处理 2
        # j：这一列的状态
        for j in range(1<

Day59. (2021.12.20)

参考链接：AcWing 91. 最短Hamilton路径 - AcWing 

# acwing 91. 最短Hamilton路径
# f[state][j]，state表示经过点的状态，j表示当前在哪个点
# 存储的值是路径最小总长度

N, M, INF = 20, 1<<20, 0x3f3f3f3f

if __name__ == '__main__':
    w, f = [], [[INF]*N for _ in range(M)]
    n = int(input())
    for i in range(n):
        w.append([int(x) for x in input().split()])
    #（最低位为1表示经过起点0，为0表示没有经过起点0）
    f[1][0] = 0

    for state in range(1,1<>j)&1:
                    # 怎么寻找到j的最短距离呢，看看从k能不能到j，如果能的话，检查距离是不是更短
                    for k in range(n):
                        f[state][j] = min(f[state][j], f[state^(1<>k)&1:
                            f[state][j] = min(f[state][j], f[state^(1<

Day60. (2021.12.21)

# acwing 285. 没有上司的舞会

import sys
sys.setrecursionlimit(6010)

N = 6010

def dfs(u):
    f[u][1] = happy[u]

    i = h[u]
    while i!=-1:
        j = e[i]
        dfs(j)
        f[u][1] += f[j][0]
        f[u][0] += max(f[j][0], f[j][1])
        i = ne[i]

def add(a,b):
    global idx
    e[idx], ne[idx], h[a], idx = b, h[a], idx, idx+1

if __name__ == '__main__':
    h, e, ne, idx = [-1]*N, [0]*N, [0]*N, 0
    happy, f, has_fa = [0]*N, [[0]*2 for _ in range(N)], [False]*N
    n = int(input())

    for i in range(1,n+1):
        happy[i] = int(input())
    for i in range(n-1):
        a, b = map(int, input().split())
        add(b,a)
        has_fa[a] = True

    root = 1
    while has_fa[root]: root+=1
    dfs(root)
    print(max(f[root][0], f[root][1]))

另一种做法：可以防止递归爆栈 AcWing 285. python3非递归解法，防止爆栈 - AcWing