集成学习-波士顿房价预测
关于集成学习算法
-
集成算法基本算法主要分为Bagging算法与Boosting算法
-
Bagging的算法过程
- 从原始样本集中(有放回的)随机抽取n个训练样本，共进行k轮抽取，得到k个训练集(k个训练集之间相互独立，元素可以有重复)
- 对于k个训练集，训练k个模型(学习器)
- 对于分类问题：由投票表决产生的分类结果；对于回归问题，由k个学习器预测结果的均值作为最后预测的结果
- 所有学习器的重要性相同
-
Boosting的算法过程（三个臭皮匠顶个诸葛亮）
- 使用所有训练样本，训练第一个弱学习器，并记录所有样本的结果(分类正确/错误，或者误差)
- 对于训练集中的每个样本建立权值，分类错误或误差较大的样本，其权重也较大；否则权重减小
- 使用相同的训练样本(不同的样本权重)，再次训练新的弱学习器；并根据预测结果继续调整样本权重
- 最终得到个弱学习器。加大误差较小的弱学习器的权值，使其在表决中起到更大的作用，减小误差较大的弱学习器的权值，使其在表决中起到较小的作用
- 根据弱学习器及其权值，形成线性组合，将组合运算的结果作为最终预测结果。（这里的权重可以应用梯度下降解决）
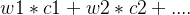;wi权重ci预测结果，如何求解,可以应用梯度下降
-
Bagging和Boosting 的主要区别
- 样本选择: Bagging采取随机有放回的取样，Boosting每一轮训练的样本是固定的，改变的是每个样本的权重
- 样本权重：Bagging采取的是均匀取样，每个样本的权重相同，Boosting根据误差调整样本权重，误差越大的样本权重越大
- 预测函数：Bagging所有的学习器权值相同，Boosting中误差较小的学习器权值也越大。
- 并行计算：Bagging 的各个学习器可以并行生成，Boosting的各个学习器必须按照顺序迭代生成
- Bagging里每个分类模型都是强分类器，目的往往是减少模型的Variance(方差)，防止过拟合；Boosting里每个分类模型都是弱分类器，目的是减少模型的Bias(偏度)，解决欠拟合问题
-
典型集成学习算法
- Bagging + 决策树 = 随机森林
- AdaBoost + 决策树 = 提升树 Boosting
- Gradient + 决策树 = GBDT(梯度提升决策树)
本演练针对波士顿房价数据集进行建模和预测。将使用多种模型，包括：线性回归、Adaboost、随机森林、GBDT、XGBoost、LightGBM。
波士顿房价数据集位于【boston_house.csv】, 一共506条数据，每条数据包括14个字段：
- 前13个字段作为特征字段
- CRIM：城镇人均犯罪率。
- ZN：住宅用地超过25000平方英尺的比例。
- INDUS：城镇非零售商用土地的比例。
- CHAS：查理斯河空变量（如果边界是河流，则为1；否则为0）。
- NOX：一氧化氮浓度。
- RM：住宅平均房间数。
- AGE：1940 年之前建成的自用房屋比例。
- DIS：到波士顿五个中心区域的加权距离。
- RAD：辐射性公路的接近指数。
- TAX：每 10000 美元的全值财产税率。
- PTRATIO：城镇学生数：教师数的比例。
- B：1000（Bk-0.63）^ 2，其中 Bk 指代城镇中黑人的比例。
- LSTAT：人口中地位低下者的比例。
- 第14个字段(MEDV，即平均房价)作为结果字段，以千美元计。
- 按照8:2的比列拆分训练数据集和测试数据集。
链接：https://pan.baidu.com/s/1uuVxPq40281V_3R-i2zwKw?pwd=6688
提取码：6688import pandas as pd
import numpy as nnp
#import pandas as pd
from sklearn.model_selection import train_test_split
data_path = './boston_house.csv'
data = pd.read_csv(data_path)
print(data.head())
X = data.iloc[:, :-1] # 前13列作为特征数据集
y = data.iloc[:, -1] # 最后1列作为结果列，
# 按照8:2拆分训练集和测试集
random_state = 100 #设置随机数种子
test_ratio = 0.2
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=test_ratio, random_state=random_state)
print("训练数据集维度：", X_train.shape)
print("测试数据集维度：", X_test.shape)
一、线性回归
1. 直接进行线性回归建模，并计算平均误差
- 误差一般采用误差平方和的平均值(MSE)，也就是使用模型预测各个测试样本的输出结果，将预测结果与实际结果对比，计算误差的平方和，再取平均值
- sklearn.metrics.mean_squared_error用于根据给定的预测值和真实值，计算MSE
from sklearn.metrics import mean_squared_error #MSE
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
# 针对测试数据集，计算误差平方和的平均值(MSE)
error = mean_squared_error(y_true=y_test, y_pred=y_pred)
print("测试数据集误差:", error)
2. 先对特征进行归一化处理，再建模
- 归一化处理时，先针对训练数据集进行归一化
- 测试数据集同样需要归一化，而且其均值和标准差应使用训练数据集的
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train_norm = scaler.transform(X_train)
X_test_norm = scaler.transform(X_test) # 使用训练数据集的均值和标准差对测试数据集进行归一化
print(X_train_norm[:5]) # 打印前5行归一化结果
model = LinearRegression()
model.fit(X_train_norm, y_train)
y_pred = model.predict(X_test_norm)
# y_pred = y_scaler.inverse_transform(y_pred)
# 针对测试数据集，计算误差平方和的平均值(MSE)
error = mean_squared_error(y_true=y_test, y_pred=y_pred)
print("测试数据集误差:", error)
二、使用随机森林
- 随机森林是典型性的基于Bagging策略的算法
- sklearn.ensemble.RandomForestRegressor提供了随机森林回归模型的实现
- n_estimators指定决策树的棵树，默认为100
- criterion指定误差计算方法，mse表示均方差，msa表示平均绝对误差
- max_depth指定决策树的最大深度
- max_samples为浮点数时，指定每棵决策树参与训练的样本占总训练样本的比例
- 此种方式误差约为10.7，效果较好
from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor(random_state=random_state)
model.fit(X_train_norm, y_train)
y_pred = model.predict(X_test_norm)
error = mean_squared_error(y_true=y_test, y_pred=y_pred)
print("测试数据集误差:", error)
三、使用AdaBoost(Adaptive Boosting)算法
- 数据权重的调整
- AdaBoost在每轮迭代中会在训练集上产生一个新的学习器，然后使用该学习器对所有样本进行预测，以评估每个样本的重要性(Informative)
- 算法为每个样本赋予一个权重，每次用训练好的学习器标注/预测各个样本。如果某个样本点被预测的越正确，则将其权重降低；否则提高样本的权重。权重越高的样本在下一个迭代训练中所占的比重就 越大，也就是说越难区分的样本在训练过程中会变得越重要。
- 整个迭代过程直到错误率足够小或者达到一定的迭代次数为止。
- 学习器的权重调整
- 在训练了多个学习器后，AdaBoost算法将学习器的线性组合作为强学习器
- 给误差率较小的学习器以大的权值，给分类误差率较大的学习器以小的权重值
- 最终这些学习器集合起来，构成一个更强的最终学习器
- 对于分类任务，学习器为分类器，例如线性分类器、决策树分类器等；对于回归任务，学习器为回归判别式。本例为回归任务。
- 学习器有多种，此处分别使用线性SVM回归判别式和决策树回归判别式两种
- sklearn.ensemble.AdaBoostRegressor提供了Adaboost回归算法实现
- base_estimator指定学习器的类型
- n_estimators指定弱学习器的个数。默认为50个
- loss指定计算误差的方式。square表示采用均方误差
1. 基于线性SVM学习器的实现
- sklearn.svm.LinearSVR提供了线性SVM回归判别式的实现
- 可以看到此种方式的误差在58.94左右，效果很不好
from sklearn.ensemble import AdaBoostRegressor
from sklearn.svm import LinearSVR # 线性支持向量回归器
estimator = LinearSVR()
model = AdaBoostRegressor(base_estimator=estimator, loss='square', random_state=random_state)
model.fit(X_train_norm, y_train)
y_pred = model.predict(X_test_norm)
error = mean_squared_error(y_true=y_test, y_pred=y_pred)
print("测试数据集误差:", error)
2. 基于决策树学习器的实现(提升树)
- sklearn.tree.DecisionTreeRegressor提供了决策树基学习器的实现
- 每一次进行回归树生成时采用的新训练数据的y值，是上次预测结果与训练数据值之间的残差。对于使用平方误差损失函数和指数损失函数时，这个残差的计算比较简单；但如果使用一般损失函数，则不易求解残差
- 此种方式的误差约9.2，效果较好
from sklearn.tree import DecisionTreeRegressor
estimator = DecisionTreeRegressor()
model = AdaBoostRegressor(base_estimator=estimator, loss='square', random_state=random_state)
model.fit(X_train_norm, y_train)
y_pred = model.predict(X_test_norm)
error = mean_squared_error(y_true=y_test, y_pred=y_pred)
print("测试数据集误差:", error)
四、GBDT(Gradient Boosting Decision Tree)梯度提升决策树算法
- 主要是为解决损失函数不是平方损失，导致不方便优化的问题
- GBDT利用损失函数的负梯度作为提升树算法中残差的近似值，这是与提升树的主要区别
- 要求弱学习器必须是基于CART模型的决策树
- 此种方式误差约为8.9，效果非常好
from sklearn.ensemble import GradientBoostingRegressor
model = GradientBoostingRegressor(random_state=random_state)
model.fit(X_train_norm, y_train)
y_pred = model.predict(X_test_norm)
error = mean_squared_error(y_true=y_test, y_pred=y_pred)
print("测试数据集误差:", error)
五、XGBoost(eXtreme Gradient Boosting)算法
- 与GBDT相比，不仅支持CART决策树，也支持线性分类器
- 目标函数中引入了正则项，便于降低模型方差，防止过拟合
- 对缺失值不敏感，能自动学习其分裂方向
- 需要预先安装xgboost包(pip install xgboost)
#!pip install xgboost #安装xgboost
#!conda install xgboost from xgboost import XGBRegressor
random_state = 100
model = XGBRegressor(random_state=random_state)
model.fit(X_train_norm, y_train)
y_pred = model.predict(X_test_norm)
error = mean_squared_error(y_true=y_test, y_pred=y_pred)
print("测试数据集误差:", error)
六、LightGBM
- 与XGBoost相比，计算量减小，精度较高
- 需要预先安装lightgbm包(pip3 install lightgbm)
import lightgbm as lgb
train_set = lgb.Dataset(X_train_norm, label=y_train)
model = lgb.train(
params={
'boosting_type': 'gbdt',
'objective': 'regression'
},
train_set=train_set)
y_pred = model.predict(X_test_norm)
error = mean_squared_error(y_true=y_test, y_pred=y_pred)
print("测试数据集误差:", error)
七、选择特征
- 使用特征递归消除法(RFE)来遴选特征子集
- 选中的特征名称: Index([‘NOX’, ‘RM’, ‘DIS’, ‘TAX’, ‘PTRATIO’, ‘LSTAT’], dtype=‘object’)
- 测试数据集误差: 10.122283937555844
- 此处直接使用带交叉验证的RFE方法RFECV
- 但是从结果来看，效果还可以
import numpy as np
from sklearn.feature_selection import RFECV
from sklearn.tree import DecisionTreeRegressor
random_state = 100
estimator = DecisionTreeRegressor(random_state=random_state)
rfecv = RFECV(estimator=estimator, step=1, cv=5)
rfecv.fit(X_train_norm, y_train)
print("选中的特征名称: " , X_train.columns[rfecv.support_])
X_train_rfecv = rfecv.transform(X_train_norm)
X_test_rfecv = rfecv.transform(X_test_norm)
from sklearn.ensemble import GradientBoostingRegressor
model = GradientBoostingRegressor(random_state=random_state)
model.fit(X_train_rfecv, y_train)
y_pred = model.predict(X_test_rfecv)
error = mean_squared_error(y_true=y_test, y_pred=y_pred)
print("测试数据集误差:", error)