大数据因果推理与学习入门综合概述
在《原因与结果经济学》的开篇,给读者回答以下几个问题。
- 定期接受代谢综合征体检就能长寿吗?
- 看电视会导致孩子学习能力下降吗?
- 上录取分数高的大学收入就会更高吗?想必很多人的回答都是肯定的。
不过,经济学的权威研究已经推翻了上述全部说法。
1. 理解“因果推理”,便可摆脱传统观念的束缚
两个事件之间是否真的存在因果关系?为解答这一问题,近年来经济学研究倾注了巨大的心血。我们把正确区分因果关系和相关关系的方法论称为“因果推理”。
“因果”,顾名思义,即“原因与结果”。“推理”则指“根据某个事件推导其他事件,即经过推测和推断得出结论的过程”。换句话说,就是分析并判断两个事件是否分别为原因和结果的过程。
1.1. 因果关系与相关关系的概念
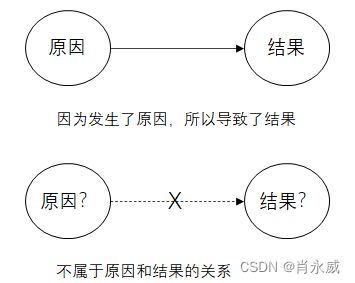
因果关系:如过两个事件中,前一个事件是后一个事件的原因,后一个事件是前一个事件的结果,则两个事件之间存在因果关系。
相关关系:如过一个事件变化后,另一个事件也随之变化,但二者不属于原因和结果的关系,则称他们之间存在相关关系。
存在相关关系的两个事件之间虽然有关联,但不属于因果关系。
1.2. 判断因果的三个要点
(1)是否“纯属巧合”?
(2)是否存在“第三变量”?术语说就是“混杂因素”。
(3)是否存在“逆向因果关系”?
如过两个变量之间存在因果关系,当原因再次出现时,相同的结果也会出现,而不是“纯属巧合”、“混杂因素(第三变量)”或“逆向因果关系”。另一方面,如过两个变量的关系只是相关关系,那么就会存在“纯属巧合”、“混杂因素”或“逆向因果关系”中的某一种情况。在相关关系的情况下,即使原因再次发生,也几乎不会得到相同的结果。
1.3. 证明因果关系需要“反事实”
没有时光机、也没有平行宇宙,就制造不出反事实吗?
克服“因果推理中的根本问题”,制造反事实,才正是以因果推理为基础的各种方法的根本所在。
例如:假设你想了解广告能为销售额带来多大的因果效应。广告的因果效应等于投放广告后的事实销售额和相同情况下没有投放广告的反事实销售额的差。主要方法有:
- 随机对照实验
- 自然实验与准实验
- 回归分析
1.4. 因果性和相关性的区别
举个例子:如果我们发现,夏天的时候,一个冰淇淋店的电费上涨的同时冰淇淋卖的也很好,我们可以说他们互相之间有因果的关系吗?不见得,他们之间可能只是统计上的相关性,而真正给他们带来的因果性的因子叫做气温,是因为气温的上升,导致电费的增加,也是因为气温的上升,导致了冰淇淋销量的上升。这个例子很好的向我们阐述了因果性和统计相关性的区别。
2. 因果革命:改变数据科学的新革命
随着机器学习建模越来越多的应用,企业对人工智能的要求也在进一步提高。近几年提及的「数智化」核心是智能决策,以数据驱动的方式实现自动化决策来提高整体运营效率。用户的需求的重心从预测性分析向指导性分析升级转移,预测性分析是告诉企业未来可能会发生什么,指导性分析也叫处方性分析,是告诉企业我们如果想要实现一个目标需要如何做,这是典型的智能决策问题。
机器学习主要用在预测性分析上,基本上没有能力解决指导性分析这样的决策问题,因此,因果学习正被学界和业界逐渐重视起来,其可以补充机器学习的一些短板,也满足了智能决策这类问题的需求。因果推断的重要性逐渐显示,被认为是人工智能领域的一次范式革命。
图灵奖得主、贝叶斯网络奠基人Judea Pearl说:”因果革命“是一场正在改变数据科学的新革命 — 。因果革命和以数据为中心的第一次数据科学革命,也就是大数据革命(涉及机器学习,深度学习机器应用,例如Alpha-Go、语音识别、机器翻译、自动驾驶等等 )的不同之处在于,它以科学为中心,涉及从数据到政策、可解释性、机制的泛化,再到一些社会科学中的基础概念信用、责备和公平性, 甚至哲学中的创造性和自由意志 。可以说, 因果革命彻底改变了科学家处理因果问题的方式。
例如,“锻炼身体是否能够有利于健康?”见下图,x轴表示运动时间,y轴表示胆固醇水平。
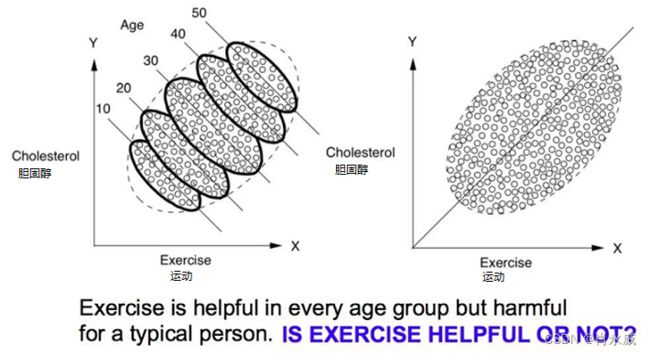
在上图(左)中,可以看大每个年龄组中都出现了向下的趋势,表明运动可能的确有降低人体胆固醇水平的效果;另一方面,在上图(右)中,同样的散点图并不依据年龄对数据进行分层,那么我们就会看到一个明显向上的趋势,这表明运动得越多,人体胆固醇水平就越高,这种矛盾在统计学中被成为辛普森悖论。
这个例子说明了数据可能对你讲出两个不同的故事。如果信息发生了一些变化,得到的结论就可能是不一样的。更加准确地来说,这个例子本质上是要回答因果问题,仅有数据信息而没有先验因果关系信息的时候,就可能得出与关注研究的问题相互矛盾的答案。回答因果问题需要因果信息。
Pearl 描述了一个因果推理的三级结构,把因果信息按其能够回答的类型进行分类。
第一层是关联(Association),它涉及由数据定义的统计相关性。大多数机器学习系统围绕这一层运行。
第二层是干预(Intervention),不仅涉及到能看到什么,还涉及一个干预或行动将会导致什么结果。作为例子,Pearl 提了一个问题:“如果我们把价格翻倍,将会发生什么?”
第三层是反事实(Counterfactual),是对以前发生的事情的反思和溯因,解决的是“如果过去作出不一样的行为,现在的结果会有何不同?”的问题。
因果革命中,数据科学的任务被重新分成了三类:预测、描述和反事实预测。
3. 因果推断入门
3.1. 因果推断研究的两个问题——从辛普森悖论讲起
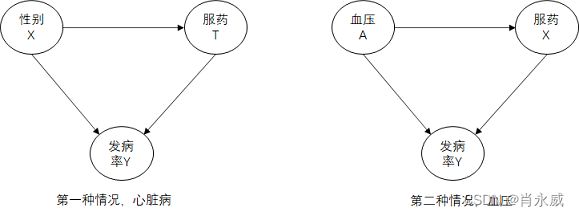
- 第一个情况,对于心脏病,男女分别来看。
| 性别 | 未服药发病 | 未服药未发病 | 未服药发病率 | 服药发病 | 服药未发病 | 服药发病率 |
|---|---|---|---|---|---|---|
| 女性 | 1 | 19 | 5% | 3 | 37 | 7.5% |
| 男性 | 12 | 28 | 30% | 8 | 12 | 40% |
| 总体 | 13 | 47 | 21.6% | 11 | 49 | 18.3% |
这个药对人类有效,发生了什么?
- 第二个情况,分血压来看。
| 性别 | 未服药发病 | 未服药未发病 | 未服药发病率 | 服药发病 | 服药未发病 | 服药发病率 |
|---|---|---|---|---|---|---|
| 血压降低 | 1 | 19 | 5% | 3 | 37 | 7.5% |
| 血压升高 | 12 | 28 | 30% | 8 | 12 | 40% |
| 总体 | 13 | 47 | 21.6% | 11 | 49 | 18.3% |
这个药对人类有效,发生了什么?
在第一个情况下,不同的性别有不同的服药意愿,也就是性别是服药和发病的共同原因,所以应该分层进行统计
在第二个情况下,服药会导致血压变化,也就是血压是服药和发病的共同结果,如果分层统计,则会低估服药的影响,总体的结论才是正确的。
从这两个辛普森悖论的例子我们可以看出现在因果推断最重要的两个研究方向:
- causal discovery:因果发现,也就是发现以上统计变量之间的因果关系,从统计变量中探寻出一个如上的因果图;
- causal effect:因果效应,在得到因果关系之后,确定效果,比如上面的问题是,知道因果图之后,确定服药之后发病率增加(减少)多少。
3.2. 常用评估指标与基本概念
3.2.1. 常用评估指标与变量定义
以第一种情况,“女性”心脏病患者服用心脏病药物为例来说明:
| 效果 | W=0(未服药) | W=1(服药/干预) |
|---|---|---|
| 未发病Y(=1) | 19 | 37 |
| 发病Y(=0) | 1 | 3 |
Y 1 ( W = 0 ) = 19 Y_1(W=0)=19 Y1(W=0)=19
Y 1 ( W = 1 ) = 37 Y_1(W=1)=37 Y1(W=1)=37
Y 0 ( W = 0 ) = 1 Y_0(W=0)=1 Y0(W=0)=1
Y 0 ( W = 1 ) = 3 Y_0(W=1)=3 Y0(W=1)=3
- Unit —— 单元,原子研究对象
- Treatment —— 干预/治疗,施加给一个原子对象unit的行为。在二元Treatment的情况下(即W=0 或 1 ),Treatment组包含接受Treatment为 W=1 的unit,而对照组包含接受Treatment为 W=0 的unit。
例如,第一种情况服药T,干预可以是一项政策、一项措施或者一项活动等。
- Outcome —— 结果,在对unit进行Treatment或者仅仅作为对照之后unit随后产生的反应/结果,一般用 Y 表示
例如,第一种情况发病率Y。
-
Treatment Effect —— 因果效应,对unit进行不同Treatment之后unit产生的Outcome的变化,这种效应可以定义在整体层面、treatment组层面、子组层面和个体层面
-
整体层面 —— Average Treatment Effect(ATE),平均干预效果
A T E = E [ Y ( W = 1 ) − Y ( W = 0 ) ] ATE = E[Y(W=1)-Y(W=0)] ATE=E[Y(W=1)−Y(W=0)]
A T E = ( Y 1 ( W = 1 ) − Y 1 ( W = 0 ) ) / ( Y 1 ( W = 1 ) + Y 1 ( W = 0 ) ) = ( 37 − 19 ) / 36 = 50 % ATE=(Y_1(W=1) - Y_1(W=0))/(Y_1(W=1) + Y_1(W=0))=(37-19)/36=50\% ATE=(Y1(W=1)−Y1(W=0))/(Y1(W=1)+Y1(W=0))=(37−19)/36=50%
- Treatment组层面 —— Average Treatment Effect on the Treated Group (ATT),Treatment组中的平均干预效果
A T T = E [ Y ( W = 1 ) ∣ W = 1 ] − E [ Y ( W = 0 ) ∣ W = 1 ] ATT=E[Y(W=1)∣W=1]−E[Y(W=0)∣W=1] ATT=E[Y(W=1)∣W=1]−E[Y(W=0)∣W=1]
A T E = ( Y 1 ( W = 1 ) − Y 0 ( W = 1 ) ) / ( Y 1 ( W = 1 ) + Y 0 ( W = 1 ) ) = ( 37 − 3 ) / 40 = 85 % ATE=(Y_1(W=1) - Y_0(W=1))/(Y_1(W=1) + Y_0(W=1))=(37-3)/40=85\% ATE=(Y1(W=1)−Y0(W=1))/(Y1(W=1)+Y0(W=1))=(37−3)/40=85%
服药干预组中,平均干预效果为85%。
-
子组层面 —— Conditional Average Treatment Effect (CATE)
C A T E = E [ Y ( W = 1 ) ∣ X = x ] − E [ Y ( W = 0 ) ∣ X = x ] CATE=E[Y(W=1)∣X=x]−E[Y(W=0)∣X=x] CATE=E[Y(W=1)∣X=x]−E[Y(W=0)∣X=x] -
个体层面 —— Individual Treatment Effect (ITE)
I T E i = E [ Y i ( W = 1 ) − Y i ( W = 0 ) ] ITE_i = E[Y_i(W=1)-Y_i(W=0)] ITEi=E[Yi(W=1)−Yi(W=0)] -
Potential Outcome —— 潜在结果,对于每对unit-treatment,当对unit施加相应的treatment之后产生的结果
潜在结果
一个或多个处理作用(干预T)在个体上产生的预期效果我们称之为潜在结果 (Potential outcome)。之所以称为潜在结果是因为在一个个体上最终只有一个结果会出现并被观察到,也就是和个体所接受的处理相对应的那个结果。另外的潜在结果是观察不到的,因为它们所对应的处理并没有实际作用在该个体上。
-
Observed Outcome —— 观测结果,已经发生的事实,对unit施加某个treatment之后产生的能观测到的结果
-
Counterfactual Outcome —— 反事实结果, 已经发生事实的其他对立面,也即对某个unit未采用的其他treatment带来的潜在结果。
-
不可见的反事实空间(Counterfactual)
对于特定个体的特定状态,我们只能对其进行一次操作(比如用药)然后观察效果,而无法获知进行相对应操作(比如服用安慰剂或不用药)下的效果。而这种无法获知的状态就称为“Counterfactual”。如果我们能够既知道real world又知道counterfactual world的情况,那么二者做差即可得到causal effect。但很遗憾counterfactual永远不可知。 -
混淆变量(Confounding Factor OR Covariates)
Treatment变量T和effect变量Y可能会同时受到某一第三方变量X的影响,导致观察到的T对Y的影响其实并不一定是真实的作用关系。比如要研究某种药对病人的效果,但研究过程中忽略了年龄的因素,结果治疗组和对照组治疗效果上的差别实际是病人年龄差异导致的,这种情况下年龄就称为混淆变量。 -
Conditional Independent Assumption(CIA) 条件独立假设问题
这里的独立是概率论意义下的独立,即A、B独立,则 P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B),不独立情况下是 P ( A B ) = P ( A ∣ B ) P ( B ) P(AB)=P(A|B)P(B) P(AB)=P(A∣B)P(B)。
3.2.2. 因果模型概述
鲁宾因果模型 Rubin Causal Model(RCM)
鲁宾因果模型 Rubin Causal Model (RCM) ,也称为 Neyman-Rubin 因果模型,是一种基于潜在结果框架的因果统计分析方法,框架有三个基本构成要件:潜在结果、稳定性假设和分配机制。
鲁宾因果模型是基于潜在结果的想法。例如,如果一个人上过大学,他在 40 岁时会有特定的收入,而如果他没有上过大学,他在 40 岁时会有不同的收入。为了衡量这个人上大学的因果效应,我们需要比较同一个人在两种不同的未来中的结果。由于不可能同时看到两种潜在结果,因此总是缺少其中一种潜在结果。这种困境就是“因果推理的基本问题”。
由于因果推理的根本问题,无法直接观察到单元级别的因果效应。然而,随机实验允许估计人口水平的因果效应。随机实验将人们随机分配到对照组:大学或非大学。由于这种随机分配,各组(平均)相等,40 岁时的收入差异可归因于大学分配,因为这是各组之间的唯一差异。然后可以通过计算处理(上大学)和对照(非上大学)样本之间的平均值差异来获得平均因果效应(也称为平均处理效应)的估计值。
潜在结果框架的第三个要件是分配机制。分配机制是描述为什么有的人在干预组,有的人在控制组,或者分配机制是描述哪个潜在结果可以被观测到的机制。因果推断中分配机制非常重要,对分配机制的了解有助于进行正确的因果推断。
结构因果模型 Structural Causal Model(SCM)
结构因果模型(SCM)结合了图形建模、结构方程、反事实和介入逻辑。
结构因果模型(SCM)是由内生变量 V V V、外生变量 U U U和映射函数 F F F构成。因果的定义:若 Y Y Y在 f X f_X fX 的定义域中,则 Y Y Y是 X X X的直接原因 ;如果 Y Y Y是 X X X的直接原因,或者是直接原因的原因,则 Y Y Y是 X X X的原因。
U U U中的变量称为外生变量,它们属于模型的外部,不必解释它们变化的原因。 V V V中的变量称为内生变量,模型中每一个内生变量都至少是一个外生变量的后代。外生变量没有祖先节点,不是内生变量的后代。
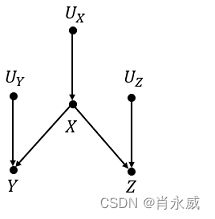
V = { X , Y , Z } , U = { U X , U Y , U Z } , F = { f X , f Y , f Z } V=\{X,Y,Z\},U=\{U_X,U_Y,U_Z\},F=\{f_X,f_Y,f_Z\} V={X,Y,Z},U={UX,UY,UZ},F={fX,fY,fZ}
f X : X = U X f_X:X=U_X fX:X=UX
f Y : Y = a x + U Y f_Y:Y=ax+U_Y fY:Y=ax+UY
f Z : Z = b x + U Z f_Z:Z=bx+U_Z fZ:Z=bx+UZ
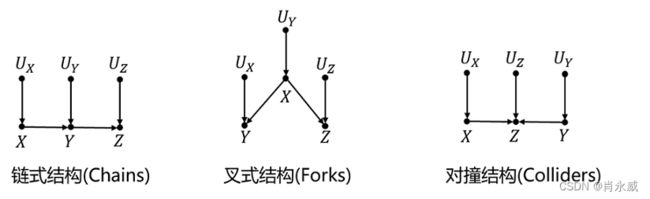
因果图的三种结构
-
链式结构,例如:火灾→烟雾→ 烟雾警报,在统计的数据中查看“烟雾=1”的数据会发现,无论是否有火灾,一定会响警报,与火灾的值为0或者1无关,以中介为条件的情况下,火灾和烟雾警报独立。
-
叉式结构,例如:鞋子尺码←年龄→阅读能力,小孩年龄大,一般鞋码长,阅读能力也更强,但是只看统计数据中“年龄=8岁”小孩的记录会发现,鞋子尺码和其阅读能力间是没有关系的。
-
对撞结构,例如:绩点→奖学金←活动分,查看获得奖学金的这些人,如果学习成绩不好,那么他们一定参加了很多活动才评上奖学金,参加活动和学习成绩产生了关联。
3.3. 因果推断与学习过程
因果推断与学习过程以鲁宾因果模型为主概述。
3.3.1. 关于因果推断研究内容
因果推断要做的是识别因果关系,量化因果作用。
因果推断两种研究方法:
- 实验性研究 —— 需要做大量随机对照试验,实验中的控制变量也是随机指定的,但这么做往往会涉及到伦理的问题。例如,当我们要研究吸烟对肺部健康的影响时,我们不可能要求原本都不吸烟的一群人中的一部分人去吸烟已到达实验目的,这是不现实且反道德及伦理的。此外,进行大量的随机对照试验代价昂贵且费时费力。
- 观测性研究 —— 从已有的能观测到的数据中进行因果关系的研究。主要方法有因果图模型和潜在结果框架。观测性研究的好处在于,简单高效且易于理解。
因果推断的三个假设:
-
假设1:稳定单位干预值假设(Stable Unit Treatment Value Assumption)
任何一个单元的潜在结果不会因分配给其他单元的treatment而有所不同,并且对于每个单元,每个treatment级别没有不同的形式或版本,不会导致不同的潜在结果。
这个假设强调以下几点:
– unit之间都是相互独立的,unit之间不会存在相互作用
– 同一treatment仅能存在一个版本。例如,在该假设下,不同剂量的同一种药物代表不同的治疗方法 -
假设2:可忽略性假设(Ignorability)
给定背景变量 X , 干预分配 W 与潜在的结果无关。
例如,由上文的药物治疗的例子来看,如果两个患者有相同的背景变量 X ,无论治疗任务是什么,他们的潜在结果应该是相同的。
类似地,如果两个患者具有相同的背景变量值,那么他们的治疗分配机制应该是相同的,无论他们有什么潜在的结果。 -
假设3:正值假设(Positivity)
对于X的任何一组值,处理分配不是确定的: P ( W = w ∣ X = x ) > 0 P(W=w∣X=x)>0 P(W=w∣X=x)>0
如果某些X值的治疗分配是确定的,那么至少一种治疗的结果永远无法观察到。那么估计因果关系是不可能也没有意义的,这意味着干预组和对照组的“共同支持”或“重叠”。忽略性和积极性假设一起也被称为强可忽略性或强可忽略性治疗任务
3.3.2. 因果推断与学习过程
因果推断与学习过程包括如下五个方面任务:
一是因果发现。利用对数据的搜集挖掘,因果学习可以发现变量之间的因果关系,进而构建有效的因果结构,因果结构是解决因果学习其他任务的基础前提。
二是因果量的识别。假设一个因果结构之间存在因果关系,那么因果学习可以帮助验证这个假设是否成立,同时把因果量转化为统计量。
三是因果效应评估。基于前两个任务的结果,因果学习可以实现评估一个或多个干预变量和结果变量之间的量化影响,包括从整体上、不同的群体上,甚至于个体上。
四是反事实推断,这是刚刚提到的因果学习的最高层级。当前世界没有办法观测到反事实结果,目前是通过反事实推断算法,尽可能准确地度量反事实状况下有可能产生的结果,这也是决策优化的一个重要工具。
五是策略学习,通常这是一个优化问题。基于前面建模的结果,策略学习能够进一步为特定目标提供决策选项以及定量分析的数据依据,最后帮助我们全局选择出最优的策略。
其中,因果发现旨在从一堆纷繁复杂的数据中,挖掘出不同变量之间因果影响的网络结构。为了进行因果发现,我们需要认识两个描述系统因果机制的工具:因果图和结构因果模型。
3.4. 因果效应评估
因果效应估计的传统方法是通过随机控制实验RCT(random controlled trials) ,因为随机实验的随机分配策略可以保证实验过程中没有混杂因素的存在,使得结果的不同只能由处理引起。然而随机实验的应用领域有限。
随着大数据的发展,如何仅从观察数据(observational data)中估计因果效应成为一项重要的课题。但该课题的实施存在两个难点:一是数据缺失的问题,从观察数据中我们只能得到实际结果,无法得知反事实结果;二是偏差的问题,收集观察数据的过程中,处理并不是随机分配的,即存在混杂因素,如果仅根据观察结果去估计因果效应,得到的结果是有偏的。
因果推断和机器学习其实是可以互相帮助的。在机器学习帮助因果推断方面,针对上述数据缺失的问题,引入机器学习模型可以大大提高反事实预测的准确率;而通过深度表征学习的方法,则可以对混杂因素变量进行调整,从而解决偏差的问题。在因果推断帮助机器学习方面,当前的机器学习方法追求的是预测的高精度(accuracy),引入因果推断则可以解决正确性(correctness)和可解释性(interpretability)的问题。
- 平均干预效果,详见3.2.1章节概述。
- DID双重差分(Differences-in-Differences)
DID 双重差分是对"平均因果效应评估"的改进,目的是进一步控制无关变量。采用双重差分法,必须分别获取实验组与对照组在实验前后两个时段的数据。
3.5. 因果推断Python开源工具
目前国际上关于因果推断的产品和工具也有很多,例如 CausaLML、EconML、CausaLearn、DoWhy 等等。不同产品和工具的侧重点都有所不同,例如 CausaLML 由 UBER 开源,定位是一个 uplift 建模专用的工具,主要解决因果效应评估类问题。EconML 由微软研究院开源,重点也是围绕因果效应评估类问题。还有 Causal-learn,专注于解决因果发现类问题。

3.5.1. DoWhy
「因果推断」(causal inference)是基于观察数据进行反事实估计,分析干预与结果之间的因果关系的一门科学。虽然在因果推断领域已经有许多的框架与方法,但大部分方法缺乏稳定的实现。DoWhy 是微软发布的一个用于进行端到端因果推断的 Python 库,其特点在于:
- 提供了一种原则性的方法将给定的问题转化为一张因果图,保证所有假设的明确性
- 提供了一种面向多种常用因果推断方法的统一接口,并结合了两种主要的因果推断框架
- 自动化测试假设的正确性及估计的鲁棒性
DoWhy通过四个基本步骤对工作流中的任何因果推断问题进行建模:模型,识别,估计和反驳。
- 模型: DoWhy使用因果关系图来模拟每个问题。当前版本的DoWhy支持两种图形输入格式:gml(首选)和点。该图可能包括变量中因果关系的先验知识,但DoWhy没有做出任何直接的假设。
- 识别:使用输入图,DoWhy根据图形模型找到识别所需因果效果的所有可能方法。它使用基于图形的标准和do-calculus来找到可以找到可以识别因果效应的表达式的潜在方法。
- 估计: DoWhy使用统计方法(如匹配或工具变量)估算因果效应。当前版本的DoWhy支持基于倾向的分层或倾向得分匹配的估计方法,这些方法侧重于估计治疗分配以及侧重于估计响应面的回归技术。
- 验证:最后,DoWhy使用不同的稳健性方法来验证因果效应的有效性。
3.5.2. YLearn
YLearn是一个因果学习算法工具包,这个名字是“learn why”的谐音。它主要支持因果学习任务中的各类相关任务,从因果效应识别(causal effect idenfitication),到因果效应估计(causal effect estimation),到因果发现(causal discovery)等等,都可以通过YLearn实现,最大程度地降低了学习一个因果工具的成本。
在YLearn中,关于因果推断流程有5个主要组成部分。
- 因果发现. 在观测数据中发现因果关系。
- 因果模型. 以 CausalGraph 的形式表示因果关系并做其他的相关操作比如用 CausalModel 识别。
- 估计模型. 使用不同的技术对因果估计量进行估计。
- 策略模型. 对每一个个体选择最好的策略。
- 解释器. 解释因果效应和策略。
这些组成部分被连接在一起形成一个完整的因果推断流程,被封装在一个API Why 中。
4. 大数据下因果推理
维克托《大数据时代》给我们提出了三个转变:
- 第一个转变就是,在大数据时代,我们可以分析更多的数据,有时候甚至可以处理和第一个转变就是,在大数据时代,我们可以分析更多的数据,有时候甚至可以处理和 某个特别现象相关的所有数据,而不再依赖于随机采样。 某个特别现象相关的所有数据,而不再依赖于随机采样。“样本=总体”
- 第二个改变就是,研究数据如此之多,以至于我们不再热衷于追求精确度。 第二个改变就是,研究数据如此之多,以至于我们不再热衷于追求精确度。
- 第三个转变因前两个转变而促成,即我们不再热衷于寻找因果关系,而应该寻找事物之间的相关关系。
我也片面的重视相关关系,而忽视了因果推理。而实际工作中,预测固然很重要,但是,从闭环管理视角来看,只是提出问题,而没有给出解决问题的辅助决策,也就进行因果推理,加上干预,评估解决问题。
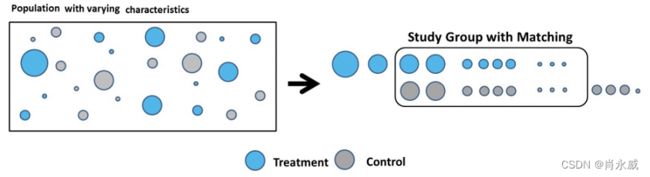
4.1. 如何使用更多维度的数据特征——倾向得分匹配(PSM)
这里倾向得分匹配(PSM,Propensity Score Matching)的思路是对策略命中的每一个用户,都在策略未命中用户中找到和他近似的一个用户。
4.1.1. 计算倾向性得分
关于PSM倾向性得分的计算方式,不能用简单的欧氏距离来计算是因为欧氏距离对每个协变量的权重是一样的,当协变量维度很高时会影响得分的计算效果。一般用LR来计算倾向性得分,因为LR能够赋予协变量不同的权重。还有很多方法比如用Propensity Tree来计算得分等等。
4.1.2. 匹配对照组样本
倾向性得分计算完成后,还需要为实验组的每个样本,从对照组中采集合适的样本去做匹配。PSM匹配环节有以下几个要点:
- 采样方式,有放回or无放回采样:从对照组抽取样本去匹配实验组样本时,被抽到的对照组样本是否允许放回。
- 匹配方式,局部最优or全局最优:应当追求为实验组每个样本找到的替身都是最匹配的(局部最优),还是整体来看实验组找到的替身是最匹配的(全局最优)。
- 匹配数量,一对一or一对多:一个实验组样本匹配一个对照组样本(一对一,偏差小,方差大),还是一个实验组用户匹配多个对照组用户(一对多,偏差大,方差小)。
- 匹配质量,有卡尺or无卡尺:实验组和对照组做匹配时,他们之间相似度是否需要限制在一定范围内(有卡尺),还是只要当前对照组样本是最匹配的即可(无卡尺)。
4.1.3. 平衡性检查
如何衡量PSM的匹配效果?或者说怎么判断PSM后实验组和对照组是否是同质的呢?下面介绍3种评估平衡性的方法:
- 观察法:直接做协变量分布的直方图或QQ-Plot,观察实验组和对照组的协变量是否符合同一分布。
- 量化法:计算每个混淆变量的标准化差值(stddiff),stddiff越小说明混淆变量在实验组和对照组间越均衡,因果效应的估计值也就越可靠。
- 卡方检验:每个协变量和treatment做卡方检验,若检验通过(p>0.05)则说明协变量和treatment是相互独立的,检验未通过(p<0.05)说明协变量对treatment是有影响的,因果效应中来自协变量的影响没有剔除干净。
目前为止,我们已经有一对接近同质的实验组和对照组了,接下来就可以估算实验的ATT了,最简单的做法是计算实验组和对照组均值的差值。
如果平衡性检查都通过了,说明已经得到了同质的实验组和对照组,下面就可以放心估计因果效应了。最简单的方法,是将两组样本均值直接做差,将差值作为因果效应的估计值。
4.1.4. 敏感度分析
如何衡量我们估计的因果效应是不是可靠的呢?具体地说,混淆变量的主观选择会得到不一样的结论吗?当干预变量T不存在时,因果效应还会存在吗?下面介绍常用的评估方法,即反驳测试:
- 安慰剂数据法:随机生成一列数据替代真实的treatment列,每个个体接收处理的事实已经不存在了,因此如果反驳测试中的因果效果大幅下降且接近0,说明了treatment对target具有一定的因果效应。
- 添加随机混淆变量法:添加一列随机生成的混淆变量,若反驳测试的因果效应较真实因果效应估计值变化不大,则说明其因果效应的估计值是可靠的。
4.2. 广义精确匹配(CEM)
广义精确匹配(CEM,Coarsened Exact Matching):主要是使用核心混杂因子(对“果”/“因变量” 影响较大的用户特征)进行匹配,每个实验用户匹配到的N个同特征用户作为对照组,取N个同特征用户的核心指标均值作为实验用户的对照。CEM主要用于用户量特别大的场景,在这种情况下预测倾向得分依赖于大量的计算资源和较优的模型效果,导致PSM会受到一定的影响。
4.3. 逆策略概率加权(IPTW)
逆策略概率加权(IPTW,Inverse Probability of Treatment Weighting):基于PSM,对策略效果进行加权计算,通俗来讲,就是样本越倾向选择这个策略,那么说明这个策略对该样本可能获得更好的策略效果,所以取逆得到的权重来平衡这个策略效果[3,4]。
4.4. 双重差分模型(DID)
双重差分模型(DID,Difference in Differences):本质是寻找自然对照组,是政策效果评估中常用的一种计量识别策略,原理是基于反事实框架来评估政策发生(e.g. A市开通高铁,实验组)和不发生(e.g. 与A市近似同质、且未开通高铁的B市,对照组)这两种情景下因变量(e.g. GDP增长)的变化。
4.5. 合成控制法(SCM)
合成控制法(SCM,Synthetic Control Methods):基于DID,基本思想是,我们通常很难找到与A市完全相似的B市,但通常可对若干大城市进行适当的线性组合,以构造一个更为优秀的“合成控制地区” (synthetic control region),并将“真实A市”与“合成A市”进行对比,故名“合成控制法”。合成控制法能够克服在选取对照对象时出现的样本选择偏误以及政策内生性问题。使用这个方法的一个关键点在于选择好最优权重矩阵,使得合成的对照组与实验组在treatment前的情况高度类似[5]。
4.6. 增益模型
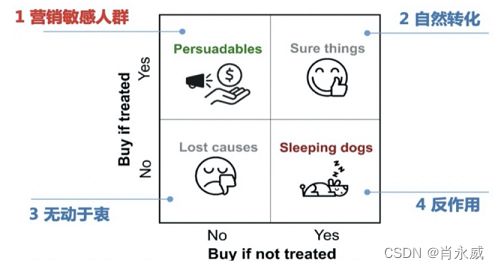
Uplift model:Uplift即为增益,Uplift models 主要用于预测一个treatment(e.g. 发优惠券)对个体(e.g. 给某个消费者)的增量价值(e.g. 这个消费者购买概率的提升值),实质上是因果推断中对ITE(Individual treatment effect )个体的因果效应的估计,常用于精准营销推荐算法的机器学习领域。
4.7. 断点回归
断点回归(RDD,Regression Discontinuity Design):基本思想是存在一个连续变量, 该变量能决定个体在某一临界点两侧接受政策干预的概率,由于X在该临界点两侧是连续的,因此个体针对X的取值落入该临界点任意一侧是随机发生的,即不存在人为操控使得个体落入某一侧的概率更大,则在临界值附近构成了一个准自然实验。学术界普遍认为断点回归的设计更接近准自然实验, 估计的结果更加准确。
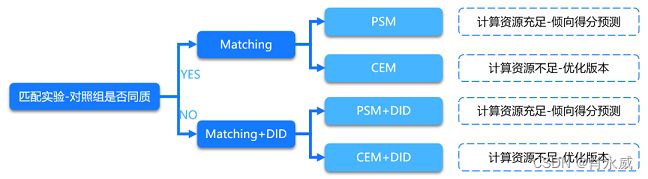
在大数据因果推理实际应用过程,例如应用在实际的业务效果/增量衡量中时,对于匹配类方法,在匹配得到同质的实验 vs 对照组的情况下,活动带来的业务效果即为活动开始后实验组和对照组的核心指标差值(Matching)。而当在通过以上匹配类方法没能找到完全同质的实验 vs 对照组的情况下,可依据匹配到的实验组和对照组用户,再结合DID的方法来去除干预前两组之间的GAP,通过匹配+DID类方法来计算因果效应(Matching+DID)。
5. 从预测到决策
5.1. 机器学习在现实中的困境
当前,人工智能正高速发展,其中最核心的贡献是机器学习,然而机器学习在大量应用过程中出现了瓶颈,主要有以下几方面:
一是泛化能力差。根据福布斯的数据,全球能够投入生产的机器学习项目只有 10% 左右,其中绝大部分项目没有投产的最重要原因就是泛化能力不足,导致模型在线上表现不稳定,达不到业务上的要求。这其中也存在多方面的原因,包括训练层面过拟合、欠拟合问题以及数据层面数据质量、数据漂移的问题,但最核心的问题还是来自于机器学习本身的基本原理:观测数据中相关关系的拟合。
基于统计上的相关关系其实并不可靠。以下的图表中有两条线,分别是十年期间每年尼古拉斯凯奇拍摄的电影数量和同年在泳池里溺水的人数的数量,从曲线中可以看到非常强的伪相关关系。我们可以训练一个非常准确的模型,但也明显的知道这是伪相关。伪相关是指不具备因果性影响的相关关系,如果机器学习模型里有一些重要的特征存在伪相关,那泛化能力的缺失就一定会成为一个问题。目前,泛化能力不足已经成为人工智能发展的巨大障碍。
二是缺乏解释性。当前,机器学习、深度学习在可解释性上面临着巨大的挑战,大部分研究成果还是围绕输入输出的相关关系做解释,没有完全说清楚因果关系的影响,所以可解释性也成为可信 AI 巨大的障碍。
三是对决策任务的支持能力不足。仅依靠对未来结果的预测很难提供有效的决策选项,也无法提供不同决策选项对未来结果可能产生的影响。实际上,从预测到决策还存在着巨大的差距。随着数字化转型的不断深入,企业并不满足于解决预测性任务,目前他们面临的是智能决策等更复杂的认知层面问题。
5.2. 什么是预测任务?什么是决策任务?
典型的预测任务包括预测某个产品未来的销量、未来有哪些用户有流失风险,有哪些客户可能会购买我的理财产品等,目前的机器学习算法已经能很好地完成这类任务。
决策问题则有一个明显的特点,就是更强调如何干预能够实现预期结果。比如,如何设定产品价格能够获得最高的销量、如何干预可以有效挽留有流失风险的用户、如何针对不同用户应该选择促销策略以提高购买转化率,这些都是典型的决策性任务。
商业智能分为几个阶段:从最基础的描述性分析、诊断性分析,告诉我们过去曾发生了什么;再上一个台阶到预测性分析,告诉我们未来有可能会发生什么,现在的机器学习算法主要还是停留在这个阶段的任务;再上一个台阶是指导性分析,告诉企业如果想实现一个目标应该怎么去做。
商业市场上同样呼吁应当加快因果学习技术的产业化应用。在Gartner最新发布的因果学习创新洞察报告《Innovation Insight:Causal AI》中指出, “人工智能必须超越基于相关性的预测,朝向基于因果关系的解决方案,以实现更好的决策和更大的自动化。……因果人工智能对未来至关重要。”
因果学习技术将大力提升人工智能技术的自主性、可解释性、适应性和鲁棒性。这些特性对于基于AI技术实现数智化升级的政府和企业来说,将进一步降本增效,并收获超预期的数据价值。
本人刚刚入门,欢迎讨论研究。
参考:
[1]. 中室牧子、津川友介. 原因与结果的经济学. 民主与建设出版社. 2019.08
[2]. 陈歪歪. 因果推断综述及基础方法介绍(一). 知乎. 2021.07
[3]. 打瞌睡的布偶猫. 因果推理综述——《A Survey on Causal Inference》一文的总结和梳理. 博客园. 2020.08
[4]. JeffffWang. 因果推断-PSM的原理及python实现. CSDN博客. 2022.08
[5]. CSDN 程序人生. 图灵奖得主 Judea Pearl:一场改变数据科学的“因果革命”,正席卷而来…. CSDN博客. 2020.06
[6]. 悟乙己. 活动、节假日、促销等营销方式的因果效应评估——方法模型篇(二). CSDN博客. 2022.05
[7]. 诡秘愚者. 因果推断学习笔记二.CSDN博客. 2021.07
[8]. 小葵向前冲. 机器学习------结构因果机制(SCM)、因果关系、因果推断. CSDN博客. 2021.09
[9]. 「已注销」. 因果推断-解决推荐系统公平性的新思路. CSDN博客. 2021.10
[10]. 赵小洛. 用因果推断解决的四类业务分析难题. 人人都是产品经理. 2022.06
[11]. 三更寒天. python对行为进行推理_微软开源了专注于因果推理的框架DoWhy. CSDN博客. 2021.01
[12]. 统计分析分析. PSM 倾向性匹配(一)基础知识 . CSDN博客. 2020.10
[13]. Anticoder. 因果推断—原理与方法(深度好文). 知乎. 2021.11
[14]. DataFun. [笔记] 因果推断常用评估指标. 简书. 2020.10
[15]. 木叶生. 概述:马尔可夫边界、因果发现和因果推理. 知乎. 2022.10
[16]. china1000. 因果推断总结. CSDN博客. 2022.08
[17]. 人工智能学家. 万字因果推断入门:为什么要做因果推断?. CSDN博客. 2022.09
[18]. DataFunTalk. 董彦燊:因果推断在哈啰出行的实践探索. 新浪网. 2022.02
[19]. CSDN资讯. 从预测到决策,九章云极DataCanvas 推出 YLearn 因果学习开源项目. CSDN博客. 2022.07
[20]. 机器之心Pro. 九章云极杨健:从预测到决策,YLearn全流程解决因果学习难题. 百度. 2022.09
[21]. 集智俱乐部. 什么是鲁宾因果框架|集智百科. 2021.10
[22]. 威化饼的一隅. 因果推理简介(causal inference). CSDN博客. 2021.12
[23]. Young Zicon. 基于潜在结果框架的因果效应估计(个人知识整理篇). 知乎. 2021.08
[24]. 口仆. 因果推断框架 DoWhy 入门. 知乎. 2020.12
[25]. YLearn与因果推断概述. 2022
[26]. 肖永威. 《大数据时代》读书笔记. CSDN博客. 2016.06
[27]. 阿里巴巴淘系技术团队官网博客. 因果推断:效应估计的常用方法及工具变量讨论. CSDN博客. 2022.03
[28]. 李小和 译. Jonas Peters. 因果推理基础与学习算法. 机械工业出版社. 2022.09