这次一定要弄懂-SVM-5-推广到soft margin svm和非线性的svm

有了前面推hard margin svm的经历，这次推soft margin svm应该会迅速很多。
开启～
昨晚还在B站上录制了一小段梳理整个SVM问题的视频：
https://www.bilibili.com/video/av62223878

5-1 Soft Margin SVM

5-1-1 Soft Margin SVM的原问题

hard margin svm是针对一个线性可分的数据集，用超平面对数据集进行划分。可是现实中线性可分的数据集是少数，所以我们需要改进hard margin svm，使其能够在非线性可分的数据集上也能使用

如何推广呢？
$$\underset{\omega }{\min }\frac{||\omega |{|}^2}{2}$$$$s.t.y^{(i)}({\omega }^T{\mathbf{x}}^{(\mathbf{i})}+b)⩾1\text{i=1,2,...m}$$

对于非线性可分的数据集，SVM在划分时，一定会存在错误，所以需要SVM算法有一定的容错能力。在一些情况下，可以把一些点错误的分类，同时希望最终的结果泛化能力还是很强的。

在Hard Margin SVM中，约束条件$$s.t.y^{(i)}({\omega }^T{\mathbf{x}}^{(\mathbf{i})}+b)⩾1\text{i=1,2,...m}$$就是要求所有的数据点都在Margin范围外，也就是所有的数据点都要在$w^T+b=1$与$w^T+b=-1$这两根直线外

现在为了让这些数据可以在margin区域内，所以要给他一个宽松量，宽松量为$\zeta$

所以现在我们要求
$$s.t.y^{(i)}({\omega }^T{\mathbf{x}}^{(\mathbf{i})}+b)⩾1-{\zeta }_i$$$${\zeta }_i⩾0\text{i=1,2,...m}$$

但是也不能让$\zeta$无限大，毫无约束，所以对目标函数也进行了修改为
$$\min \frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\zeta }_i$$

用C这个惩罚因子来平衡Soft Margin SVM中这两个部分的重要程度

也可以理解在Soft Margin SVM中添加了L1正则项

我们加入正则化项，让我们的模型相对于训练数据集有更高的容错能力，拥有了这种容错能力后，使得模型本身对训练数据集中的极端数据点不那么敏感，使得模型的泛化能力得到提升。

C越大，越在意松弛因子的大小，容错空间越小；C越小，越不在意松弛因子，容错空间越大

如果C取正无穷，则逼迫$\zeta$都为0，等价为Hard Margin SVM

对于Soft Margin SVM的原问题为
$$\min \frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\zeta }_i$$$$s.t.y^{(i)}({\omega }^T{\mathbf{x}}^{(\mathbf{i})}+b)⩾1-{\zeta }_i$$$${\zeta }_i⩾0\text{i=1,2,...m}$$

5-1-2 Soft Margin SVM的对偶问题

5-1-2-1 证明Soft Margin SVM满足Slater条件

证明Soft Margin SVM满足Slater条件，这样强对偶关系就成立了

目标函数为$$\min \frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\zeta }_i$$
是关于$w,\zeta$的凸优化问题

在寻找一组严格满足不等式约束的$w,b,\zeta$

令$w=0,b=0,\zeta =2$
则$y_i(w^T{x}_i+b)=0>1-\zeta =-1$
所以存在一组变量，使得不等式约束严格成立，故Slater条件满足，强对偶关系成立

5-1-2-2 对偶问题的推导

1.将不等式约束转换为标准形式$g(x)⩽0$
$y^{(i)}({\omega }^T{\mathbf{x}}^{(\mathbf{i})}+b)⩾1-{\zeta }_i$ ==== > $1-{\zeta }_i-y_i(w{x}_i+b)⩾0$
${\zeta }_i⩾0$ === > $-\zeta ⩽0$

2.构造拉格朗日乘子函数
$$L(w,b,\zeta ,\alpha ,\beta )=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\zeta }_i+\sum _{i=1}^m{\alpha }_i(1-{\zeta }_i-y_i(w{x}_i+b))-\sum _{i=1}^m{\beta }_i{\zeta }_i$$

3.对偶问题
即$\underset{\alpha ,\beta }{\max }\underset{w,b,\zeta }{\min }L(w,b,\zeta ,\alpha ,\beta )$
所以我们先求得令$L(w,b,\zeta ,\alpha ,\beta )$取最小的$w,b,\zeta$值
分别对$w,b,\zeta$求导得

$${\nabla }_{w}L(w,b,\zeta ,\alpha ,\beta )=w-\sum _{i=1}^m{\alpha }_i{y}_i{x}_i=0$$
$$\frac{\partial L(w,b,\zeta ,\alpha ,\beta )}{\partial b}=-\sum _{i=1}^m{\alpha }_i{y}_i=0$$
$${\nabla }_{\zeta }L(w,b,\zeta ,\alpha ,\beta )=C-{\alpha }_i-{\beta }_i=0$$
整理可得：
$$w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i$$$$\sum _{i=1}^m{\alpha }_i{y}_i=0$$$$C={\alpha }_i+{\beta }_i$$

4.将上面的解带入，得到$\underset{w,b,\zeta }{\min }L(w,b,\zeta ,\alpha ,\beta )$
$$\begin{gathered} \underset{w,b,\zeta }{\min }L(w,b,\zeta ,\alpha ,\beta )=\frac{1}{2}||w|{|}^2-\sum _{i=1}^m{\alpha }_i{y}_{i}b-\sum _{i=1}^m{\alpha }_i{y}_i{x}_{i}w+C\sum _{i=1}^m{\zeta }_i-\sum _{i=1}^m{\alpha }_i{\zeta }_i-\sum _{i=1}^m{\beta }_i{\zeta }_i+\sum _{i=1}^m{\alpha }_i \\ =-\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\alpha }_i \\ =-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j+\sum _{i=1}^m{\alpha }_i \end{gathered}$$
接下来就是调整乘子变量$\alpha ,\beta$求得最偶问题的最优解
$\underset{\alpha ,\beta }{\max }-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j+\sum _{i=1}^m{\alpha }_i$
等价于求
$\underset{\alpha ,\beta }{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j-\sum _{i=1}^m{\alpha }_i$

最后得到的对偶问题
$$\underset{\alpha ,\beta }{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j-\sum _{i=1}^m{\alpha }_i$$
$s.t.$
$${\alpha }_i⩾0,i=1,2,...m$$$${\beta }_i⩾0,i=1,2,...m$$$${\alpha }_i+{\beta }_i=C,i=1,2,...m$$$$\sum _{i=1}^m{\alpha }_i{y}_i=0$$

我们可以稍微整理下前3个不等式，将其合并为
$$0⩽{\alpha }_i⩽C$$

最终对偶问题为：
$$\underset{\alpha ,\beta }{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j-\sum _{i=1}^m{\alpha }_i$$
$s.t.$
$$0⩽{\alpha }_i⩽C$$$$\sum _{i=1}^m{\alpha }_i{y}_i=0$$
且

$$w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i$$
所以预测函数为
$$sgn(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i\cdot x_{预测样本}+b)$$

此时这还是一个线性模型，和线性可分的对偶问题相比，唯一的区别在于多了不等式约束。

相对于原问题，对偶问题的目标函数还是一个二次函数，但不等式和等式约束都更简单了，等式约束就是一条直线，不等式约束就是一个区间。

5-1-2-3 对偶问题是凸优化问题的证明

证明是凸优化问题，只需要证明可行域是凸集并且目标函数是凸函数即可。

由于对偶问题的等式约束和不等式约束都是线性约束，因此构成的集合是凸集。

同时我们将对偶问题写成向量形式
$$\begin{gathered} \underset{\alpha ,\beta }{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j-\sum _{i=1}^m{\alpha }_i \\ =\frac{1}{2}{\alpha }^T{Q}_{ij}\alpha -e^T\alpha \end{gathered}$$
其中$Q_{ij}=y_i{y}_j{X}_i^T{X}_j$,$e^T=[1,1,...,1]$
目标函数的Hessian矩阵为
$$Q=X^{T}X$$
令$X=[y_1{x}_1,y_2{x}_2,...y_m{x}_m]$

所以对于任意非0的向量x，有
$$x^{T}Qx=x^T{X}^{T}Xx=(Xx{)}^T(Xx)⩾0$$
因此矩阵Q半正定

5-2 加入核函数

在讲解线性分类器的时候，说到如何将线性分类器拓展到非线性的情形。

我们要做的就是先对已有的特征升维，在一个更高的维度进行线性分类。

比如我们原本只有x1这一维特征，对应的数据是线性不可分的，但如果我们添加一个维度$x_1^2$，则此时数据集就线性可分了。

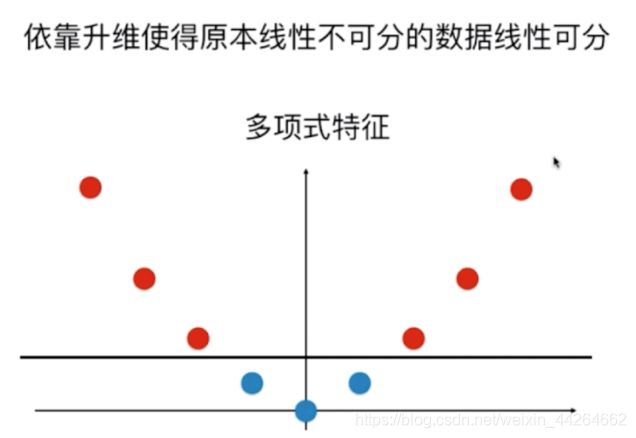
而核函数也是做的这样的事情，将原本的样本对应到高维的空间中，再进行线性分类。

5-2-1 以多项式核函数为例，理解核函数是如何运作的

在不使用核函数的时候，我们如果想将SVM拓展到非线性的情况，要做的是先把X->X’

假如我们的特征只有2个$X=[X_1,X_2]$
将其添加二次多项式$X^{\prime }=[X_1,X_2,X_1^2,X_2^2,X_1{X}_2]$

带入SVM对应的对偶问题中，则对有问题由原先的
$$\underset{\alpha ,\beta }{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{X}_i\cdot X_j-\sum _{i=1}^m{\alpha }_i$$
转化为
$$\underset{\alpha ,\beta }{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{X}_i^{\prime }\cdot X_j^{\prime }-\sum _{i=1}^m{\alpha }_i$$

同时预测函数由原来的
$$sgn(\sum _{i=1}^m{\alpha }_i{y}_i{X}_i\cdot X_{预测样本}+b)$$

转化为
$$sgn(\sum _{i=1}^m{\alpha }_i{y}_i{X}_i^{\prime }\cdot X_{预测样本}^{\prime }+b)$$

原本的操作是先将$X_i,X_j$转化为$X_i^{\prime },X_j^{\prime }$，再做点乘
有没有可能设置一个函数K，这个函数传入两个参数，参数为$X_i,X_j$，直接对原来的样本进行数学计算，直接算出$X_i^{\prime }\cdot X_j^{\prime }$
即$$K(X_i,X_j)=X_i^{\prime }\cdot X_j^{\prime }$$
相当于重新定义了点乘计算，同时使用K函数后，我们就不再需要先对数据升维再带入对偶问题中了，因为把原来的样本带入K函数中，求得的就是升维后点乘的结果。

这个K函数就叫做核函数

他是针对目标函数中存在$X_i\cdot X_j$点乘的式子或者类似这样的式子，都可以使用的一种数学技巧。对于一些复杂的变形，通常使用核函数可以减少计算量，同时节省存储空间。
因为用核函数，不需要存储变化后的高维数据，使用核函数就可以直接计算出点乘结果。

所以核函数不是SVM专用的一种思想。

我们用多项式核函数来验证下上面的思考
多项式核函数$$K(x,y)=(x\cdot y+c{)}^d$$

以d=2,c=1为例
$x=[x_1,x_2,...x_n]$
$y=[y_1,y_2,...y_n]$
$$\begin{gathered} K(x,y)=(x\cdot y+1{)}^2=(\sum _{i=1}^n{x}_i{y}_i+1{)}^2 \\ =(x_1{y}_1+x_2{y}_2+x_3{y}_3+...+x_n{y}_n+1)(x_1{y}_1+x_2{y}_2+x_3{y}_3+...+x_n{y}_n+1) \\ =\sum _{i=1}^n(x_i{)}^2(y_i{)}^2+\sum _{i=1}^{n-1}\sum _{j=i+1}^n(\sqrt{2}{x}_i{x}_j)(\sqrt{2}{y}_i{y}_j)+\sum _{i=1}^n(\sqrt{2}{x}_i)(\sqrt{2}{y}_i)+1 \end{gathered}$$

而
$x^{\prime }=[x_1^2,x_2^2,...,x_n^2,x_1{x}_2,x_1{x}_3,...x_{n-1}{x}_n,x_1,x_2,...x_3,1]$
$y^{\prime }=[y_1^2,y_2^2,...,y_n^2,y_1{y}_2,y_1{y}_3,...y_{n-1}{y}_n,y_1,y_2,...y_3,1]$
$x^{\prime }\cdot y^{\prime }=\sum _{i=1}^n(x_i{)}^2(y_i{)}^2+\sum _{i=1}^{n-1}\sum _{j=i+1}^n(x_i{x}_j)(y_i{y}_j)+\sum _{i=1}^n{x}_i{y}_i+1$

除了系数的微小差别外，$K(x,y)=x^{\prime }\cdot y^{\prime }$

所以我们可以直接用原来的样本数据，计算出$K(x,y)$,这个结果和我们先变换成x’y’，再进行点乘的结果是一致的，这样我们就完成了对样本添加二次项这样的特征。这就是核函数的优势，降低计算复杂度。

5-2-2 常见的核函数

不同的核函数，对应对原始数据样本进行不同的转换。

在sklearn中,主要提供4种核"linear",“poly”,“RBF”,“sigmoid”

其中

linear线性核函数	$K(x,y)=x\cdot y$
poly多项式核函数	$K(x,y)=(\gamma x\cdot y+c{)}^d$
rfb高斯核函数	$K(x,y)=e^{-r\Vert x-y{\Vert }^2}$
sigmoid	$tanh(\gamma x_i^T\cdot x_j+b)$

5-2-3 rbf高斯核函数

高斯核函数是SVM算法使用最多的一种核函数，核函数通常表示为$K(x,y)=e^{-r\Vert x-y{\Vert }^2}$，重新定义向量x,y的点乘。

其中只有一个超参数$\gamma$

高斯核函数和高斯分布（高斯函数）有什么联系呢？
仔细分析会发现，高斯核函数和高斯函数在表达式上有相似的形态。
高斯核函数$$K(x,y)=e^{-r\Vert x-y{\Vert }^2}$$
高斯函数$$g(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{1}{2}(\frac{x-\mu }{\sigma }{)}^2}$$

我们会发现高斯核函数中的$\gamma$和高斯分布中的$\frac{1}{2{\sigma }^2}$有共同的作用

所以可以猜测，小的$\gamma$对应大的$\sigma$，模型的复杂度越低。而大的$\gamma$对应小的$\sigma$，模型对训练数据太敏感，泛化能力低，容易过拟合。

对于多项式核函数的本质，其实是将我们所有的数据点首先添加多项式项，再将这些有了多项式项的新的数据特征进行点乘，形成了我们的多项式核

相应的，高斯核函数的本质，也是将我们原本的数据点先映射成一种新的特征向量，然后是这种新的特征向量点乘的结果。

高斯核函数背后对每一个样本点相应的变形是非常复杂的，但经过变形后进行点乘的结果的结果却非常简单。这样的一个式子，再次显示核函数的威力。它不需要我们具体计算出对于每一个样本点x和y到底先变成了一个怎样的样本点，我们只需要直接关注这样映射后的点乘结果。

用一个简单的例子来模拟高斯函数

为了方便可视化，对核函数进行一个改变，将y的值固定，也就是说，y不取样本点，而是取固定的点，取2个固定的点当y。

这2个固定的点分别叫l1,l2,英文为landmark，中文翻译为地标。

高斯核函数做的升维过程就是，对于原本的每一个x值，如果我们有两个地标的话，就把它升维成一个二维的样本点。

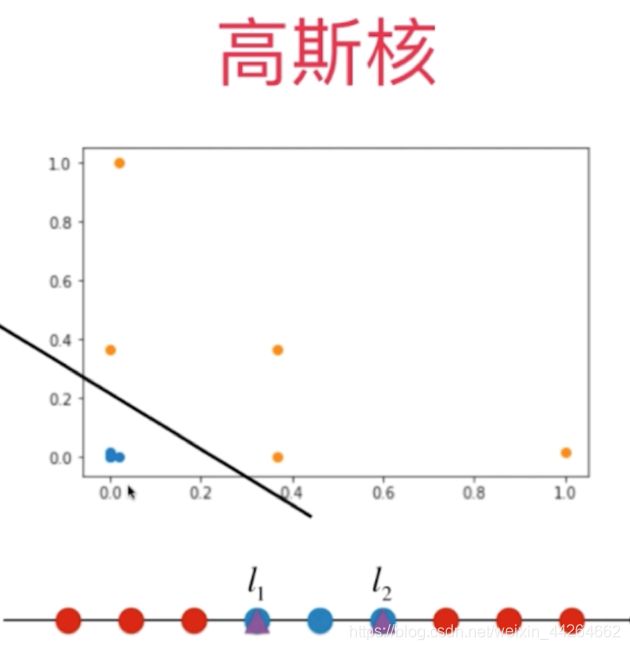
实际高斯核函数中，y的位置是每一个数据点。换句话说，高斯核函数干的事情和我们之前干的事情一样，只不过那个地标点比我们之前取得要多得到。

样本有多少个，就有多少个地标点。换句话说，对于每一个样本x，它都尝试对每一个样本y进行一个核函数的计算，称为新的高维空间中对应的某一个维度元素。

高斯核函数的本质就是将原本的数据映射进了一个无穷维的空间。所谓的无穷可以理解为由于样本数据点是有无穷多个，所以它映射进了一个无穷维的空间。

但具体拿到一组数据的时候，因为m是有限个，所以它映射成了m*m这样的数据。

我们在使用高斯核函数时，由于这个映射过程，所以计算开销非常大。因此，SVM使用高斯核函数的训练时间比较长。尽管如此，还是存在非常适合使用高斯核函数的样本集。

最典型的应用就是如果我们初始的样本数据维度非常高，但是样本数据的数量可能并不多。换句话说，也就是当m

5-3 SMO算法

5-3-1 KKT条件

KKT条件的中要求
${\mu }_k{g}_k(x^{\ast })=0$

我们的原问题中存在两个不等式约束:
$y_i(w^T{X}_i+b)⩾1-{\zeta }_i$
${\zeta }_i⩾0$

所以对应的KKT条件为
${\alpha }_i(y_i(w^T{X}_i+b)-1+{\zeta }_i)=0$
${\beta }_i{\zeta }_i=0$
$i=1,2,...m$

接下来分情况讨论${\alpha }_i$
在对偶问题中，我们知道${\alpha }_i$的不等式约束为
$0⩽{\alpha }_i⩽C$

故${\alpha }_i$的取值有三种情况:

1. ${\alpha }_i=0$
   则 $y_i(w^T{X}_i+b)-1+{\zeta }_i⩾0$
   由因为${\alpha }_i+{\beta }_i=C$，
   故${\beta }_i=C$
   因为${\beta }_i{\zeta }_i=0$
   故${\zeta }_i=0$
   最终$y_i(w^T{X}_i+b)⩾1$

2. ${\alpha }_i=C$
   则${\beta }_i=0$,${\zeta }_i⩾0$
   又因为$y_i(w^T{X}_i+b)-1+{\zeta }_i=0$
   故$y_i(w^T{X}_i+b)=1-\zeta ⩽1$

3. $0<{\alpha }_i<C$
   故$y_i(w^T{X}_i+b)-1+{\zeta }_i=0$
   又因为${\beta }_i>0$,所以${\zeta }_i=0$
   所以$y_i(w^T{X}_i+b)=1$

最终总结一下：
$$\{\begin{array}{llc}{\alpha }_i=0& y_i(w^T{X}_i+b)⩾1& 对应自由变量，对确定分类超平面不起作用\\ 0<{\alpha }_i<C& y_i(w^T{X}_i+b)=1& 支撑向量\\ {\alpha }_i=C& y_i(w^T{X}_i+b)⩽1& 违反了不等式约束，进行了惩罚\end{array}$$

KKT条件用于：

1. SMO算法选择优化变量
2. 2.迭代终止的判定规则

5-3-2 SMO算法

5-3-2-1求解子问题

假设我们已经选出了优化变量KaTeX parse error: Expected 'EOF', got '\alpah' at position 1: \̲a̲l̲p̲a̲h̲_1和${\alpha }_2$

因为将除${\alpha }_1$和${\alpha }_2$以外的变量看作是常数，所以对偶问题可以写成以下形式的二元二次函数的形式

其中$K_{ij}=K(X_i,X_j)$

$$\begin{gathered} \underset{\alpha ,\beta }{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{K}_{ij}-\sum _{i=1}^m{\alpha }_i \\ =\frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+y_1{y}_2{K}_{12}{\alpha }_1{\alpha }_2+y_1{\alpha }_1\sum _{j=3}^m{\alpha }_j{y}_j{K}_{1j}+y_2{\alpha }_2\sum _{j=3}^m{\alpha }_j{y}_j{K}_{2j}-{\alpha }_1-{\alpha }_2+c \end{gathered}$$

为了方便表示，定义
$s=y_1{y}_2$
$v_i=\sum _{k=3}^m{y}_k{\alpha }_k{K}_{ik}$

故上式为
$=\frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+s{K}_{12}{\alpha }_1{\alpha }_2+y_1{v}_1{\alpha }_1+y_2{v}_2{\alpha }_2-{\alpha }_1-{\alpha }_2+c$

根据约束条件$y_1{\alpha }_1+y_2{\alpha }_2=-\sum _{k=3}^m{y}_k{\alpha }_k=\xi$
故${\alpha }_1=y_1\xi -s{\alpha }_2$
令$w=y_1\xi$
则${\alpha }_1=w-s{\alpha }_2$

带入上式，求出关于${\alpha }_2$的函数，并求极值点
上式为
$=(\frac{1}{2}{K}_{11}+\frac{1}{2}{K}_{22}-K_{12}){\alpha }_2^2-(ws{K}_{11}-ws{K}_{12}+s{y}_1{v}_1-y_2{v}_2+1-s){\alpha }_2+c^{\prime }$

接下来我们要求对应的极值点，所以可以通过求一阶导数，并令其为0，得
$(K_{11}+K_{22}-2K_{12}){\alpha }_2=ws{K}_{11}-ws{K}_{12}+s{y}_1{v}_1-y_2{v}_2+1-s$
等号右边可以进一步化简为
${\alpha }_2^{old}(K_{11}+K_{22}-2K_{12})+y_2((u_1-y_1)-(u_2-y_2))$

为了让表达式看起来更整洁
令
$\eta =K_{11}+K_{22}-2K_{12}$
$E_i=u_i-y_i$即原来的预测值与真实值之间的差距
则${\alpha }_2^{unclipped}={\alpha }_2^{old}+\frac{y2(E_1-E_2)}{\eta }$

但由于${\alpha }_2$是有约束的，所以最终的${\alpha }_2$不一定就是${\alpha }_2^{unclipped}$
所以我们需要计算下${\alpha }_2$的取值范围

关于${\alpha }_2$和${\alpha }_1$的取值要求有
${\alpha }_1{y}_1+{\alpha }_2{y}_2=-\sum _{i=3}^m{\alpha }_i{y}_i=\xi$
$0⩽{\alpha }_1⩽C$
$0⩽{\alpha }_2⩽C$

通过分类讨论和画图，最终可以得到
$$\{\begin{array}{llc}L=\max \{{\alpha }_1+{\alpha }_2-C,0\}& H=\min \{{\alpha }_1+{\alpha }_2,C\}& y_1{y}_2=1\\ L=\max \{0,{\alpha }_2-{\alpha }_1\}& H=\min \{C+{\alpha }_2-{\alpha }_1,C\}& y_1{y}_2=-1\end{array}$$

所以消元后，最终${\alpha }_2^{new}$为
$${\alpha }_2^{new}=\{\begin{array}{ll}H& {\alpha }_j^{unclipped}>H\\ {\alpha }_j^{unclipped}& L⩽{\alpha }_j^{unclipped}⩽H\\ L& {\alpha }^{unclipped}<L\end{array}$$

因为要满足等式约束${\alpha }_1^{new}{y}_1+{\alpha }_2^{new}{y}_2={\alpha }_1^{old}{y}_1+{\alpha }_2^{old}{y}_2$
${\alpha }_1^{new}={\alpha }_1^{old}+s({\alpha }_2^{old}-{\alpha }_2^{new})$

5-3-2-2 优化变量的寻找

${\alpha }_1$的寻找：
SMO算法称第1个变量的寻找过程为外层循环。外层循环在训练样本中选取违反KKT条件最严重的样本点，将其对应的变量作为第1个变量。具体地，检查训练样本点$(x_i,y_i)$是否满足KKT条件，即
$$\{\begin{array}{llc}{\alpha }_i=0& y_{i}g(x_i)⩾1& 对应自由变量，对确定分类超平面不起作用\\ 0<{\alpha }_i<C& y_{i}g(x_i)=1& 支撑向量\\ {\alpha }_i=C& y_{i}g(x_i)⩽1& 违反了不等式约束，进行了惩罚\end{array}$$
其中，$g(x_i)=\sum _{j=1}^m{\alpha }_j{y}_{j}K(x_i,x_j)+b$

这个检验是在$ϵ$范围内进行的，检查过程中，外层循环首先遍历所有满足条件$0<{\alpha }_i<C$的样本点，即在间隔边界上的支持向量点，检验它们是否满足KKT条件。如果这些样本点都满足KKT条件，那么遍历整个训练集，检验它们是否满足KKT条件

第2个变量${\alpha }_2$的选择
SMO算法称选择第2个变量的过程为内层循环。假设在外层循环中已经找到第1个变量${\alpha }_1$，现在要在内层循环中找第2个变量${\alpha }_2$。第2个变量选择的标准是希望能够使${\alpha }_2$有足够大的变化

之前的推导中发现${\alpha }_2^{unclipped}$是依赖于$|E_1-E_2|$，为了加快计算速度，一种简单的做法是选择${\alpha }_2$，使其对应的$|E_1-E_2|$最大。为了节省计算时间，将所有的|E_i|值保存在一个列表中。

5-3-2-3 计算阈值b和差值$E_i$

每次计算阈值b
根据KKT条件
$b_1^{new}=b^{\ast }-E_1+y_1{K}_{11}({\alpha }_1^{\ast }-{\alpha }_1^{new})+y_2{K}_{21}({\alpha }_2^{\ast }-{\alpha }_2^{new})$
$b_2^{new}=b^{\ast }-E_2+y_1{K}_{12}({\alpha }_1^{\ast }-{\alpha }_1^{new})+y_2{K}_{22}({\alpha }_2^{\ast }-{\alpha }_2^{new})$

按照李航老师的说法

这一部分的理论推导通过看知乎上的一篇文章弄懂了
（1）当${\alpha }_1^{new}$和${\alpha }_2^{new}$都在0,C之间，根据${\alpha }_1$和${\alpha }_2$的关系曲线可以知道，此时${\alpha }_2$不再边界点上取得最小值，所以${\alpha }_2^{new}={\alpha }_2^{unclipped}$
故${\alpha }_2$为$(K_{11}+K_{22}-2K_{12}){\alpha }_2=ws{K}_{11}-ws{K}_{12}+s{y}_1{v}_1-y_2{v}_2+1-s=0$的点
根据这个式子，可以推导出$b_1^{new}$和$b_2^{new}$的等式
（2）当${\alpha }_1^{new}$和${\alpha }_2^{new}$同时不满足0,C之间，则根据${\alpha }_1$和${\alpha }_2$的关系曲线，当y1y2== 1时，只能一个为0，一个为C；当y1y2== -1时，只能同时为0或者同时为C，经过推导可以知道，$b^{new}$必须在$[b_1^{new},b_2^{new}]$之间

所以最终b的取值为
$$\{\begin{array}{ll}{b}_1^{new}& 0<{\alpha }_1^{new}<C\\ b_2^{new}& 0<{\alpha }_2^{new}<C\\ \frac{b_1^{new}+b_2^{new}}{2}& otherwise\end{array}$$

5-4 总结SVM

将原问题转化为对偶问题，通过SMO算法，求得对偶问题的最佳解。

5-5 python实现

建立数据集

import numpy as np
import matplotlib.pyplot as plt

X=np.array([
            [-1,6],
            [1,5],
            [1,7],
            [3,3],
            [5,4],
            [2,0]])
y=np.array([1,1,1,-1,-1,-1])

plt.scatter(X[y==1,0],X[y==1,1],label='+',color='r')
plt.scatter(X[y==-1,0],X[y==-1,1],label='-',color='b')
plt.legend()

涉及到的公式和流程
1.初始化alpha,E,C,b
2.根据kkt条件选取优化变量
$$\{\begin{array}{llc}{\alpha }_i=0& y_{i}g(x_i)⩾1& 对应自由变量，对确定分类超平面不起作用\\ 0<{\alpha }_i<C& y_{i}g(x_i)=1& 支撑向量\\ {\alpha }_i=C& y_{i}g(x_i)⩽1& 违反了不等式约束，进行了惩罚\end{array}$$

class SVM:
    def __init__(self,kernel='linear',max_iter=200):
        self.max_iter = max_iter
        self._kernel = kernel
    
    def _calE(self,i):
        return self._u(i)-self.y[i]
    
    def _u(self,i):
        return np.sum(self.X.dot(self.X[i])*self.alpha*self.y)+self.b
    
    def _KKT(self,i):
        yu = self._u(i)*self.y[i]
        if np.abs(self.alpha[i] - 0) <= self.epsilon:
            return yu >= 1+self.epsilon
        elif 0<self.alpha[i]<self.C:
            return np.abs(yu - 1) <= self.epsilon
        else:
            return yu <= 1-self.epsilon

    def kernel(self,i,j):
        if self._kernel == 'linear':
            return self.X[i].dot(self.X[j])
    
    def _new_alpha(self,i,j):
        if self.y[i]== self.y[j]:
            L = max(0,self.alpha[i]+self.alpha[j]-self.C)
            H = min(self.C,self.alpha[i]+self.alpha[j])
        else:
            L = max(0,self.alpha[j]-self.alpha[i])
            H = min(self.C,self.C+self.alpha[j]-self.alpha[i])
        
        eta = self.kernel(i,i)+self.kernel(j,j)-2*self.kernel(i,j)
        if eta==0:
            print("bug",i,j)
        alpha_2_un = self.alpha[j]+self.y[j]*(self.E[i]-self.E[j])/eta
        
        if alpha_2_un > H:
            alpha_2_new = H
        elif alpha_2_un < L:
            alpha_2_new = L
        else:
            alpha_2_new = alpha_2_un
        
        alpha_1_new=self.alpha[i]+self.y[i]*self.y[j]*(self.alpha[j]-alpha_2_new)
        
        return alpha_1_new,alpha_2_new
        
        
    
    def fit(self,features,labels,C=1,epsilon=1e-3):
        
        self.X = features
        self.y = labels
        self.b = 0
        self.C = C
        self.alpha = np.zeros(len(self.X))
        self.epsilon=epsilon
        self.E = np.array([self._calE(k) for k in range(len(self.X))])
        self.w = 0
        
        for internum in range(self.max_iter):
            
            index_list = np.array(np.where(self.alpha > self.epsilon)).flatten()
            non_list = np.array(np.where(abs(self.alpha) <= self.epsilon)).flatten().copy()
            all_list = np.hstack([index_list,non_list])
            
            for k in all_list:
                if self._KKT(k):
                    continue
                
                j_index = index_list[index_list!=k]
                j_non = non_list[non_list!=k]
                if(len(j_index))>1:
                    E_temp=np.abs(self.E[j_index]-self.E[k])
                    j=j_index[np.argmax(E_temp)]
                    i=k
                    break
                else:
                    E_temp=np.abs(self.E[j_non]-self.E[k])
                    j=j_non[np.argmax(E_temp)]
                    i=k
                    break
            
            
            alpha_1_new,alpha_2_new=self._new_alpha(i,j)
            
            b1_new = -self.E[i]-self.y[i]*self.kernel(i,i)*(alpha_1_new-self.alpha[i])-self.y[j]*self.kernel(j,i)*(alpha_2_new-self.alpha[j])+self.b
            b2_new = -self.E[j]-self.y[i]*self.kernel(i,j)*(alpha_1_new-self.alpha[i])-self.y[j]*self.kernel(j,j)*(alpha_2_new-self.alpha[j])+self.b
        
            if 0 < alpha_1_new <self.C:
                b_new = b1_new
            elif 0 < alpha_2_new <self.C:
                b_new = b2_new
            else:
                b_new = (b1_new+b2_new)/2
        
            self.alpha[i]=alpha_1_new
            self.alpha[j]=alpha_2_new
            self.b = b_new
            
            
            for k in range(len(self.X)):
                self.E[k]=self._calE(k)
 
        self.w = self._weight()
    def _weight(self):
        return np.sum(self.X*np.tile(self.y.reshape(-1,1),(1,self.X.shape[1]))*np.tile(self.alpha.reshape(-1,1),(1,self.X.shape[1])),axis=0)
       

clf = SVM()
clf.fit(X,y,C=1000)
clf.alpha
w3 = clf.w
b3 = clf.b
clf.alpha

array([0.   , 0.132, 0.   , 0.132, 0.   , 0.   ])

x_plot=np.linspace(-1,5,10000)
y_plot=(-b-w[0]*x_plot)/w[1]

plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==-1,0],X[y==-1,1])
plt.plot(x_plot,y_plot)

from sklearn.svm import LinearSVC
clf = LinearSVC()
clf.fit(X,y)
w0=clf.coef_
b0=clf.intercept_
x_plot=np.linspace(-1,5,1000)
y_plot=(-b-w[0]*x_plot)/w[1]
y_plot2=(-b0-w0[0,0]*x_plot)/w0[0,1]
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==-1,0],X[y==-1,1])
plt.plot(x_plot,y_plot)
plt.plot(x_plot,y_plot2)

from sklearn.datasets import load_iris
iris=load_iris()
X=iris.data[iris.target!=2]
X=X[:,0:2]
y=iris.target[iris.target!=2]
y[y==0]=-1

clf = SVM(max_iter=1000)
clf.fit(X,y,C=1000)
clf.alpha
w = clf.w
b = clf.b
clf.alpha

array([ 0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00, -2.22044605e-16,  0.00000000e+00,
        7.67179484e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  2.52991452e+01,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  3.29709400e+01,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
        0.00000000e+00,  0.00000000e+00,  0.00000000e+00,  0.00000000e+00])

x_plot=np.linspace(4,7,10000)
y_plot=(-b-w[0]*x_plot)/w[1]
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==-1,0],X[y==-1,1])
plt.plot(x_plot,y_plot)

from sklearn.svm import LinearSVC
clf = LinearSVC(C=1000)
clf.fit(X,y)
w0=clf.coef_
b0=clf.intercept_
x_plot=np.linspace(4,7,1000)
y_plot=(-b-w[0]*x_plot)/w[1]
y_plot2=(-b0-w0[0,0]*x_plot)/w0[0,1]
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==-1,0],X[y==-1,1])
plt.plot(x_plot,y_plot,label='myself')
plt.plot(x_plot,y_plot2,label='svm')
plt.legend()

/anaconda3/lib/python3.7/site-packages/sklearn/svm/base.py:931: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  "the number of iterations.", ConvergenceWarning)

代码写的还很幼稚，以后有机会会继续修改的。

参考资料：
https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/tr-98-14.pdf