第五届传智杯 | 初赛 | python 解法思路复盘
文章目录
- A-莲子的软件工程学
-
- 题目描述
- 输入格式
- 输出格式
- 样例
- 我的思路
-
- 源代码
- B-莲子的机械动力学
-
- 题目描述
- 输入格式
- 输出格式
- 样例
- 我的思路
-
- 源代码
- E-梅莉的市场经济学
-
- 题目描述
- 输入格式
- 输出格式
- 样例
- 我的思路
-
- 源代码
A-莲子的软件工程学
题目描述
具体而言,给定两个整数 a , b a,b a,b,保证 b ≠ 0 b\neq 0 b=0。莲子要实现这样一个函数 fun ( a , b ) \operatorname{fun}(a,b) fun(a,b) 来将 b b b 的符号转移到 a a a 上。
具体而言, fun ( a , b ) = sgn ( b ) × ∣ a ∣ \operatorname{fun}(a,b)=\operatorname{sgn}(b)\times |a| fun(a,b)=sgn(b)×∣a∣。其中, sgn ( b ) = { 1 b > 0 − 1 b < 0 \operatorname{sgn}(b)=\begin{cases}1&b>0\\-1&b<0\end{cases} sgn(b)={1−1b>0b<0
换而言之:
- 如果 b b b 是正数,那么 fun ( a , b ) = + ∣ a ∣ = ∣ a ∣ \operatorname{fun}(a,b)=+|a|=|a| fun(a,b)=+∣a∣=∣a∣;
- 如果 b b b 是负数,那么 fun ( a , b ) = − ∣ a ∣ \operatorname{fun}(a,b)=-|a| fun(a,b)=−∣a∣。
如果使用一个三维坐标系描述 fun ( a , b ) \operatorname{fun}(a,b) fun(a,b),则应当如下图所示:
你只需输出 fun ( a , b ) \operatorname{fun}(a,b) fun(a,b) 的值。
输入格式
- 共一行两个整数 a , b a,b a,b。
输出格式
- 共一行一个整数 fun ( a , b ) \operatorname{fun}(a,b) fun(a,b) 的值。
样例
样例输入
-1 2
样例输出
1
样例输入
0 -4
样例输出
0
样例输入
-12345 -54321
样例输出
-12345
提示
对于全部数据,保证 a , b a,b a,b 在 32 32 32 位有符号整型范围内,并且 b ≠ 0 b \neq 0 b=0。
我的思路
第一次打开传智杯的题目,又是给图又是描述的,看得出传智杯的题目风格很严谨,篇幅稍长。
A题打卡题,只要稍微熟悉一点语言就没问题,用abs()绝对值函数可以省事很多
源代码
a,b=map(int,input().split(' '))
def sub(b):
if b>0:
return 1
else:return -1
def fun(a,b):
return abs(a)*sub(b)
print(fun(a,b))
相比看来,python代码似乎的却很简洁
B-莲子的机械动力学
题目描述
题目背景的问题可以转化为如下描述:
给定两个长度分别为 n , m n,m n,m 的整数 a , b a,b a,b,计算它们的和。
但是要注意的是,这里的 a , b a,b a,b 采用了某种特殊的进制表示法。最终的结果也会采用该种表示法。具体而言,从低位往高位数起,第 i i i 位采用的是 i + 1 i+1 i+1 进制。换言之,相较于十进制下每一位的「逢 10 10 10 进 1 1 1」,该种进制下第 i i i 位是「逢 i + 1 i+1 i+1 进 1 1 1」。
下图所示,左边是十进制的竖式加法;右边是这种特殊进制的竖式加法。图中的红色加号表示上一位发生了进位。
输入格式
- 第一行有两个整数 n , m n,m n,m,分别表示 a a a 和 b b b 的位数。
- 第二行有 n n n 个整数,中间用空格隔开,从高到低位描述 a a a 的每个数码。
- 第三行有 m m m 个整数,中间用空格隔开,从高到低位描述 b b b 的每个数码。
输出格式
- 输出有若干个整数,从高到低位输出 a + b a+b a+b 在这种特殊表示法下的结果。
样例
样例输入
5 4
3 3 2 1 1
3 2 2 1
样例输出
4 2 1 1 0
样例输入
10 1
10 9 8 7 6 5 4 3 2 1
0
样例输出
10 9 8 7 6 5 4 3 2 1
提示
对于全部数据,保证 1 ≤ n , m ≤ 2 × 1 0 5 1\le n,m\le 2\times 10^5 1≤n,m≤2×105,从低位往高位数起有 a i ∈ [ 0 , i ] a_i\in[0,i] ai∈[0,i], b i ∈ [ 0 , i ] b_i\in[0,i] bi∈[0,i]。请使用 Java 或 Python 语言作答的选手注意输入输出时的效率。
我的思路
-
读懂题目:
看着题目背景一开始被吓到了,那么长、又是进制题。但耐心读下来发现,其实就是解决一个随着位数增长、进制数也一起增长的特别的加法而已 -
输入数据预处理:
输入两个数组不等长,为方便加法,两个数组都在高位补零至等长,长度为两个数组中较长的数组长度+1,加一是因为在最高位做加法时也可能进位 -
核心加法部分:
抱着脑袋想一会儿,会发现进制数随数组位数改变,且这个改变是固定的,进制数=数组位数+2
再想一会儿,会发现每位做加法时,位的值=两个数的和%进制数(取模),而加法在进位时,设进位的值为temp,那么temp=两个数的和//进制数(整除) -
丢分反思:
(1)没想到最高位进位时候的情况,导致一些数据集错误
(2)进位的值的逻辑差了一小点,导致做加法时有瑕疵,就差了这句:
- 时间复杂度:遍历一遍数组长度,应该是O(n)
temp = 0 #每次加法后进位值要初始化成0
源代码
n,m=map(int,input().split(' '))
a=list(map(int,input().split(' ')))
b=list(map(int,input().split(' ')))
a=a[::-1] #倒转数组
b=b[::-1]
sum=[]
ma_le=max(len(a),len(b))
mi_le=min(len(a),len(b))
#2.输入数据预处理:
#输入两个数组不等长,为方便加法,两个数组都在高位补零至等长,
#长度为两个数组中较长的数组长度+1,加一是因为在最高位做加法时也可能进位
for i in range(ma_le-mi_le+1):
if len(a)<len(b):
a.append(0)
else:b.append(0)
if len(a)<len(b):
a.append(0)
else:b.append(0)
# 核心加法部分
temp=0 #设进位的值为temp
for i in range(ma_le+1): #遍历 较长数组长度加一 次
ad=a[i]+b[i]+temp #每位两个数字加进位值的总和
temp = 0 #每次加法后进位值要初始化成0
if ad>=i+2: #发生进位
sum.append(ad%(i+2)) #位的值=两个数的和%进制数
temp=ad//(i+2) #进位值=两个数的和//进制数
elif ad<i+2: #不发生进位
sum.append(ad)
#最高位可能有0冗余,格式化后输出
sum=sum[::-1]
if len(sum)>1:
if sum[0]==0:
sum.remove(0)
# 输出格式
for i in sum:
print(i,end=' ')
E-梅莉的市场经济学
题目描述
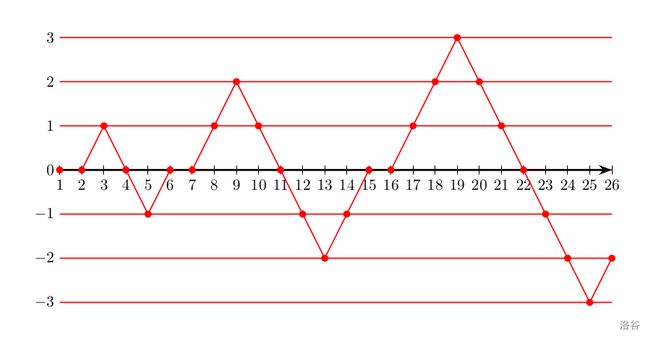
市场每一天的贸易差可以视为一个有周期性规律的数列 a a a: [ 0 ] , [ 0 , 1 , 0 , − 1 , 0 ] , [ 0 , 1 , 2 , 1 , 0 , − 1 , − 2 , − 1 , 0 ] , [ 0 , 1 , 2 , 3 , 2 , 1 , 0 , − 1 , − 2 , − 3 , − 2 , − 1 , 0 ] … \color{red}[0],\color{blue}[0,\allowbreak 1,\allowbreak 0,\allowbreak -1,\allowbreak 0],\color{red}[0,\allowbreak 1,\allowbreak 2,\allowbreak 1,\allowbreak 0,\allowbreak -1,\allowbreak -2,\allowbreak -1,\allowbreak 0],\allowbreak \color{blue}[0,\allowbreak 1,\allowbreak 2,\allowbreak 3,\allowbreak 2,\allowbreak 1,\allowbreak 0,\allowbreak -1,\allowbreak -2,\allowbreak -3,\allowbreak -2,\allowbreak -1,\allowbreak 0]\dots [0],[0,1,0,−1,0],[0,1,2,1,0,−1,−2,−1,0],[0,1,2,3,2,1,0,−1,−2,−3,−2,−1,0]… 具体而言, a a a 可以被分为无穷段,第 i i i 段的内容为 { 0 , 1 , ⋯ , i , i − 1 , ⋯ , 0 , − 1 , ⋯ , − i , − i + 1 , ⋯ 0 } \{0,\allowbreak 1,\allowbreak \cdots,\allowbreak i,\allowbreak i-1,\allowbreak \cdots,0,\allowbreak -1,\allowbreak \cdots,\allowbreak -i,\allowbreak -i+1,\allowbreak \cdots 0\} {0,1,⋯,i,i−1,⋯,0,−1,⋯,−i,−i+1,⋯0}。如下图所示,是将 a a a 数列内的前一些点绘制在坐标轴上的情况:
现在梅莉对市场发起了 q q q 次询问,每次她会给定一个 k k k,希望求出 a k a_k ak 是多少。
输入格式
- 第一行有一个正整数 q q q,表示询问次数。
- 接下来 q q q 行,每行一个正整数 k k k,描述每次询问。
输出格式
- 输出共 q q q 行。对于每次询问,输出对应的结果。
样例
样例输入
9
1
10
100
1000
10000
100000
1000000
10000000
100000000
样例输出
0
1
6
-9
-11
-128
406
1629
5154
提示
对于所有数据, 1 ≤ q ≤ 1 0 5 1 \leq q \leq 10^5 1≤q≤105, 1 ≤ k ≤ 4 × 1 0 18 1 \leq k \leq 4\times 10^{18} 1≤k≤4×1018。
我的思路
- 理解题目:
构造出上面那个分段波形图,输入一串X坐标的值,输出X在图中对应的Y值 - 求出X所在波形的顶点:
图形由有规律的波形衔接而成,每个波形的顶点top依次加一,每个波形的横坐标长度为top*4,找到这个规律就能推算出每个以top为编号的波形在x轴上的位置。 既然输入的是X值,那就找到此X所在的波形(找对应的top)
具体地,就是用高中的等差数列求和公式,可以构造出一个求位置方程0=2top^2+3*top+1-x,这个方程的对称轴为-3/4,开口向上,定义域为0到正无穷,所以,对这个方程使用求根公式并向上取整就能得出此时X所在波形的top:
top= ceil((-3 + sqrt(1 + 8 * x)) / 4) #每个波形的顶点值
- 找波形内相对位置:
找到此波形的top了,就能用求位置方程 得出上一个波形的结束位置last_dot = top + 2 * (top - 1) * ((top - 1) + 1),以此就能计算此时X在此波形中的相对位置rel_dot = x - last_dot - 1 - 分段函数的反思:
相对位置也找到了,接下来只需把每个波形的三段分别用top和相对位置表示出来即可,规律很好找,有能力还可以用pyplot 工具画一个图,对比题目里面图的一模一样就不会出现纰漏了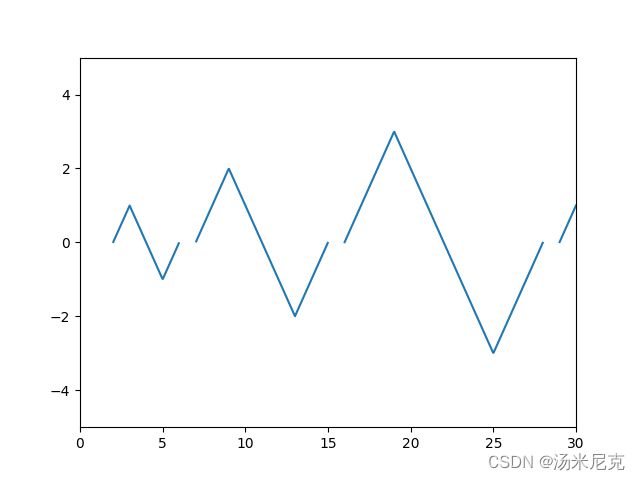
if 0 <= rel_dot < top: #分段函数
return rel_dot
elif top <= rel_dot < 3 * top:
return -rel_dot + 2 * top
elif 3 * top <= rel_dot <= 4 * top:
return rel_dot - 4 * top
比赛的时候我就是在分段函数上写错了一点,满盘皆输!!
- 时间复杂度:纯公式 O(1)
源代码
from math import ceil, sqrt
# import numpy as np
# from matplotlib import pyplot as plt
def fun(x):
top= ceil((-3 + sqrt(1 + 8 * x)) / 4) #每个波形的顶点值
last_dot = top + 2 * (top - 1) * ((top - 1) + 1) #上一个波形的结束点
rel_dot = x - last_dot - 1 #在此波形中的相对位置
if 0 <= rel_dot < top: #分段函数
return rel_dot
elif top <= rel_dot < 3 * top:
return -rel_dot + 2 * top
elif 3 * top <= rel_dot <= 4 * top:
return rel_dot - 4 * top
q=int(input())
for i in range(q):
print(fun(int(input())))
# x=np.linspace(0,30, 1000)
# y = np.array([fun(each) for each in x]) #根据x计算各点函数值
# plt.figure()
# plt.plot(x, y)
# plt.ylim(-5,5) #限制y的范围
# plt.xlim(0,30) #限制x的范围
# plt.show()
待续…✌️