人工智能理论

来源：http://worthpen.top/#/home/blog?blog=pot-blog27.md

1 人工智能的基本理论

1.1 人工智能的含义

研究人工智能本质上是逐渐去除人类干预的一个过程。对于实现某种任务的程序, 其人类干预程序越低, 则说明在该任务方面的智能化程度越高。而设计一个这样的程序就需要了解该程序实现的功能。人工智能需要实现的功能有：
(1) 具有目标。具有目标才能知道如何去做，实际上，这是所有算法所共有的部分。
(2) 接受反馈。接受反馈是学习或者行为的重要手段，因此一个人工智能模型需要具有接受反馈的能力。有的反馈可能是与正确量的差值，如监督学习，有的反馈可能是环境给与的奖惩，如强化学习。
(3) 学习能力。可以根据反馈，不断调整自身参数或者增加信息，得到输出结果。

图1

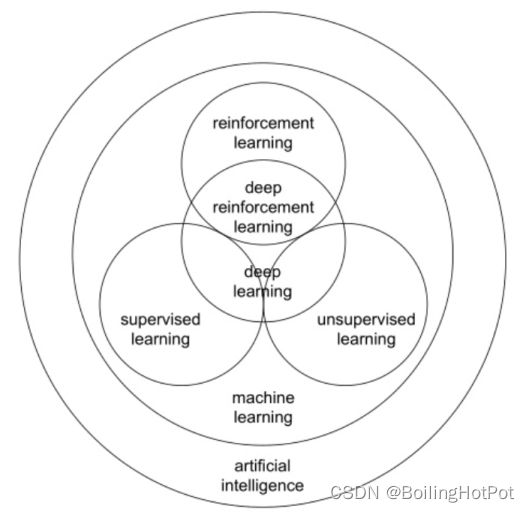
图2

1.2 人工智能可以解决哪些问题？

如图1所示。现实中存在诸多问题，有些问题不是数学问题，如今天吃什么？(不包含前提，环境等)。而根据哥德尔不完备定理，数学问题又存在不可计算的问题。图灵机可计算所有可计算问题(源于《论可计算数及其在判定性问题上的应用》)。可以完全建模图灵机即称为图灵完备，此处建模为图灵机的不一定是硬件，编程语言、人类语言都可以表达图灵机。当前计算机基于图灵机研究并且是图灵完备的。人工智能程序运行于计算机上，因此，人工智能只可以解决可计算问题。
然而，即使人工智能智能解决可计算问题，并不代表人工智能是不完善的。没有任何研究表明，人脑能解决图灵机不能解决的问题。

1.3 人工智能与图灵机的关系

首先，相对于图像，NLP是图灵完备模型，因为NLP可以描述图灵机。
但是，编程语言也具有图灵完备性，那为什么编程语言不是智能的呢？个人认为，编程语言所建模的图灵机不具备自主确定输入输出间映射的能力，需要依靠人工去实现状态转移的逻辑，即指令；而NLP的研究不仅仅是研究语言的表达，还研究了智能化，如何自发的进行对话，具有学习能力(符合1.1节)等。也就是说，一个完整的人工智能，既要可以建模图灵机(可以计算所有可计算问题)，又要具有自主确定输入输出映射的能力。

1.4 人工智能的基本解决方案

解决人工智能的三种大概方向有基于符号、基于联结和基于行为的方法。
基于符号主要是通过逻辑推理的方式实现人工智能。主要成果有专家系统等逻辑推断方法。
基于联结主要是通过仿生学模拟人脑，实现人工智能。主要成果有人工神经网络(ANN，Artificial Neural Network)，麦卡洛克-皮特斯模型(MP模型，是一种神经网络模型)，反向传播算法(BP，Back Propagation)等。图像识别的主流就是连接主义。
基于行为主要是通过模拟环境和行为的相互作用，实现人工智能。行为主义与符号主义和连接主义不同，不强调大脑（逻辑思维）的重要性，而是通过环境对行为的影响，来得到最优化的行为，然后将各种简单行为进行拼接，组成复杂行为，以实现最终的智能。主要成果有遗传算法，强化学习等。
行为主义和联结主义都是将大脑或者人类思维模式看作一个输入输出模型，经过外部数据的训练，得到一个黑盒式的系统。符号主义不在乎大脑的结构，而是解析大脑结构背后所代表的思维模式并将其复现。

1.5 反向传播算法的推导

https://blog.csdn.net/ft_sunshine/article/details/90221691

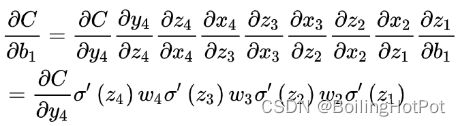
1.6 神经网络的可解释性的定义

我认为可解释性分为两点：一是对训练集和真实环境数据的差异评价问题，这导致了即使在训练集上寻到最优点，面对真实环境数据，依然无法保证百分之百对，或者在不是百分之百对的情况下，给出错误的原因，比如人会解释，因为这个耳朵有点像猫，但是不能确定，而神经网络最多能在输出时给出像猫的概率，不能给出是否时因为耳朵处不能确定，这也导致了无法进一步对错误进行提前预警，换句话说，就是你无法解释子式、参数和结果之间的联系，不具有稳定性；二是不能通过推导的方式给出最优的网络架构。

1.7 梯度消失和梯度爆炸

梯度消失和梯度爆炸是由反向传播过程中多次乘激活函数的导数和权重引起的。
在前向传播过程中, 传播的值为准确值, 虽然存在权重截断的情况, 但是最后一层不存在截断, 因此可以完整的提取特征并得到结果. 而在后向传播时, 误差受不同权重的影响, 有些位置的影响比较大或完全无影响, 但是由于其满足了激活函数的截断, 使得反向传播时激活函数的导数为0, 导致了反向传播计算对权重的导数为0, 即认为该权重不影响误差, 不需要改变, 实际上, 是需要改变的, 这就是梯度消失.
此外, 激活函数的导数意味着输入变化对于是否激活的影响, 导数越大, 更容易导致激活, 那么更容易导致误差变动, 那么误差的反向传播就更容易修改输入值. 在反向传播过程中, 由于多次跨过激活函数, 导数的计算乘了多次导数, 当导数不为1时, 神经网络前后的导数具有较大的差距. 这一过程计算出来的值是正确的, 其导数确实具有一定的差别. 由于导数确实存在一定的差别导致了不同的层对误差的反向传递也会有不同程度的反应, 当低层更容易激活时, 即导数大于1, 那么结果对于低层的变化就会更敏感, 导致了梯度爆炸; 当低层不容易激活时, 即导数小于1, 那么结果对底层的变化就会不敏感, 导致了梯度消失. 实际上, 最优的结果应该是结果对于高层和低层的敏感程度一样, 不单纯以来高层或者低层来实现拟合函数, 才可以实现更深的网络, 因此, 最优的应该是激活函数的导数等于1.
此外，如果权重的方差总是小与1，那么在反向传播过程中，多次乘权重，同样会导致梯度消失和爆炸。当然，这在非循环神经网络中并不严重，因为非循环网络各层间没有关系，因此，权重有时大于1，有时小于1，并不会造成梯度越来越大或越来越小的情况。而对于循环式的神经网络，由于是对于同一权重多次相乘，那么就会导致恒大于1或小于1的情况，随后出现梯度消失或梯度爆炸。

1.7.1 解决方案——梯度截断和固定梯度

对于比较大的梯度，可以使用梯度截断，即限制最大梯度为某值。实际上，梯度大并不一定梯度下降的步进大，如比较陡峭且短的低谷，很短的步进就会到达极小值，但是梯度却很大。因此，梯度的大小是无意义的，梯度截断也不会导致梯度失真。
那么为了保证梯度不会消失和爆炸，是否可以通过固定梯度，即对于比较大的梯度，缩小到某一固定值；对于比较小的梯度，放大到同一固定值呢？该方案是不行的，因为梯度阶段并不会导致步进过大，在恰当的学习率下（不考虑学习率），缩小并不会带来额外的风险。而对较小梯度进行放大时，不考虑学习率的修正，可能会导致步进过大，引起错过极小值。

1.8 激活函数

(1) 激活函数的输出需要满足0均值. 原因如下, 假定y=wx+b, 其中y为输出结果. 那么loss对w求导为
$$\frac{\mathrm{d}L}{\mathrm{d}w}=\frac{\mathrm{d}L}{\mathrm{d}y}\frac{\mathrm{d}y}{\mathrm{d}w}$$
激活函数存在某一偏向可以认为均为某一偏向. 因此, 假定激活函数均为正, 那么dy/dw为x, x为激活函数输出, 其均为正值. 那么loss对w求导则取决于结果, 而与特定的w无关, 这导致了如果存在两个w, 这两个权重的梯度是一样的, 无法实现一个权重增大, 另一个权重减小, 即约束性捆绑问题, 导致收敛缓慢.
(2) 激活函数的变化部分如果导数为1, 则不会有梯度消失和爆炸的问题
(3) 激活函数如果存在导数为0的地方, 则会在链式求导过程中出现乘0导致梯度消失.
(4) 单纯满足以上三个条件并不是有一个好的激活函数, 一个激活函数最重要的是非线性特性, 只有优秀的非线性特性才会具有更好的过拟合能力

1.9 梯度下降的步进问题

梯度下降的步进受学习率和梯度大小的影响，由1.14.1可知，梯度大小和应该有的步进无实际意义上的联系，此外，通过放缩梯度来实现步进的调整可能导致步进过大的问题。因此，假设梯度爆炸和梯度消失已经解决的前提下，应当通过调整学习率来决定梯度下降的步进。

1.10 神经网络的本质

神经网络的本质就是通过改变参数拟合数据集和数据集背后隐含的模型. 而隐模型的拟合程度则代表了泛化性. 对数据集的拟合和泛化性存在一定的联系和矛盾. 提高数据集的拟合程度可能会导致过拟合, 降低泛化性; 但过度降低对数据集的拟合程度可能同样不能很好的拟合隐模型. 此外, 通过降低对数据集的拟合并通过新数据进行诱导, 可能更好的拟合隐模型.

1.11 交叉熵原理

在信息理论中，相对熵是用来度量使用基于Q的编码来编码来P的样本平均所需的额外的比特个数, 其中Q表示预测分布或者理论分布, P表示真实分布. 因此, 相对熵虽然可以刻画两个概率的差异, 但是确实有先后顺序的.
https://blog.csdn.net/b1055077005/article/details/100152102

1.12 回归和分类的区别

回归得到的是一个结果, 不存在其他的候选选项, 错误的程度依照和真实结果的距离来判定. 而分类的结果是选择, 这些选择之间有不同的可能性. 人类的视觉跟踪等功能均是分类, 同时, 回归问题已经有了较好的解决方案, 因此与人工智能相关的问题是如果做好分类.

1.13 模型大小对性能的影响

1.13.1 Bias-Variance Tradeoff（权衡偏差与方差）

机器学习中的偏差和方差共同组成了最终的误差, 如图所示.

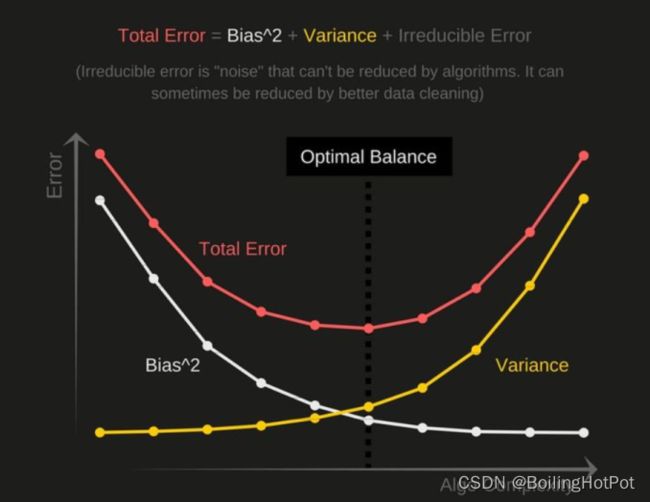
其中, 当模型复杂度较低时, 无法对任何结果进行预测, 就会造成偏差比较大的情况. 而当模型复杂度高时, 可以对某些结果进行低偏差的进行预测, 但是对于某些结果完全无法预测, 即过拟合现象, 只拟合部分数据, 就会造成高方差的情况.
https://zhuanlan.zhihu.com/p/142047021

1.13.2 大模型对于性能的提升

即使不使用权重正则, 同样会出现双下降（Double Descent）曲线
https://www.zhihu.com/question/434846017/answer/1651711327

1.14 神经网络模型

1.14.1 全连接网络

1.14.2 卷积神经网络

1.14.3 循环神经网络

循环神经网络用于提取序列特征和序列特征变换。在实体识别中，先用RNN提取输入序列的特征，再用全连接层进行分类；在翻译任务中，先用一个RNN提取输入序列的特征，再用另一个RNN转化输入序列为输出序列。翻译任务中不能只使用一个RNN，因为这样会导致输出的较前的单词只能基于输入的较前的单词。

1.14.4 对抗生成网络

对抗生成网络看似是无标签的(只需要一些图片, 而不需要具体分类), 实际上是有标签的. 因为风格迁移任务本身就不需要标签, 所以对抗生成网络看起来没有标签. 对抗生成本质上是一种生成网络, 生成的结果和理想结果的高层特征相同, 如果生成源是噪音, 理想结果为图片, 那么表现就是无标签; 如果生成源是图片, 理想结果也是图片, 那么表现就是有标签.

1.14.4.1 和UNet的区别

对抗生成网络和UNet都是生成网络, 两者都是根据一个高层抽象的特征生成结果. 其实, UNet和生成对抗网络在生成过程中是相同的, 两者的区别主要体现在如何利用标签, 即训练目的. UNet最后生成的结果需要和标签值一模一样, 而对抗生成网络生成的结果只需要让分类器分辨不出来即可. 分类器分辨是通过图片的高层特征来区分的, 因此, 让分类器分辨不出只需要两者的高层特征相同, 细节方面可以存在不同的地方.
两者利用标签的差异最后导致了, UNet是为了让生成的图细节和标签相同, 生成对抗网络是为了让生成的图高层特征和标签相同.

1.14.4.2 和卷积神经网络的区别

两者都是学习数据的映射. 卷积神经网络学习低层到高层特征的映射, 输入原图, 生成高层特征(是分布中的某点). 对抗生成网络学习高层到低层特征的映射, 输入噪声, 生成低层特征(实际上就是原图).
两者的训练目的也不一样, 卷积神经网络是为了让与标签(高层特征)相同, 对抗生成网络是为了让生成的结果的高层特征和标签的高层特征相同, 其中形成生成结果的高层特征的过程可以用卷积神经网络, 这里就是利用正向的卷积神经网络去得到反向的生成模型.

1.14.5 Transformer图解

https://blog.csdn.net/longxinchen_ml/article/details/86533005
transformer和RNN的主要区别在于特征提取部分，解码器部分使用的同样是RNN结构。因此，transformer最大的区别在于全局的特征提取。CNN是局部的特征提取，RNN是序列的特征提取。此外，transformer还用到了动态网络技术、迁移学习技术（用于保证全局的无归纳偏置的学习）。

1.14.6 图神经网络

https://www.zhihu.com/zvideo/1319699425372344320

1.15 学习方法

1.15.1 迁移学习

One/zero-shot learning分别指的是一次学习和零次学习。这两种学习是迁移学习下的两种极端情况。我们可以学习到一个映射，如果这个映射足够好的话，我们就可以处理没有看到的类了。比如，我们在训练时没有看见过狮子的图像，但是我们可以用这个映射得到狮子的特征。一个好的狮子特征，可能就和猫，老虎等等比较接近，和汽车，飞机比较远离。

1.15.2 强化学习

https://www.cnblogs.com/pinard/category/1254674.html

1.15.3 小样本学习

小样本学习的一个重要方法就是扩充数据集, 如果只有很少的样本, 那么随意的分类都可以将小样本进行好的分割, 然而只分割了小样本, 可能带来错误分割了ground truth. 因此, 可以在小样本的附近进行采样, 扩充样本, 采样的方式可以根据相似的类的均值的方差来采样, 按照高斯分布. 这样就可以扩充相对真实的样本. (refer to :Free Lunch for Few-shot Learning: Distribution Calibration.)
然而, 小样本学习实际上只是一个伪命题, 真实世界中并不存在小样本, 人的感知可以通过少量样本去学习, 这是由于人已经接受了世界上其他类的大量样本, 进行迁移学习, 最后可以通过少量样本去学习. 而第一段的方法是设计固定的流程, 完成大量样本的学习, 这与人工智能端到端自动化的思想背离. 第一段的方法可以看作是基于符号的AI, 但是有时候世界千变万化, 固定的流程并不能实现完全的自动化.

1.15.4 半监督学习

半监督学习是数据集中一部分有标签, 一部分无标签, 学习目标是在对无标签数据学习后, 可以提升仅有有标签数据学习的精度. 半监督学习有两种方案, 一种是基于熵最小原理, 一种是基于一致性原理. 熵最小原理是指通过优化让无标签数据的预测结果更加倾向于高置信度, 一致性原理是指让无标签数据的预测结果在加入噪声后变化量尽可能小.

1.15.5 增量学习

在模型已经训练完毕后，增加新数据进行训练，并且保证不遗忘旧数据。目前有基于正则化的方法（一边对新数据进行拟合，一边对新数据输入旧网络的输出进行拟合，类似于蒸馏学习）、保存代表性的旧数据以进行有放回的训练、扩充网络。
个人认为，比较合理且符合生理学的方法为保存旧数据进行有放回训练，类似于人做梦时会随机回忆过去来进行训练。可以通过生成模型来保存旧数据。

1.16 数据白化

对矢量数据进行变换，使得各轴不相关

1.17 神经网络相关的名词解释

全连接层：仅表示一层的结构
多层感知机：多个全连接层构成的网络
神经网络：总称。可以表示多层感知机，也可以表示卷积构成的网络，或者其他。
深度学习：深度学习是方法，而神经网络是模型。

1.18 样本不平衡

训练样本不平衡会导致模型倾向于将样本分类到大类的类别中。测试样本不平衡会导致评估结果倾向于大类别。训练模型就像是让一个人跑步，裁判来评判跑的如何，训练样本影响跑的方向，模型沿着预设方向带有一定的方向波动跑，测试样本影响如何评价，会在波动的方位内选择最好的结果。
训练样本不平衡使得小类中分类正确的样本变错误，大类中分类错误变正确，这在测试集中总是相对于平衡时按照比例进行变化的，而测试集的类别不平衡与该比例共同作用，得到具体的变化数量，假设测试集合为9：1，变化比例为0.2：0.1，则此时测试结果变动的真实比例为1.8：0.1，当真实比例为1：1时，评价的模型为最优。当然，训练集导致的变化比例是有限的，可能最终不会到达真实比例1：1。
改变分类阈值实际上改变了流动的比例，是有效的。
实验结果如图所示：

类别为1的样本数为25198，总样本数为50000

类别为1的样本数为5528，总样本数为50000

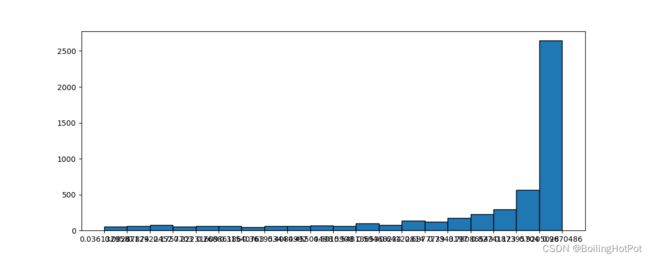
类别为1的样本数为5001，总样本数为10000

1.19 生物神经元与当前神经网络的优劣比较

以秀丽线虫为例，模拟秀丽线虫的神经元与M-P神经元模型的区别在于，生物神经元在细胞的不同位置具有不同的电动力学速率，这一特点通过多室模型进行实现；生物神经元的每个连接为不同类型的离子通道；生物神经元具有脉冲特性。以上不同使得302个生物神经元（秀丽线虫）就可以实现相比于M-P神经元模型更复杂的功能。

2 传统机器学习

2.1 似然率测试规则, 贝叶斯风险规则, 最大后验概率, 最短欧式距离规则

假设来自于不同模型的先验相同, 那么不同模型对于错误率的影响是等价的, 而贝叶斯代价的设置认为不同模型对于错误率的影响不同, 这导致了对于来自于不同模式的先验相同的模式识别问题的偏差从而降低了正确率. 而对于不同模式先验不相同的情况, 贝叶斯风险规则考虑了不同模型对于错误率的影响, 提升了正确率.
似然率测试规则可以认为是先验概率平均分布的情况下的最大后验概率规则. 当不同模式的先验概率不同时, 由于似然率测试规则仍然认为先验概率平均分布, 两者出现不同, 且最大后验概率更符合实际情况, 因此最大后验概率的结果更好. 此外, 由于贝叶斯风险规则同样考虑了先验分布, 因此其比最大后验概率的结果好.
最短欧式距离规则与似然率测试规则的结果相同. 这是由于最短欧式距离规则实际上是假设具有相同先验概率的最大后验概率, 因此其与似然率测试规则的结果相同.

2.2 似然估计、贝叶斯估计、最大后验估计

最大似然估计的目标函数是f(x|theta),贝叶斯估计的目标函数是f(x, theta)/f(x)。实际上，f(x)需要通过对f(x|theta)进行全部theta定义域的积分来求得，因此，很难计算。提出最大后验估计为f(x, theta)。相应的似然概率、贝叶斯概率、最大后验概率同理。

2.3 递推贝叶斯估计

递推贝叶斯估计就是在得到p(theta|x)后，将p(theta|x)视为p(theta)，带入贝叶斯估计中，使用新数据y，估计f(theta|y)/f(y)。可以一次性使用全部样本点实现贝叶斯估计，如果一次计算量太大，可以通过递推的方式减小计算量。

3 论文阅读记录

3.1 Elimination of All Bad Local Minima in DL

该论文貌似改善了最后的权重误差关系图, 使得最终的关系图中仅有一个极值点, 但是由于大量鞍点同样导致了不能搜索到全局最优点, 因此该论文目前来说意义不大.