红黑树的插入和删除详解
红黑树RB-tree
找了很多其他人的,红黑树的插入大部分都能理解,在删除部分有些博客很难理解进行,就自己写了一篇详细的,有问题欢迎请指出。
作为一种广泛应用的平衡二叉搜索树之一,需要我们有些清晰的了解
红黑树的结点增删改查效率非常优良,都为log(N),其应用十分广泛:
- Linux内核进程调度由红黑树管理进程控制块。
- Epoll用红黑树管理事件块。
- C++ STL中的map和set的底层实现。
STL相关RB-Tree代码编写请跳转:https://blog.csdn.net/qq_38223012/article/details/119656982
用于理解红黑树的生成演示网站:https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
规则
红黑树的规则(非常重要,必须牢记):
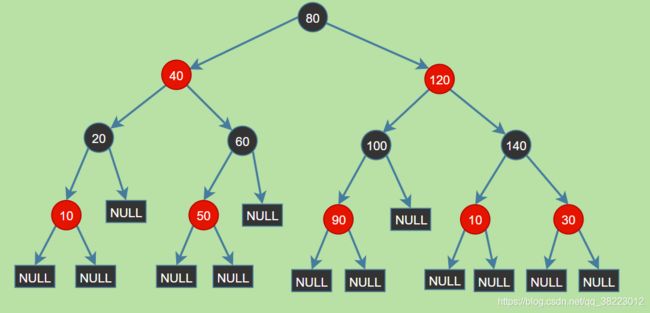
(1)每个结点或者是黑色,或者是红色。
(2)根结点是黑色。
(3)每个叶子结点(NIL或null)的黑结点。
(4)如果一个结点是红色的,则它的子结点必须是黑色的。
(5)任一结点至NULL(树尾端)的任何路径,所含之黑结点数必须相同。
注意默认事项:
如此可以得出结论:
- 根据规则4,新增结点必须为红;
- 根据规则3,新增结点之父结点必须为黑。
当新结点根据二叉搜索树的规则到达其插入点,却未能符合上述条件时,就必须调整颜色并旋转树形。
左右旋
红黑树的基本操作是添加、删除。在对红黑树进行添加或删除之后,红黑树就发生了变化,可能不满足红黑树的4条规则,也就不再是一颗红黑树了,而是一颗普通的树。而通过旋转,可以使这颗树重新成为红黑树。简单点说,旋转的目的是让树保持红黑树的特性。
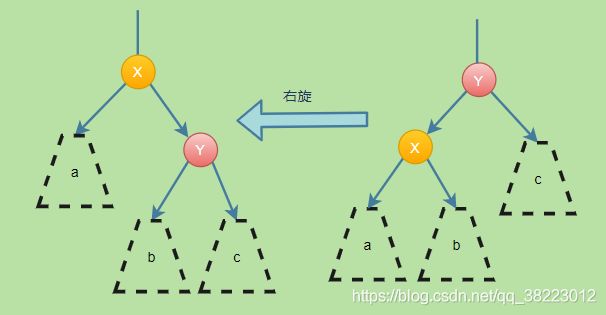
X、Y结点往左方向移动,X结点成为Y的左结点, Y的左子树成为X的右子树
X、Y结点往右方向移动,Y结点成为Y的右结点, X的右子树成为Y的左子树
红黑树插入
插入操作包括两部分工作:一查找插入的位置;二插入后自平衡。查找插入的父结点很简单,跟查找操作区别不大:
-
查找位置:查找到对应值,保持不变,结束当前查找,否则就是查找到对应位置结束当前查找。
-
插入后自平衡:插入结点为红色 ,插入结点的父结点(如果存在)为黑色结点时,红黑树的黑色平衡没被破坏,不需要做自平衡操作。如果插入结点的父结点为红色,不满足规则4,需要进行自平衡调整。
插入结点符号定义
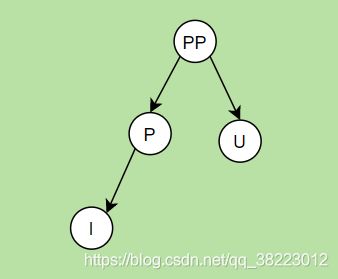
P:父亲结点
U:叔叔结点
I:插入结点
插入情景1:红黑树为空树
把插入结点作为根结点,并把结点设置为黑色。
插入情景2:插入结点的Key已存在
插入结点的Key已存在,更新当前结点的值并保持颜色不变
插入情景3:插入结点的父结点为黑结点
由于插入的结点是红色的,并不会影响红黑树的平衡,直接插入即可,无需做自平衡。
插入情景4:插入结点的父结点为红结点
平衡被破坏的四种情景:
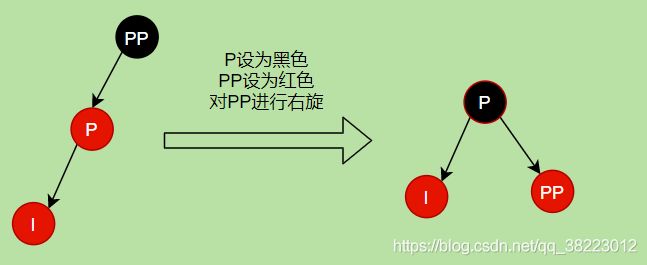
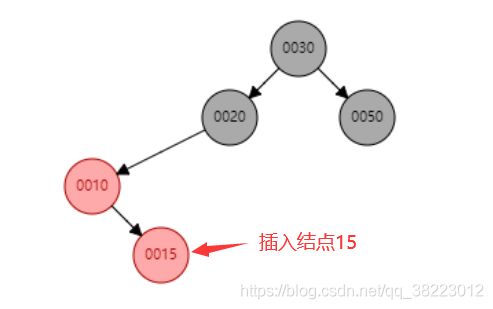
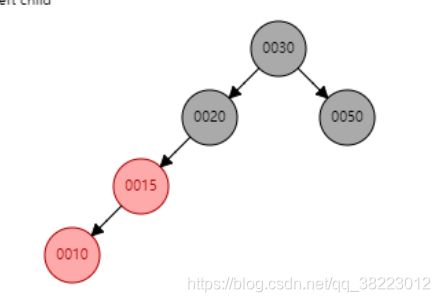
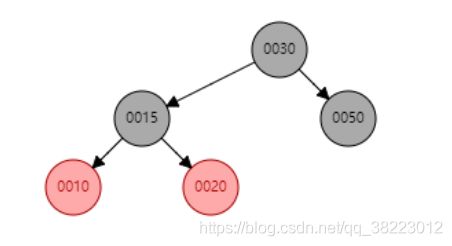
- 插入结点位于PP祖父结点的左子结点的左子树—左左----单旋-----右旋
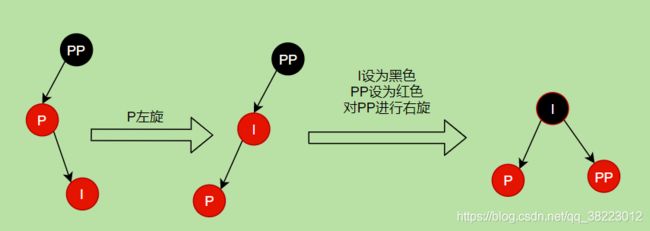
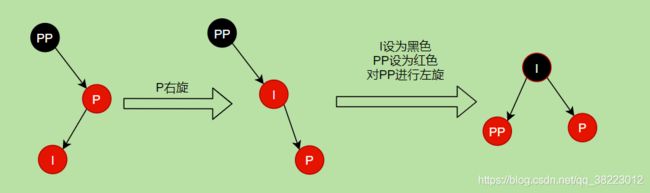
- 插入结点位于PP祖父结点的左子结点的右子树—左右----双旋-----左旋右旋
- 插入结点位于PP祖父结点的右子结点的左子树—右左----双旋-----右旋左旋
- 插入结点位于PP祖父结点的右子结点的右子树—右右----单旋-----左旋
- 插入情景4.1:叔叔结点存在并且为红结点
从红黑树规则4可以,祖父结点肯定为黑结点,因为不可以同时存在两个相连的红结点。那么此时该插入子树的红黑层数的情况是:黑红红。
不满足规则4,处理方式是把其改为:红黑红。之后又不满足规则1
将根节点变为黑色
- 插入情景4.2:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的左子结点
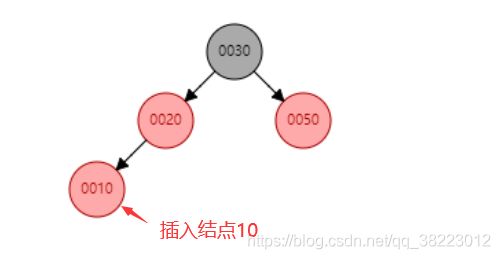
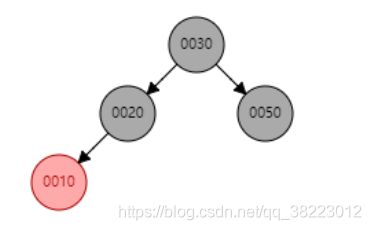
- 插入情景4.2.1:插入结点是其父结点的左子结点
案例情况:
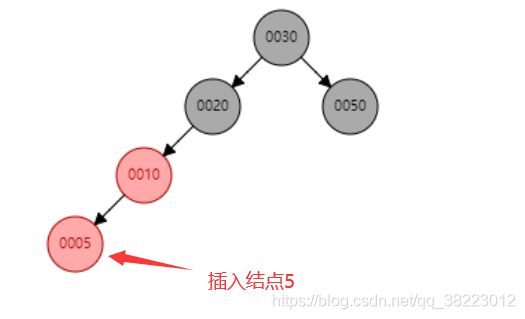
- 插入情景4.2.2:插入结点是其父结点的右子结点
不满足规则3,进行左旋
回到情景4.2.1
- 插入情景4.3:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的右子结点
这里只是和4.2进行对称镜像,上面理解了4.3也就很好理解了。
- 插入情景4.3.1:插入结点是其父结点的右子结点
- 插入情景4.3.2:插入结点是其父结点的左子结点
红黑树删除
红黑树的删除操作也包括两部分工作:一查找目标结点;二删除后自平衡。
查找目标结点显然可以复用查找操作,当不存在目标结点时,忽略本次操作;
当存在目标结点时,删除后就得做自平衡处理了。
二叉树删除结点找替换结点有3种情情景:
- 情景1:若删除结点无子结点,直接删除
- 情景2:若删除结点只有一个子结点,用子结点替换删除结点
- 情景3:若删除结点有两个子结点,用后继结点(大于删除结点的最小结点,也是删除结点的右子树的最左结点)替换删除结点,也可以用前继结点(小于删除结点的最大结点,也是删除结点的左子树的最右节点)
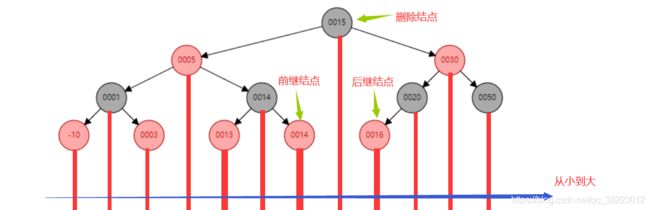
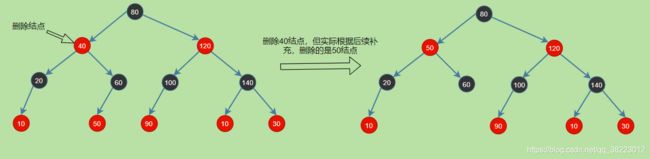
如图所示,你可以找前继结点替换,也就使用后继结点替换,两种都可以维持住搜索树的性质。
**重要的思路:**删除结点被替代后,在不考虑结点的键值的情况下,对于树来说,可以认为删除的是替换结点!
情景2:删除结点有唯一子节点,用子结点替换删除结点,如此删除结点就转化为删除子结点,若子节点没有子节点,则为情景1;若子结点有两个子结点,那么相当于转换为情景3,再自顶向下转换,总能转换为情景1。
情景3:删除结点用后继结点(肯定不存在左结点,如果存在就不是后继结点了),如果后继结点有右子结点,那么相当于转换为情景2,否则转为为情景1。
个人总结:删除结点后,首先是替换结点的移动,相当于把删除结点的值更新为替换结点,颜色保持为删除结点原本的颜色,然后删除替换结点,之后再进行自平衡处理。所以自平衡主要在于删除替换结点,之后去改变结点颜色,以满足红黑树规则。而替换结点最后总是在树末,要么只有一个叶子结点(情景2),要么没有叶子结点(情景1),所以只考虑删除树末结点的情景。
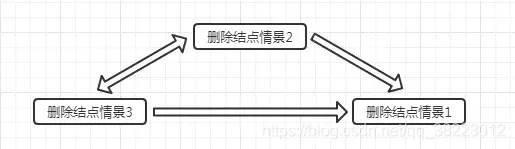
接下来开始3种删除情景的解决方式介绍,情景2,、3都可以转换为情景1,我们先解决简单的情景2、3,再去研究删除结点的重点情景1.
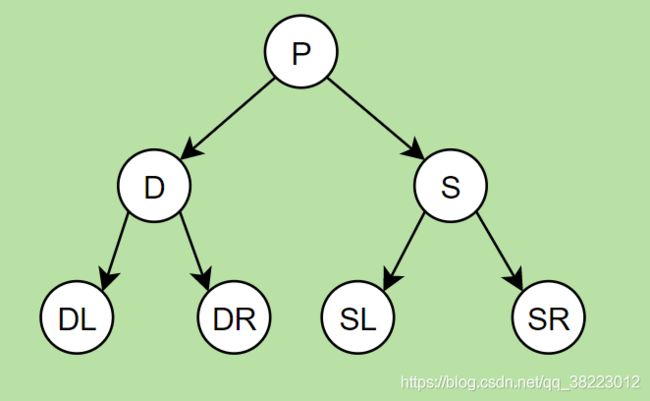
删除结点符号的规定
D:删除结点
DL:删除结点的左子结点
DR:删除结点的右子结点
P:删除结点的父节点
S:删除结点的兄弟结点
SL:删除结点的兄弟结点的左子结点
SR:删除结点的兄弟结点的右子结点
情景2:删除节点只有一个子节点
根据规则5,删除结点必定为黑,其子节点必定为红
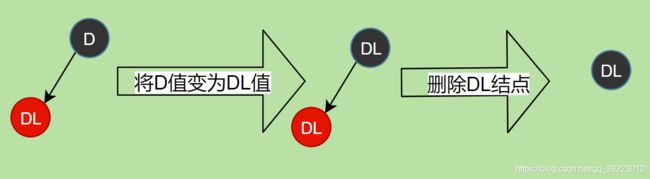
情景2.1:删除节点只有一个左子节点
- 将D的值变成DL的值
- 删除DL节点
情景2.2:删除节点只有一个右子节点
- 将D的值变成DR的值
- 删除DR节点
情景3:删除节点有两个子节点
- 将删除结点值替换成后续结点的值
- 删除结点变为删除后续结点,此时就相当于是情景1或2的情况
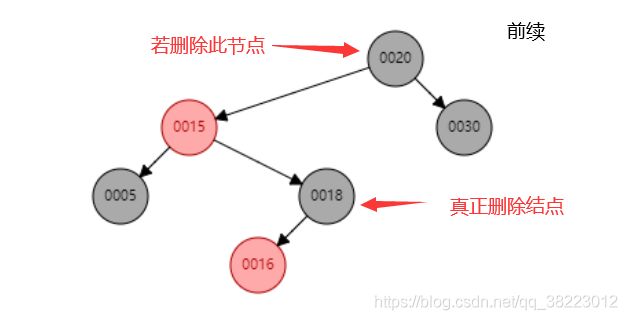
情景3—>情景2(前继结点):
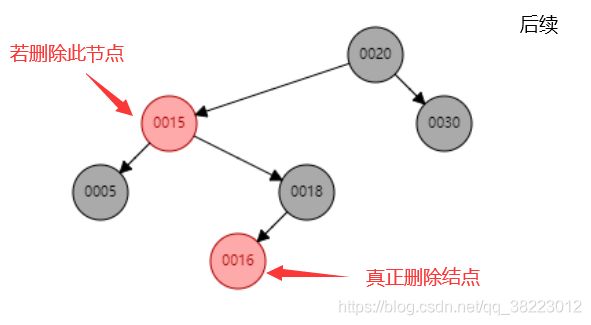
情景3—>情景1(后继结点):
注意:在情景3—>情景1时,这里根据方法又有不一样的情形
-
前续结点时:考虑D结点在P结点的右子树上
-
后续结点时:考虑D结点在P结点的左子树上
虽然两种方式结果一下,但是处理过程有区别,选一种就好,通常习惯以后续结点作为替换节点
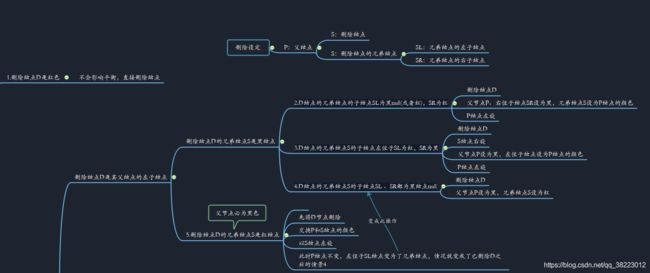
情景1:删除结点为叶子结点
这里只列出情景1,删除结点在左子树上的所有可能
删除情景1.1:D结点是红色结点
直接删除即可
删除情景1.2:D结点是黑结点
当D结点是黑色时,规则5被破坏,我们就不得不进行自平衡处理了。
D结点是其父结点的左子结点(或者情景3后继结点情况)
删除情景1.2.1:D结点的兄弟结点S是黑结点
这种情况下,一旦D结点被删除,P结点的左子树就右子树黑色结点数少1,P结点红色或者黑色都有可能,那两个侄子SL、SR要么为null,要么为红色。
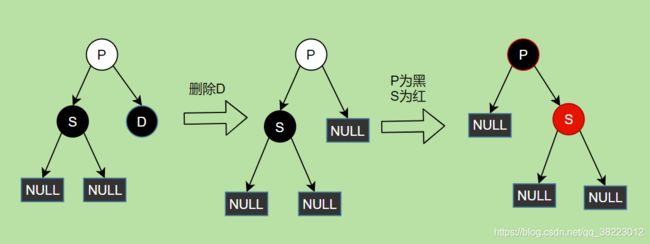
删除情景1.2.1.1:D结点的兄弟结点S的子结点SL 、SR都为黑结点null
- 删除结点D
- 父节点P设为黑,兄弟结点S设为红
如果P结点处,黑节点数以为N,此时P的左右子树方向,黑节点数都为N+2+(P )
转化以后,此时P的左右子树方向,黑节点数都为N+2,满足条件
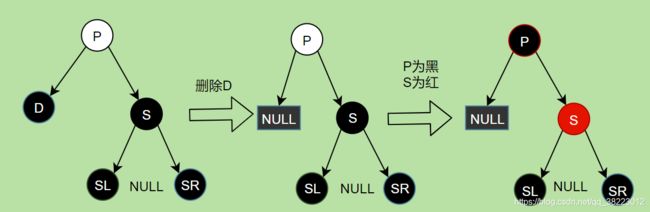
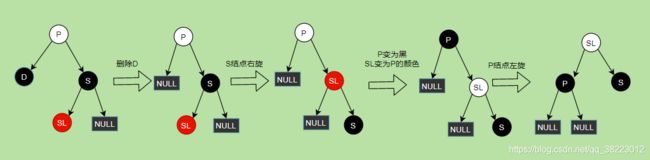
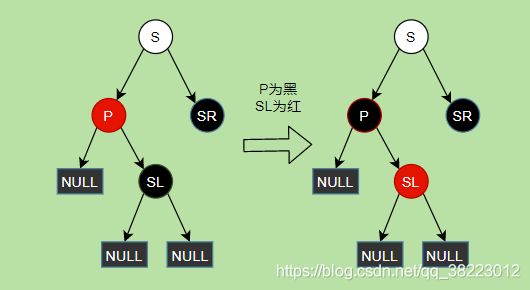
删除情景1.2.1.2:D结点的兄弟结点S的子结点SL为红,SR为黑null(或者红)
- 删除结点D
- S结点右旋
- 父节点P设为黑,左侄子结点设为P结点的颜色
- P结点左旋
如果P结点处,黑节点数以为N,此时P的左右子树方向,黑节点数都为N+2+(P )
转化以后,此时SL的左右子树方向,黑节点数都为N+2+(SL),满足条件
如果右侄子SR结点也为红色,处理方式是一样的,结果也是一样的,并不影响红黑树平衡,所以右侄子结点SR颜色可以随意。
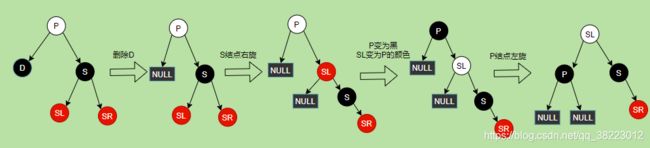
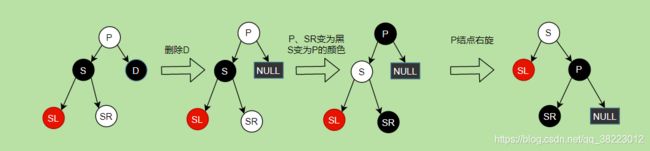
删除情景1.2.1.3:D结点的兄弟结点的子结点SL为黑null(或者红),SR为红
- 删除结点D
- 父节点P、右侄子结点SR设为黑,兄弟结点S设为P结点的颜色
- P结点左旋
如果P结点处,黑节点数以为N,此时P的左右子树方向,黑节点数都为N+2+(P )
转化以后,此时S的左右子树方向,黑节点数都为N+2+(S),满足条件
如果左侄子SL结点也为红色,处理方式是一样的,结果也是一样的,也不影响红黑树平衡,所以左侄子结点SL颜色可以随意。
这里可以稍微总结一下:如果兄弟结点S为黑色,有两种路线可以走,任选其一就好
第一种:
- 先判断右侄子SR,是否为红色?
- 是,1.2.1.3处理,不是,判断左侄子SL是否为红色?
- 是,1.2.1.2处理,不是,1.2.1.1处理
第二种:
- 先判断左侄子SL,是否为红色?
- 是,1.2.1.2处理,不是,判断右侄子SR是否为红色?
- 是,1.2.1.3处理,不是,1.2.1.1处理
无论那种都能实现红黑树的平衡,感觉1.2.1.3的处理步骤少一些,就选第一种。
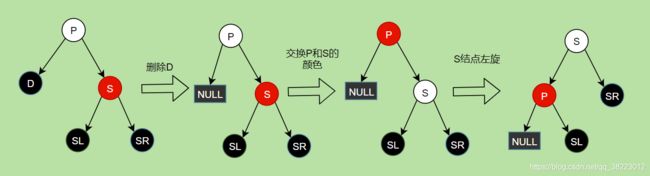
删除情景1.2.2:D结点的兄弟结点S是红结点,D的左侄子SL和右侄子SR都为黑色
- 先将D节点删除
- 交换P和S结点的颜色
- 以S结点左旋
- 此时P结点不变,左侄子SL结点变为了兄弟结点,情况就变成了已删除D之后的情景1.2.1.1
如果P结点处,黑节点数以为N,此时P的左右子树方向,黑节点数都为N+2+(P )
转化以后,此时S的左右子树方向,黑节点数都为N+2+(S),满足条件
D结点是其父结点的右子结点(或者情景3前续结点情况)
右边的操作方向相反,就是做一个镜像处理不做过多说明了
删除情景1.2.3:D结点的兄弟结点S是黑结点
删除情景1.2.3.1:D结点的兄弟结点S的子结点SL 、SR都为黑结点null
- 删除结点D
- 父节点P设为黑,兄弟结点S设为红
如果P结点处,黑节点数以为N,此时P的左右子树方向,黑节点数都为N+2+(P )
转化以后,此时P的左右子树方向,黑节点数都为N+2,满足条件
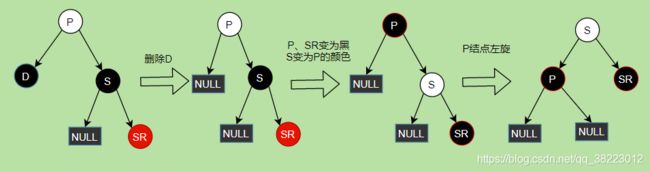
删除情景1.2.3.2:D结点的兄弟结点S的子结点SL为红,SR为黑null(或者红)
- 删除结点D
- 父节点P、右侄子结点SR设为黑,兄弟结点S设为P结点的颜色
- P结点右旋
如果P结点处,黑节点数以为N,此时P的左右子树方向,黑节点数都为N+2+( P)
转化以后,此时S的左右子树方向,黑节点数都为N+2+(S),满足条件
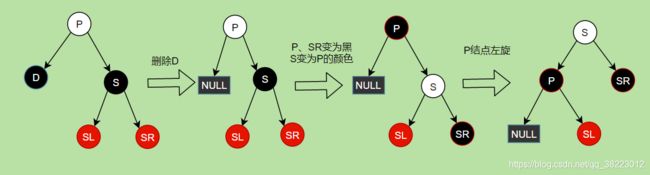
删除情景1.2.3.3:D结点的兄弟结点的子结点SL为黑null(或者红),SR为红
- 删除结点D
- S结点左旋
- 父节点P设为黑,左侄子结点设为P结点的颜色
- P结点右旋
如果P结点处,黑节点数以为N,此时P的左右子树方向,黑节点数都为N+2+(P )
转化以后,此时S的左右子树方向,黑节点数都为N+2+(SR),满足条件
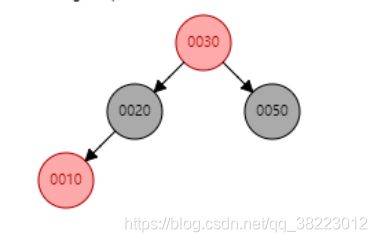
删除情景1.2.4:D结点的兄弟结点S是红结点,D的左侄子SL和右侄子SR都为黑色
- 先将D节点删除
- 交换P和S结点的颜色
- 以P结点右旋
- 此时P结点不变,右侄子SR结点变为了兄弟结点,情况就变成了已删除D之后的情景1.2.3.1