leetcode每日一题复盘(11.13~11.19)
leetcode 435 无重叠区间
本题和射气球最小箭数大同小异,但是这一题没做出来,难就难在题目如何理解:移除区间最小数量,使剩下的区间不重叠
那么本质上就是求最少有多少个重叠区间,把重叠区间去掉剩下的区间即不重叠
这里有两种做法,不同在于数组的排序方式,也就是获取重叠区间的方法不一样
第一种是以结束下标为依据,小的排在前面,用其他区间的开始下标和结束下标进行比较,如果开始下标小于结束下标,说明两个区间重叠,当开始下标大于等于结束下标时说明有新的非重叠区间,数量+1
结果以两者之差返回
个人比较偏向于第二种方法,直接统计重叠的区间数量
第二种方法以开始区间为排序依据,结束下标小的排在前面,用结束下标和开始下标进行比较,如果结束下标大于开始下标说明区间重叠,并更新结束下标的值,否则说明区间不重叠
两种方法大同小异,比较的方法都相同,不同在于排序的方法和统计的目标
leetcode 56 合并区间
如果之前做过重叠区间之类的题目,这一题很值得去做一下
做法和重叠区间的题很类似,都是排序,遍历选出重叠区间,这一题难在题目理解,合并过后区间是会增长的,这也是和一般的重叠问题不同的地方
举例:[0,2],[1,4],[3,5]
重叠问题时有两个重叠区间,合并问题时只有一个区间
不同点在于每一次在范围内的遍历都会更新最右边的值
理解了这一点后,其他的都不难了就是在右边界内的就更新右边界的最大值,超过右边界则加入结果集中,重新设定边界值,重复上面操作即可
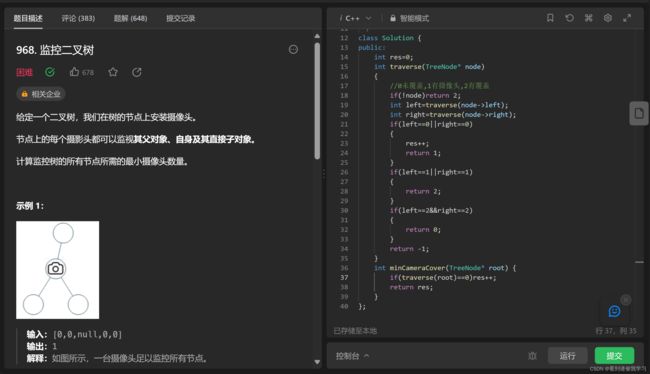
leetcode 968 监控二叉树
想不出来,连用哪种遍历方式都不知道,果断点开题解哈哈哈
写完之后感觉难就难在分辨哪种情况摄像头是最少的,遍历方式是哪种,如何表示无有摄像头的状态等
这里从头到尾重新分析一下这道题的全过程:
首先题目要求摄像头最少,那么就需要思考什么时候摄像头是最少的,覆盖的多自然用的就少,什么时候覆盖率低呢?在叶子节点放摄像头的时候最低,空节点浪费了摄像头的覆盖范围,因此叶子节点不放摄像头时摄像头最少
知道了叶子节点不放摄像头,怎么保证叶子不放摄像头呢?选前序遍历还是后序遍历?这里已经可以让人思考好一会了
关于选前序还是后序的问题,我们需要关注到根节点,根节点如果放摄像头也会造成范围的浪费,因此我们要尽可能不在根节点放摄像头。前序遍历必然会在根节点放摄像头,因此我们选择后序遍历从底向上设置摄像头
想到后序遍历但如何保证叶子节点不放摄像头的问题依然没有解决,我们先放一放,先对树的情况进行分类
树节点的状态大致可分成三种情况:
覆盖
没覆盖
有摄像头
为什么没有无摄像头这个情况呢,其实是可以有的,但是我们为了简化把第四种情况删去了,因为无摄像头的情况依然要判断是否覆盖,可以说第一第二种情况已经包含无摄像头的情况了
而有摄像头是必须的,因为需要以此来确定返回值
三种情况可以根据左右子树进行细分:
覆盖:1个,2个
未覆盖:1个,2个
有摄像头
其中覆盖一个和未覆盖一个其实是同一种情况,当覆盖2个和有摄像头的时候可以不放摄像头,其他情况都需要放摄像头
在代码里我们用整数0,1,2分别代表节点的状态,通过返回值传递\获取节点状态,这是一个很关键的点
回到保证叶子节点不放摄像头的问题,知道什么时候放摄像头后我们就可以对应下手了,两个子树都覆盖的时候就不放摄像头,那么我们把空节点也当作覆盖即可
到这里这道题的难点应该是讲完了,理解倒是不难,但是到自己独立做的时候能做到思路这么清晰吗,还是需要不断练习
leetcode 70 爬楼梯
到现在也刷了一百多道题了,最近打算把算法放一放重心放到开发上面去,以后可能就没有一周一篇复盘文章了
初学动态规划,动态规划一言蔽之就是根据上一个状态推导出下一个状态
这里和贪心区分一下,贪心是局部选最优,不会根据上一次的状态作选择
动态规划五部曲:
1.确定dp数组和数组下标i的意义
2.确定推导公式(也就是状态是如何更新的)
3.初始化dp数组
4.确定如何遍历dp数组
5.推导dp数组
根据这五部曲去思考问题,而不是盲目去写,在写之前先想清楚这几件事再下手
爬楼梯这一题一开始想的是递归,结果超时了,算是给自己复习一下递归三部曲吧
一开始真没想到怎么设计dp数组,总想着记录一共爬了多少阶,忽略了动态规划中很重要的一个东西,就是状态,如何确定状态才是关键,这里求有几种方法能达到n阶,最重要的状态就是有几种方法而不是爬了多少阶,这个就是关键,选择错了状态一切都难写了
求到达n阶的方法,也即是求到达n-1阶和n-2阶的方法之和!因为到达n-1和n-2就可以到达n,明白了这个就可以根据n-1和n-2的状态推出n的状态了,这也就得出了我们的递推公式f(n)=f(n-1)+f(n-2);
明白了这一点这道题就不难了,就是简单的求斐波那契数列