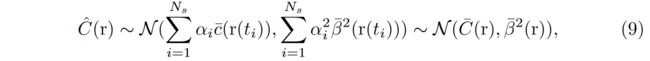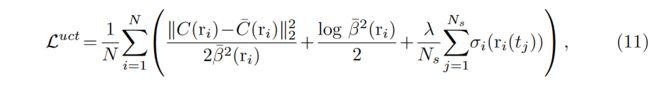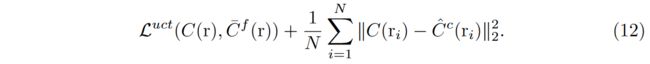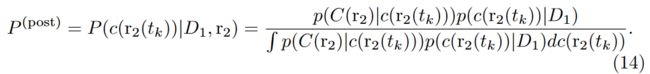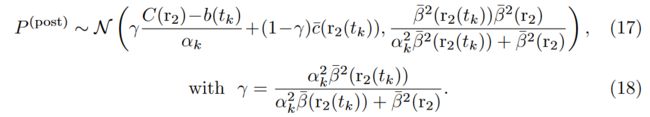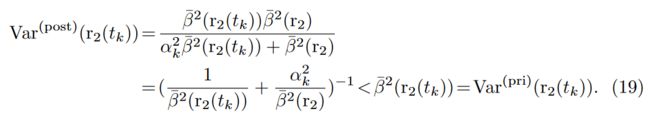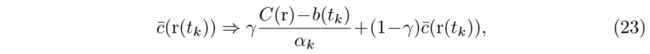【论文阅读】ActiveNeRF：通过不确定性估计候选新视图

Abstract

Recently, Neural Radiance Fields (NeRF) has shown promising performances on reconstructing 3D scenes and synthesizing novel views from a sparse set of 2D images. Albeit effective, the performance of NeRF is highly influenced by the quality of training samples. With limited posed images from the scene, NeRF fails to generalize well to novel views and may collapse to trivial solutions in unobserved regions. This makes NeRF impractical under resource-constrained scenarios. In this paper, we present a novel learning framework, ActiveNeRF, aiming to model a 3D scene with a constrained input budget. Specifically, we first incorporate uncertainty estimation into a NeRF model, which ensures robustness under few observations and provides an interpretation of how NeRF understands the scene. On this basis, we propose to supplement the existing training set with newly captured samples based on an active learning scheme. By evaluating the reduction of uncertainty given new inputs, we select the samples that bring the most information gain. In this way, the quality of novel view synthesis can be improved with minimal additional resources. Extensive experiments validate the performance of our model on both realistic and synthetic scenes, especially with scarcer training data. Code will be released at https://github.com/LeapLabTHU/ActiveNeRF.

最近，神经辐射场 (NeRF) 在重建 3D 场景和从一组稀疏的 2D 图像中合成新颖的视图方面表现出了良好的性能。尽管有效，但 NeRF 的性能很大程度上受训练样本质量的影响。由于场景中的姿势图像有限，NeRF 无法很好地推广到新颖的视图，并且可能会在未观察到的区域中崩溃为破碎结果。这使得 NeRF 在资源受限的情况下不切实际。在本文中，我们提出了一种新颖的学习框架 ActiveNeRF，旨在以有限的输入对 3D 场景进行建模。具体来说，我们首先将不确定性估计纳入 NeRF 模型中，这确保了少视角下的鲁棒性，并提供了 NeRF 如何理解场景的解释。在此基础上，我们建议基于主动学习方案用新捕获的样本来补充现有的训练集。通过评估给定新输入的不确定性的减少，我们选择带来最大信息增益的样本。通过这种方式，可以用最少的额外资源来提高新颖视图合成的质量。大量的实验验证了我们的模型在现实场景和合成场景上的性能，特别是在训练数据较少的情况下。代码将在 https://github.com/LeapLabTHU/ActiveNeRF 发布。

1 Introduction

Despite its success in synthesizing high-quality images, the learning scheme for a NeRF model puts forward higher demands on the training data. First, NeRF usually requires a large number of posed images and is proved to generalize poorly with limited inputs [36]. Second, it takes a whole observation in the scene to train a well-generalized NeRF. As illustrated in Figure 2, if we remove observations of a particular part in the scene, NeRF fails to model the region and tends to collapse (e.g., predicting zero density everywhere in the scene) instead of performing reasonable predictions. This poses challenges under real-world applications such as robot localization and mapping, where capturing training data can be costly, and perception of the entire scene is required [23,11,31].

尽管 NeRF 模型在合成高质量图像方面取得了成功，但其学习方案对训练数据提出了更高的要求。首先，NeRF 通常需要大量的位姿已知图像，并且被证明在输入有限的情况下泛化能力很差 [36]。其次，需要对场景进行整体观察来训练泛化良好的 NeRF。如图 2 所示，如果我们删除场景中特定部分的观测，NeRF 无法对该区域进行建模，并且往往会崩溃（例如，预测场景中各处的密度为零），而不是执行合理的预测。这在机器人定位和地图绘制等现实应用中提出了挑战，其中捕获训练数据的成本可能很高，并且需要感知整个场景[23,11,31]。

图 2. 部分视角的 NeRF 新颖视图合成。这些模型使用 10 张位姿已知图像进行训练，其中从训练集中删除了左侧的观测。虽然我们的模型仍然可以生成相当好的合成结果，但原始 NeRF 显示出很大的错误或完全无法生成有意义的内容。

In this paper, we focus on the context with constrained input image budget and attempt to address these limitations by leveraging the training data in the most efficient manner. As shown in Figure 1, we first introduce uncertainty estimation into the NeRF framework by modeling the radiance values of each location as a Gaussian distribution. This imposes the model to provide larger variances in the unobserved region instead of collapsing to a trivial solution. On this basis, we resort to the inspiration from active learning and propose to capture the most informative inputs as supplementary to the current training data. Specifically, given a hypothetical new input, we analyze the posterior distribution of the whole scene through Bayesian estimation, and use the subtraction of the variance from prior to posterior distribution as the information gain. This finally serves as the criterion for capturing new inputs, and thus raises the quality of synthesized views with minimal additional resources. Extensive experiments show that NeRF with uncertainty estimation achieves better performances on novel view synthesis, especially with scarce training data.

在本文中，我们关注输入图像受限的背景，并尝试通过以最有效的方式利用训练数据来解决。如图 1 所示，我们首先通过将每个位置的辐射值建模为高斯分布，将不确定性估计引入 NeRF 框架中。这迫使模型在未观察到的区域提供更大的方差，而不是崩溃为破碎结果。在此基础上，我们基于主动学习的灵感，并建议捕获信息量最大的输入作为当前训练数据的补充。具体来说，给定一个假设的新输入，我们通过贝叶斯估计来分析整个场景的后验分布，并将先验分布与后验分布的方差相减作为信息增益。这最终作为捕获新输入的标准，从而以最少的额外资源提高合成视图的质量。大量实验表明，具有不确定性估计的 NeRF 在新视图合成方面取得了更好的性能，尤其是在训练数据稀缺的情况下。
Our proposed framework based on active learning, dubbed ActiveNeRF, also shows superior performances on both synthetic and realistic scenes, and outperforms several heuristic baselines.

我们提出的基于主动学习的框架（称为 ActiveNeRF）在合成场景和现实场景上也显示出卓越的性能，并且优于多个启发式基线模型。

图 1. ActiveNeRF：我们提出了一个灵活的学习框架，该框架基于主动学习方案，利用新捕获的样本主动扩展现有的训练集。ActiveNeRF 将不确定性估计纳入 NeRF 模型，并评估在未观察到的新视图中场景不确定性的减少情况。通过选择能带来最大信息增益的视图，可以用最少的额外资源提高新视图合成的质量。

3 Background

4 NeRF with Uncertainty Estimation

In this paper, we focus on the context in some real-world applications, where the number of training data is within a limited budget. It has been proved in existing research [36] that NeRF fails to generalize well from one or few input views. If with incomplete scene observation, the original NeRF framework tends to collapse to trivial solutions by predicting the volume density as 0 for the unobserved regions. As a remedy, we propose to model the emitted radiance value of each location in the scene as a Gaussian distribution instead of a single value. The predicted variance can serve as the reflection of the aleatoric uncertainty concerning a certain location. Through this, the model is imposed to provide larger variances in the unobserved region instead of collapsing to the trivial solution.

在本文中，我们将重点关注一些实际应用中的背景情况，即训练数据的数量有限的情况下。现有研究[36]已经证明，NeRF 无法从一个或几个输入视图中很好地泛化。如果场景观察不完整，原始 NeRF 框架往往会通过将未观察区域的体积密度预测为 0 来崩溃为破碎结果。作为补救措施，我们建议将场景中每个位置的辐射值建模为高斯分布而不是单个值。预测方差可以反映某个位置的任意不确定性。通过这种方式，模型可以在未观察到的区域提供更大的方差，而不是崩溃到破碎结果。
Specifically, we define the radiance color of a location $r(t)$ follows a Gaussian distribution parameterized by mean $\overline{c}(r(t))$ and variance ${\overline{\beta }}^2(r(t))$. Following previous researches in Bayesian neural networks, we take the model output as the mean, and add an additional branch to the MLP network in Eq.(1) to model the variance as follows:

具体来说，我们定义某个位置的辐射颜色 $r(t)$ 为高斯分布，参数为均值 $\overline{c}(r(t))$和方差 ${\overline{\beta }}^2(r(t))$。根据贝叶斯神经网络的前人研究，我们将模型输出作为均值，并在公式（1）中的 MLP 网络中添加一个额外的分支来建立方差模型，如下所示：

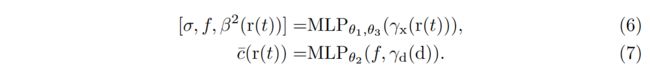
Softplus function is further adopted to produce a validate variance value:

进一步采用 Softplus 函数来产生验证方差值：

where ${\beta }_0^2$ ensures a minimum variance for all the locations.

其中 ${\beta }_0^2$ 确保所有位置的方差最小。

In the rendering process, the new neural radiance field with uncertainty can be similarly performed through volume rendering. As we have mentioned in Sec. 3, the design paradigm in the NeRF framework provides two valuable prerequisites. (1) The radiance color of a particular position is only affected by its own 3D coordinates, which makes the distribution of different positions independent from each other. (2) Volume rendering can be approximated as linear combination of sampled points along the ray. On this basis, if we denote the Gaussian distribution of a position at $r(t)$ as $c(r(t))\sim N(\overline{c}(r(t)),{\overline{\beta }}^2(r(t)))$, the rendered value along this ray naturally follows Gaussian distribution:

在渲染过程中，新的具有不确定性的神经辐射场可以通过体渲染类似地进行。正如我们在第 3 节中提到的，NeRF框架中的设计范式提供了两个有价值的先决条件。 (1)特定位置的辐射颜色仅受其自身3D坐标的影响，这使得不同位置的分布相互独立。 (2)体绘制可以近似为沿射线采样点的线性组合。在此基础上，如果我们把位于 $r(t)$ 处的位置的高斯分布记为 $c(r(t))\sim N(\overline{c}(r(t)),{\overline{\beta }}^2(r(t)))$ ，那么沿着这条射线的渲染值自然也遵循高斯分布：

where the ${\alpha }_{i}s$ are the same as in Eq.(4), and $\overline{C}(r)$,${\overline{\beta }}^2(r)$ denote the mean and variance of the rendered color through the sampled ray $r$.

其中，${\alpha }_{i}s$ 与公式(4)相同，$overlineC(r)$,KaTeX parse error: Expected 'EOF', got '}' at position 12: overline{β}}̲^2(r) 表示通过采样光线 $r$ 渲染的颜色的均值和方差。

To optimize our radiance field, we first assume that each location in the scene is at most sampled once in a training batch. We believe the hypothesis is reasonable as the intersection of two rays rarely happens in a 3D scene, let alone sampling at the same position in the same batch. Therefore, the distributions of rendered rays are assumed to be independent. In this way, we can optimize the model by minimizing the negative log-likelihood of rays $r_{i=1}^N$ from a batch $B$:

为了优化辐射场，我们首先假设场景中的每个位置在训练批次中最多采样一次。我们认为这一假设是合理的，因为在三维场景中，两条光线的交点很少发生，更不用说在同一批次的同一位置采样了。因此，我们假设渲染光线的分布是独立的。这样，我们就可以通过最小化批次 $B$ 中射线 $r_{i=1}^N$ 的负对数似然来优化模型：

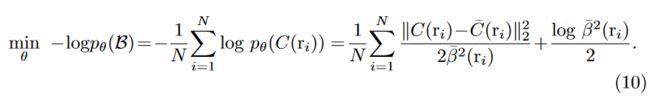
图 3. 正则化项的定性消融。正则化项会带来更明显的合成结果，并大大减轻物体表面的模糊。从数值上来说，正则化使该场景的PSNR提高了 1.1

However, simply minimizing the above objective function leads to a suboptimal solution where the weights ${\alpha }_i$ for different samples in a ray are driven closer. This results in an unexpectedly large fraction of non-zero density in the whole scene, causing blurs on the object’s surface, as depicted in Figure 3. Therefore, we add an additional regularization term to force sparser volume density, and the loss function is formulated as:

然而，简单地最小化上述目标函数会导致次优解决方案，其中光线中不同样本的权重 ${\alpha }_i$ 变得更接近。这会导致整个场景中出现大量非零密度，导致物体表面模糊，如图 3 所示。因此，我们添加一个额外的正则化项来强制稀疏体积密度，并用公式表示损失函数作为：

where λ is a hyper-parameter that controls the regularization strength.

其中 λ 是控制正则化强度的超参数。

We follow the original NeRF framework and optimize two parallel networks. To ease the difficulty of optimization, we only adopt the uncertainty branch in the fine model and keep the coarse model the same as vanilla. The final loss function is then:

我们遵循原来的 NeRF 框架，优化了两个并行网络。为了减轻优化的难度，我们仅在精细模型中采用不确定性分支，并保持粗略模型与普通模型相同。最终的损失函数为：

By learning a neural radiance field as Gaussian distributions, we not only produce reasonable predictions in uncertain areas but also present an interpretation of how NeRF model understands the scene. On the one hand, uncertainty can be viewed as a perception of noises, which may also reflect the degree of risk in real-world scenarios, e.g., robotic navigation. On the other hand, this can further serve as a vital criterion in the following active learning framework.

通过将神经辐射场学习为高斯分布，我们不仅可以在不确定区域中产生合理的预测，还可以解释 NeRF 模型如何理解场景。一方面，不确定性可以被视为对噪声的感知，这也可能反映了现实场景中的风险程度，例如机器人导航。另一方面，这可以进一步作为后续主动学习框架的重要标准。

5 ActiveNeRF

Although several works have attempted to model well-generalized NeRF under a limited training budget, the upper bound of their performances is highly restricted due to the inherent blind spot in the observations. For example, when modeling a car, if the right side of the car is never observed during training, the radiance field in this region would be under-optimized, making it almost impossible to render photo-realistic images.

尽管有几项工作尝试在有限的视角训练预算下对通用的 NeRF 进行建模，但由于观察中固有的盲点，它们的性能上限受到很大限制。例如，在对汽车进行建模时，如果在训练期间从未观察到汽车的右侧，则该区域的辐射场将优化不足，从而几乎不可能渲染逼真的图像。

Different from previous works, we target improving the upper bound of model performances. Inspired by the insights from active learning, we present a novel learning framework named ActiveNeRF and try to supplement the training sample in the most efficient manner, as illustrated in Figure 4. We first introduce how to evaluate the effect of new inputs based on the uncertainty estimation and show two approaches for the framework to incorporate with new inputs.

与之前的工作不同，我们的目标是提高模型性能的上限。受到主动学习的启发，我们提出了一种名为 ActiveNeRF 的新型学习框架，并尝试以最有效的方式补充训练样本，如图 4 所示。我们首先介绍了如何根据不确定性估计来评估新输入的影响，并展示了该框架纳入新输入的两种方法。

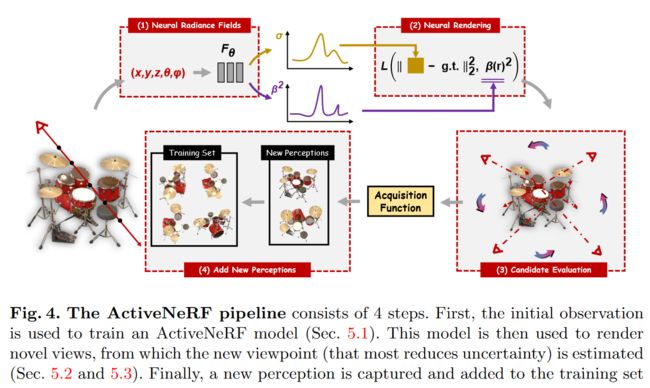
图 4.ActiveNeRF 流程由 4 个步骤组成。首先，初始观察用于训练 ActiveNeRF 模型（第 5.1 节）。然后，该模型用于渲染新颖的视图，从中估计新的视角（最大程度地减少不确定性）（第 5.2 节和第 5.3 节）。最后，捕获新的视角并将其添加到训练集中

5.1 Prior and Posterior Distribution

Estimating the influence of new data without its actual observation is a nontrivial problem. Nevertheless, modeling the radiance field as Gaussian distribution makes the evaluation more tractable, where we can estimate the posterior distribution of the radiance field based on the Bayesian rule.

在没有实际观测的情况下，估算新数据的影响不是一个简单的问题。不过，将辐射场建模为高斯分布会使评估变得更加容易，我们可以根据贝叶斯规则估计辐射场的后验分布。

Let $D_1$ denote the existing training set and $F_{\theta }$ denote the trained NeRF model given $D_1$ . For simplicity, we first consider the influence of a single ray $r_2$ from the new input $D_2$ . Thus, for the $k_{th}$ sampled location $r_2(t_k)$, its prior distribution is formulated as:

让 $D_1$ 表示现有的训练集，$F_{\theta }$ 表示给定 $D_1$ 的经过训练的 NeRF 模型。为简单起见，我们首先考虑来自新输入 $D_2$ 的单条射线 $r_2$ 的影响。因此，对于 $k_{th}$ 取样位置 $r_2(t_k)$，其先验分布可表述为

Following the sequential Bayesian formulation, the posterior distribution can then be derived as:

按照顺序贝叶斯公式，后验分布可以导出为：

As derived in Sec. 4, rendered color of rays follows the Gaussian distribution:

正如在第 4 节中得出的，渲染的光线颜色服从高斯分布：

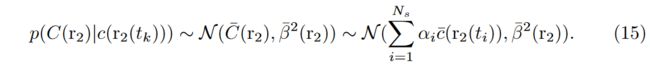
As other sampled locations in $r_2$ are independent with $r_2(t_k)$, we can represent the unrelated part in the mean as a constant $b(t_k)$ and the distribution can be simplified as:

由于 $r_2$ 中的其他采样位置与 $r_2(t_k)$ 无关，我们可以将均值中不相关的部分表示为常数 $b(t_k)$，并且分布可以简化为：

Finally, by substituting terms in Eq.(38) with Eq.(31) and Eq.(25), the posterior distribution is formulated as:

最后，将式（38）中的项替换为式（31）和式（25），后验分布可表示为：

Please refer to Appendix A for details.

详情请参阅附录A。

5.2 Acquisition Function

With the posterior distribution formulated by the Bayesian rule, we quantitatively analyze the influence on the radiance field given a new input ray. As shown in Eq.(34), although the mean of the posterior distribution is unavailable due to the unknown of $C(r_2)$, the variance is independent of the ground truth value and therefore can be precisely computed based on the current model $F_{\theta }$. Additionally, it is worth noting that the variance of the posterior distribution of a newly observed location $r_2(t_k)$ is consistently smaller than its prior distribution:

利用贝叶斯法则计算出的后验分布，我们可以定量分析新输入光线对辐射场的影响。如公式(34)所示，虽然由于未知 $C(r_2)$，无法获得后验分布的均值，但方差与地面实况值无关，因此可以根据当前模型 $F_{\theta }$ 精确计算。此外，值得注意的是，新观测到的位置 $r_2(t_k)$ 的后验分布方差始终小于其先验分布：

This further proves that new observations can genuinely reduce the uncertainty of the radiance field. On this basis, we consider the reduction of variance as the estimation of information gain of $r_2(t_k)$ from the new ray $r_2$:

这进一步证明，新的观测数据可以真正减少辐射场的不确定性。在此基础上，我们将方差的减小视为从新射线 $r_2$ 估算 $r_2(t_k)$ 的信息增益：

For a given image with resolution $H,W$ , we can sample $N=H\times W$ independent rays, with $N_s$ sampled locations from each ray. Therefore, we add up the reduction of variance from all these locations and define the acquisition function as:

对于分辨率为 $H、W$ 的给定图像，我们可以对 $N=H\times W$ 的独立射线进行采样，每条射线的采样位置为 $N_s$。因此，我们将所有这些位置的方差减少量相加，并将获取函数定义为:

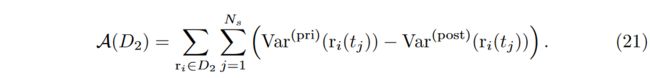
Similar derivation is also applicable with multiple input images, where the variance of posterior uncertainty is formulated as:

类似的推导也适用于多个输入图像，其中后验不确定性的方差被公式化为：

where $r_i$ denotes ray from different images, and $x=r_i(t_{k_i}),\forall i$. Please refer to Appendix B for details.。
In practical implementation, we first sample candidate views from a spherical space, and choose the top-k candidates that score highest in the acquisition function as the supplementary of the current training set. In this way, the captured new inputs bring the most information gain and promote the performance of the current model with the highest efficiency.
Besides, a quality-efficiency trade-off can also be achieved by evaluating new inputs with lower resolution. For example, instead of using full image size $H\times W$ as new rays, we can sample $H/r\times W/r$ rays to approximate the influence of the whole image with only $1/r^2$ time consumption.

其中，$r_i$ 表示来自不同图像的射线，$x=r_i(t_{k_i}),\forall i$。详情请参阅附录 B。
在实际应用中，我们首先从一个球形空间中抽取候选视图，然后选择在获取函数中得分最高的前 k 个候选视图作为当前训练集的补充。这样，捕捉到的新输入会带来最大的信息增益，并以最高的效率提升当前模型的性能。
此外，还可以通过评估分辨率较低的新输入来实现质量和效率的权衡。例如，我们可以不使用整个图像大小 $H\times W$ 作为新射线，而是对 $H/r\times W/r$ 的射线进行采样，以近似整个图像的影响，耗时仅为 $1/r^2$。

5.3 Optimization and Inference

With the newly captured samples chosen by the acquisition function, we provide two approaches to incorporate the current NeRF model with additional inputs.
Bayesian Estimation.
With the ground-truth value $C(r)$ from the new inputs, we can practically compute the posterior distribution of the locations in the scene by leveraging Eq.(34). Among these, the mean of distribution becomes the Bayesian estimation of emitted radiance value, and can be adopted in the rendering process. At inference time, we only need to substitute the prior color with the posterior Bayesian estimation:

通过采集函数选择新捕获的样本，我们提供了两种方法将当前的 NeRF 模型与附加输入相结合。
贝叶斯估计。
利用新输入的真实值 $C(r)$ ，我们实际上可以利用方程（34）计算场景中位置的后验分布。其中，分布均值成为发射辐射值的贝叶斯估计，可以在渲染过程中采用。在推理时，我们只需要用后验贝叶斯估计替换先验颜色：

while others remain unchanged. One of the advantages of using Bayesian estimation is that we avoid the collateral training procedure. If we consider an edge device, e.g., a robot, the training-free scheme allows the agent to perform offline inference instantly, which is more friendly in resource-constrained scenarios.
Continuous Learning can also be considered if time and computation resources are not the bottlenecks. The captured inputs can be added to the training set and tune the model on the basis of the current one. We can further control the fraction of training rays from new images, forcing the model to optimize in the newly observed regions. The two approaches can both promote the quality of the neural radiance field, and naturally achieve a trade-off between efficiency and synthesis quality.

而其他则保持不变。使用贝叶斯估计的优点之一是我们避免了附带的训练过程。如果我们考虑终端设备，例如机器人，免训练方案允许客户端立即执行离线推理，这在资源受限的场景中更加友好。
如果时间和计算资源不是瓶颈，也可以考虑持续学习。捕获的输入可以添加到训练集中，并在当前输入的基础上调整模型。我们可以进一步控制来自新图像的训练射线的比例，迫使模型在新观察到的区域进行优化。
这两种方法都可以提升神经辐射场的质量，自然地实现效率和合成质量之间的权衡。

表 1. 固定训练集设置中的定量结果：ActiveNeRF 在所有设置中均优于或与原始 NeRF 相当。特别要注意的是，我们的模型在低样本设置中的表现明显优于 NeRF。我们报告 PSNR/SSIM（越高越好）和 LPIPS（越低越好）

6 Experiments

6.1 Experimental setup

Datasets.
We extensively demonstrate our approach in two benchmarks, including LLFF [19] and NeRF [20] datasets. LLFF is a real-world dataset consisting of 8 complex scenes captured with a cellphone. Each scene contains 20-62 images with 1008 × 756 resolution, where 1/8 images are reserved for the test. NeRF dataset contains 8 synthetic objects with complicated geometry and realistic non-Lambertian materials. Each scene has 100 views for training and 200 for the test, and all the images are at 800 × 800 resolution. See detailed training configurations in the Appendix.
Metrics.
We report the image quality metrics PSNR and SSIM for evaluations. We also include LPIPS [38], which more accurately reflects human perception.

数据集。
我们在两个基准测试中广泛展示了我们的方法，包括 LLFF [19] 和 NeRF [20] 数据集。 LLFF 是一个真实世界的数据集，由手机捕获的 8 个复杂场景组成。每个场景包含20-62张分辨率为1008×756的图像，其中1/8图像保留用于测试。 NeRF 数据集包含 8 个具有复杂几何形状和真实非朗伯材料的合成对象。每个场景有 100 个视图用于训练，200 个视图用于测试，所有图像的分辨率均为 800 × 800。请参阅附录中的详细训练配置。
指标。
我们报告图像质量指标 PSNR 和 SSIM 以进行评估。我们还包括 LPIPS [38]，它更准确地反映了人类的感知。

图 5. 使用不同比例的训练样本的合成场景和真实场景的定性结果。可以进行几个观察：首先，ActiveNeRF 在低样本设置中的表现明显优于 NeRF（例如，参见 Ln. 2 和 3）。其次，当使用更多数据时，不确定性会正确减少（参见上栏不确定性图）。最后，当使用所有图像时，ActiveNeRF 和 NeRF 获得相似的定性性能（参见 Ln. 1 和 4），这表明建模不确定性对视图合成的质量没有负面影响

6.2 Results

Uncertainty Estimation.
We first evaluate the effectiveness of the proposed uncertainty estimation with different fractions of input samples. We compare with several competitive baselines, including Neural Radiance Fields (NeRF) [35], Local Light Field Fusion (LLFF) [19], and Scene Representation Networks (SRN) [30]. We also compare with three competitive baselines, including IBRNet [34], MSVNeRF [5] and DietNeRF [10].

不确定性估计。
我们首先使用不同比例的输入样本评估所提出的不确定性估计的有效性。我们与几个竞争基线进行比较，包括神经辐射场（NeRF）[35]、局部光场融合（LLFF）[19]和场景表示网络（SRN）[30]。我们还与三个竞争基线进行比较，包括 IBRNet [34]、MSVNeRF [5] 和 DietNeRF [10]。

We show the performance of our proposed approach with a different number of training data over baseline approaches in Table 7. It can be seen that NeRF with uncertainty performs on par or slightly better than baseline models, showing that modeling uncertainty does not affect the quality of synthesizing novel views. When it comes to limited training samples, our model shows consistently better results. For example, in the synthetic dataset, NeRF with 10% training data fails to generalize well to some views, while our model can still provide reasonable predictions. The gap is more distinct on the perceptual loss, e.g., LPIPS, showing that our model can also render high-frequency textures with limited training data. Compared to DietNeRF, our model achieves better performances on two criteria and is competitive on the third. However, ours do not require additional pretrained model (e.g., CLIP for DietNeRF) and can be used in the following active learning framework. Qualitative results are shown in Figure 5.

我们在表 7 中展示了我们提出的方法在不同数量的训练数据下相对于基线方法的性能。可以看出，具有不确定性的 NeRF 与基线模型表现相当或略好，这表明建模不确定性不会影响合成新视角的质量。当涉及有限的训练样本时，我们的模型始终显示出更好的结果。例如，在 synthetic 数据集中，具有 10% 训练数据的 NeRF 无法很好地泛化到某些视图，而我们的模型仍然可以提供合理的预测。在感知损失（例如 LPIPS）上，差距更加明显，这表明我们的模型还可以使用有限的训练数据渲染高频纹理。与 DietNeRF 相比，我们的模型在两个标准上实现了更好的性能，并且在第三个标准上具有竞争力。然而，我们的模型不需要额外的预训练模型（例如 DietNeRF 的 CLIP），并且可以在以下主动学习框架中使用。定性结果如图 5 所示。

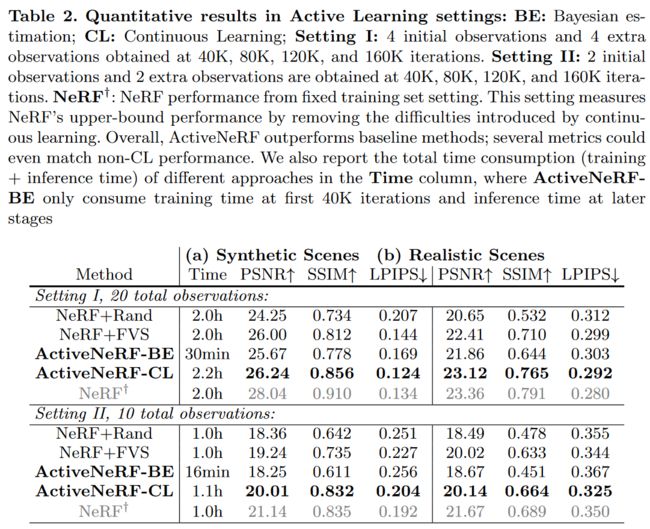
表 2. 主动学习设置中的定量结果：BE：贝叶斯估计； CL：持续学习；设置 I：4 个初始观测值和 40K、80K、120K 和 160K 次迭代获得的 4 个额外观测值。设置 II：在 40K、80K、120K 和 160K 迭代时获得 2 个初始观测值和 2 个额外观测值。 NeRF†：固定训练集设置的 NeRF 性能。此设置通过消除持续学习带来的困难来衡量 NeRF 的上限性能。总体而言，ActiveNeRF 优于基线方法；有几个指标甚至可以与非 CL 性能相匹配。我们还在 Time 列中报告了不同方法的总时间消耗（训练 + 推理时间），其中 ActiveNeRFBE 仅消耗前 40K 迭代的训练时间和后期阶段的推理时间

ActiveNeRF. We validate the performance of our proposed framework, ActiveNeRF, and compare it with two heuristic approaches. As an approximation, we hold out a large fraction of images in the training set and use these images as candidate samples. For baselines, we denote NeRF+Random as randomly capturing new images in the candidates. NeRF+FVS (furthest view sampling) corresponds to finding the candidates with the most distanced camera position compared with the current training set. We empirically adjust the number of the initial training set and captured samples during the training procedure.

ActiveNeRF。
我们验证了我们提出的框架 ActiveNeRF 的性能，并将其与两种启发式方法进行比较。作为近似，我们在训练集中保留大部分图像，并将这些图像用作候选样本。对于基线，我们将 NeRF+Random 表示为随机捕获候选图像中的新图像。 NeRF+FVS（最远视图采样）对应于寻找与当前训练集相比相机位置最远的候选者。我们根据经验调整初始训练集和训练过程中捕获样本的数量。

We first show the results with continuous learning scheme, where the time and computation resources are considered sufficient. The comparison results are shown in Table 4 and Figure 6. We can easily see that ActiveNeRF captures the most informative inputs comparing with heuristic approaches, which contributes most to synthesizing views from less observed regions. The additional training cost for ActiveNeRF is also comparably minor (2.2h vs. 2h).

我们首先展示连续学习方案的结果，其中时间和计算资源被认为是足够的。比较结果如表 4 和图 6 所示。我们可以很容易地看到，与启发式方法相比，ActiveNeRF 捕获了最具信息量的输入，这对合成观察较少区域的视图贡献最大。 ActiveNeRF 的额外训练成本也相对较小（2.2 小时与 2 小时）。

We further validate the model performances with Bayesian estimation. As shown in Table 4, 75% of the time consumption can be saved. Although showing inferior performance to continuous learning, the model with Bayesian estimation still synthesize reasonable images and is even competitive with heuristic approaches under continuous learning scheme.

我们通过贝叶斯估计进一步验证模型性能。如表4所示，可以节省75%的时间消耗。尽管表现不如连续学习，但采用贝叶斯估计的模型仍然可以合成合理的图像，甚至可以与连续学习方案下的启发式方法相媲美。

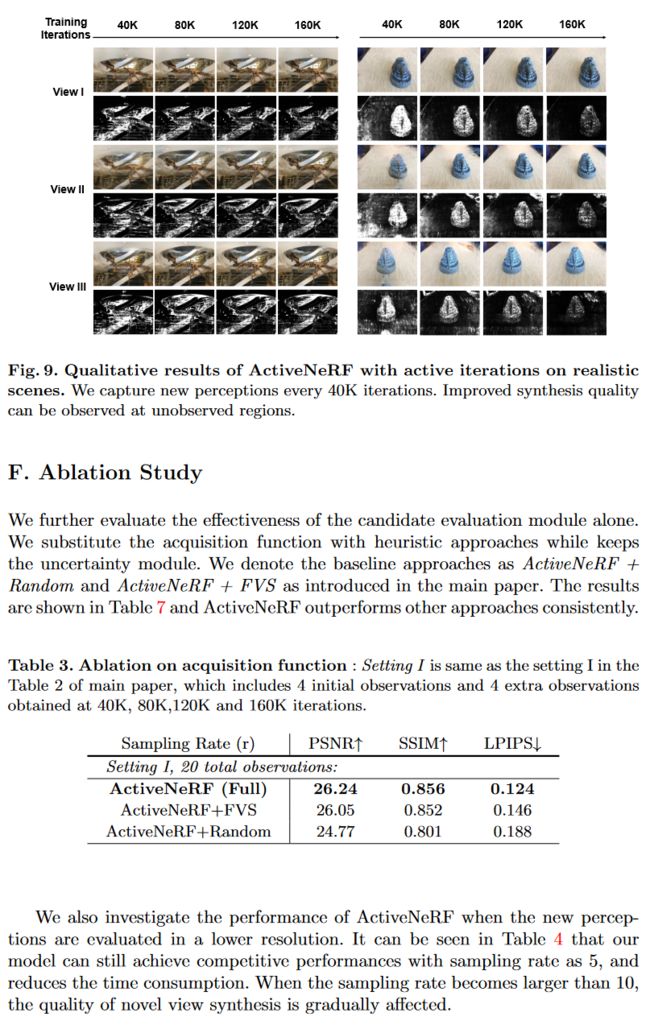
图 6. ActiveNeRF 经过四次主动迭代的定性结果。每 40K 次迭代我们都会纳入新的输入。在未观察到的区域可以看到合成质量的提高

7 Conclusion

In this paper, we present a flexible learning framework, that supplements the existing training set with newly captured samples based on an active learning scheme. We first incorporate uncertainty estimation into a NeRF model and evaluate the reduction of uncertainty in the scene given new inputs. By selecting the samples that bring the most information gain, the quality of novel view synthesis can be promoted with minimal additional resources. Also, our approach can be applied to various NeRF-extension approaches as a plug-in module, and enhance model performances in a resource-efficient manner.

在本文中，我们提出了一种灵活的学习框架，它基于主动学习方案用新捕获的样本补充了现有的训练集。我们首先将不确定性估计纳入 NeRF 模型中，并评估给定新输入的场景中不确定性的减少情况。通过选择带来最多信息增益的样本，可以用最少的额外资源来提高新颖视图合成的质量。此外，我们的方法可以作为插件模块应用于各种 NeRF 扩展方法，并以资源高效的方式增强模型性能。

附录：

---

抛砖：

1. 也是用的bayes框架来进行不确定性评估。
2. 它虽然需要参与训练过程中，但是他通过不确定性的评估来确定来有优先级地纳入新的输入，可以避免输入视角相似的数据，高效迭代得到最终结果结果。
3. 针对特定场景，在数据或者效率上的优化，在新视角合成质量上没有明显改善。
4. 看上去，输入的即使是稀疏视角，也需要均匀分布。