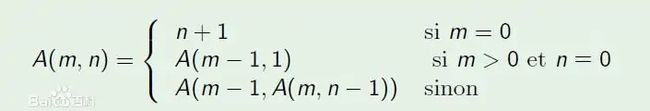编程题实训-栈
超详解版
第1关:基于栈的中缀算术表达式求值
任务描述
本关任务:输入一个中缀算术表达式,求解表达式的值。运算符包括+、-、*、/、(、)、=,参加运算的数为double类型且为正数。(要求:直接针对中缀算术表达式进行计算,不能转换为后缀或前缀表达式再进行计算,只考虑二元运算即可。)
编程要求
输入
多组数据,每组数据一行,对应一个算术表达式,每个表达式均以“=”结尾。当表达式只有一个“=”时,输入结束。参加运算的数为double类型。
输出
对于每组数据输出一行,为表达式的运算结果。输出保留两位小数。
#include
#include
#define MAXSIZE 100
#define OK 1
#define ERROR 0
#define OVERFLOW -2
using namespace std;
typedef struct
{//运算符栈
char *base;
char *top;
int stacksize;
}SqStack1;
int InitStack1(SqStack1 &S)
{//运算符栈初始化
S.base=new char[MAXSIZE]; //1.分配内存空间 2.指向空间
if(!S.base) return OVERFLOW; //如果S.base为 NULL或0,则返回溢出的值。
S.top=S.base;
S.stacksize=MAXSIZE;
return OK;
}
int Push1(SqStack1 &S, char e)
{//运算符栈入栈
if(S.top-S.base==S.stacksize) //栈满
return ERROR;
*S.top=e;
S.top++;
return OK;
}
int Pop1(SqStack1 &S)
{//运算符栈出栈
if(S.top==S.base) //栈空
return ERROR;
S.top--;
return OK;
}
char GetTop1(SqStack1 S)
{//运算符栈取栈顶元素
if(S.top!=S.base)
return *(S.top-1);
return ERROR;
}
typedef struct
{//操作数栈
double *base;
double *top;
int stacksize;
}SqStack2;
int InitStack2(SqStack2 &S)
{//操作数栈初始化
S.base=new double[MAXSIZE];
if(!S.base) return OVERFLOW;
S.top=S.base;
S.stacksize=MAXSIZE;
return OK;
}
int Push2(SqStack2 &S,double e)
{//操作数栈入栈
if(S.top-S.base==S.stacksize) //栈满
return ERROR;
*S.top=e;
S.top++;
return OK;
}
int Pop2(SqStack2 &S)
{//操作数栈出栈
if(S.top==S.base) //栈空
return ERROR;
S.top--;
return OK;
}
double GetTop2(SqStack2 S)
{//操作数栈取栈顶元素
if(S.top!=S.base)
return *(S.top-1);
return ERROR;
}
double Calculate(double a,char op,double b)
{//计算表达式“a op b”的值
switch(op)
{
case '+':return a+b;
case '-':return a-b;
case '*':return a*b;
case '/':return a/b;
}
}
char Precede(char a,char b)
{//比较运算符a和b的优先级
if((a=='('&&b==')')||(a=='='&&b=='='))
return '=';
else if(a=='('||a=='='||b=='('||(a=='+'||a=='-')&&(b=='*'||b=='/'))
return '<';
else
return '>';
}
double EvaluateExpression(SqStack1 OPTR,SqStack2 OPND,char s[])
{//算术表达式求值的算符优先算法
/**************begin************/
int i,x=0,e=0,flag=0;
for(i=0;s[i]!='\0';i++){
if('0'<=s[i]&&s[i]<='9'){
flag = 1;//判断double类型是否处理完,1未完成
x=x*10+(s[i]-'0');
if(e!=0) e=e*10;
}else if(s[i]=='.'){
e = 1;
}else{
if(flag!=0){
double number = x;
if(e!=0) number = number/e;
Push2(OPND,number);
x=e=flag=0;
}
while(1){
if(Precede(GetTop1(OPTR),s[i])=='<'){
Push1(OPTR,s[i]);
break;
}else if(Precede(GetTop1(OPTR),s[i])=='>'){
double b = GetTop2(OPND);
Pop2(OPND);
double a = GetTop2(OPND);
Pop2(OPND);
char oper = GetTop1(OPTR);
Pop1(OPTR);
Push2(OPND,Calculate(a,oper,b));
}else{
Pop1(OPTR);
break;
}
}
}
}
return GetTop2(OPND);
/**************end************/
}
int main()
{//设OPTR和OPND分别为运算符栈和操作数栈
SqStack1 OPTR;
InitStack1(OPTR); //初始化OPND栈
SqStack2 OPND;
InitStack2(OPND); //初始化OPTR栈
Push1(OPTR,'='); //将表达式起始符“=”压入OPTR栈
char s[100];
while(cin>>s)
{//循环读入多组数据
if(s[0]=='=')
break; //当表达式只有一个“=”时,输入结束
//输出中缀算术表达式的值
cout< double EvaluateExpression(SqStack1 OPTR,SqStack2 OPND,char s[]) 这个函数接收三个参数:一个名为OPTR的操作符栈,一个名为OPND的操作数栈,和一个字符数组s表示待求解的算术表达式。
主要逻辑:
这个函数主要通过遍历输入的算术表达式字符串s来处理每个字符。
a. 遍历表达式的每个字符:
对于每个字符s[i],函数首先检查它是否是一个数字字符(0-9)。如果是,函数会将其转换为对应的整数值,并累加到当前的数值中。如果e不为0,说明当前的数值是一个小数,函数会相应地调整累加方式。
如果字符是一个小数点.,函数会设置一个标志e=1,表示接下来应该处理小数部分。
如果字符是一个运算符(比如+, -, *, /),函数会检查是否已经处理完了一个操作数的所有内容(由标志flag判断)。如果已经处理完了一个操作数,函数会将这个操作数存入OPND栈中,并重置相关变量。
然后,函数会使用一个循环来处理栈中优先级更高的运算符。具体来说,它会不断地从OPTR栈顶取出一个运算符,直到找到一个优先级低于当前运算符的运算符或者栈为空为止。
在这个过程中,函数会根据运算符的优先级从高到低进行相应的计算,并将结果存入OPND栈中。例如,如果当前运算符是乘法*,函数会取出栈顶的两个操作数,进行乘法运算,并将结果存入栈中。
b. 处理完一个运算符后:
如果遍历完整个表达式后,还有剩余的运算符没有处理,函数会继续从OPTR栈顶取出剩余的运算符并处理它们。
c. 返回结果:
最后,函数会返回栈顶的操作数作为整个表达式的计算结果。
第2关:双栈的基本操作
双栈共享一个地址连续的存储单元。即程序同时需要两个栈时,可以定义一个足够大的栈空间,该空间的两端分别设为两个栈的栈底
双栈结构的主要优点有:
- 可以有效利用栈空间,不需要移动大量元素,插入和删除元素时只需要移动栈顶指针,时间复杂度为O(1)。
- 可以同时处理两个栈,两个栈的添加和删除元素操作相互独立,因此可以实现多个栈共享同一个栈空间,提高空间利用率。
然而,双栈结构也存在一些缺点:
- 两个栈是此消彼长的关系,导致两个栈分别的栈长是动态变化的,无法确定。
- 双栈结构在实际运算过程中,一个栈有可能进栈元素多而体积大些,另一个则可能小些。因此,如果运算较为复杂或者长度为定值,可能会产生时间代价较高的问题。
在实际使用中,双栈结构适用于以下情况:
- 需要同时使用多个栈,并且每个栈的元素数量不确定,可能存在一个栈元素多而另一个栈元素少的情况。
- 需要尽可能减少元素的移动量,以加快处理速度。例如,在表达式求值等操作中,使用双栈结构可以减少元素的移动量,提高处理效率。
- 需要尽可能减少空间浪费。例如,如果给几个栈分配同样大小的空间,可能实际运行时,有的栈膨胀得快,很快就产生了溢出,而其他的栈可能此时还有许多空闲空间。使用双栈结构可以避免这种情况的发生。
任务描述
本关任务:将编号为0和1的两个栈存放于一个数组空间V[m]中,栈底分别处于数组的两端。当第0号栈的栈顶指针top[0]等于-1时该栈为空;当第1号栈的栈顶指针top[1]等于m时,该栈为空。两个栈均从两端向中间增长(见下图)。试编写双栈初始化,判断栈空、栈满、进栈和出栈算法的函数。函数调用次序依次为:进栈、栈满的判断、出栈、栈空的判断。
双栈数据结构的定义如下:
typedef struct
{
int top[2], bot[2]; //栈顶和栈底指针
SElemType *V; //栈数组
int m; //栈最大可容纳元素个数
}DblStack;
编程要求
输入
多组数据,每组数据有四行,每行的数据之间均用空格分隔。第一行为一个整数m,表示数组V的大小,第二行为四个整数e0、e1、d0、d1,e0和e1分别代表压入0号栈和1号栈的整数序列E0和E1的长度(依次连续入栈,中间没有出栈的情况),d0和d1分别代表从0号栈和1号栈弹出的序列的长度(依次连续出栈,中间没有入栈的情况)。第三行和第四行分别表示序列E0和E1。当m=0时,输入结束。
输出
对于每组数据输出三行。第一行代表进栈操作完成时栈是否为满(出栈操作尚未执行),栈满输出1,栈不满输出0。第二行和第三行的数据分别对应0号栈和1号栈。第二行包括d0+1个整数,其中前d0个整数代表出栈序列D0,最后一个整数代表出栈操作完成时0号栈是否为空,栈空输出0,不空输出1。第三行包括d1+1个整数,其中前d1个整数代表出栈序列D1,最后一个整数代表出栈操作完成时1号栈是否为空,栈空输出0,不空输出1。整数之间用空格分隔。
#include
using namespace std;
typedef struct
{
int top[2],bot[2];//栈顶和栈底指针
int *V;//栈数组
int m;//栈最大可容纳元素个数
}DblStack;
void InitDblStack(DblStack &S,int m)
{//初始化一个大小为m的双向栈
S.V=new int[m]; //动态分配一个最大容量为m的数组空间
S.bot[0]=-1; //左栈栈底指针
S.bot[1]=m; //右栈栈底指针
S.top[0]=-1; //左栈栈顶指针
S.top[1]=m; //右栈栈顶指针
}
int IsEmpty(DblStack S,int i)
{//判断指定的i号栈是否为空,空返回1,否则返回0
return S.top[i]==S.bot[i];
}
int IsFull(DblStack S)
{//判断栈是否满,满则返回1,否则返回0
if(S.top[0]+1==S.top[1]) return 1;
else return 0;
}
void Push(DblStack &S,int i)
{//向指定的i号栈中插入元素x,先移动指针再入栈
/**************begin************/
//插入元素,得考虑是否栈满
if(S.top[0]+1 == S.top[1]) return;
int x;
cin>>x;
if(i==0) S.top[i]++;
else S.top[i]--;
S.V[S.top[i]] = x;
/**************end************/
}
void Pop(DblStack &S,int i)
{//删除指定的i号栈的栈顶元素,先出栈再移动指针
/**************begin************/
if(S.top[i] == S.bot[i]) return; //栈空
cout<>m)
{
if(m==0) break;
InitDblStack(S,m);
cin>>e0>>e1>>d0>>d1;
while(e0--)
Push(S,0);
while(e1--)
Push(S,1);
cout< 画个图就能很好的理清关系了,提示,在栈顶插入元素
第3关:基于栈的回文字符序列判断
任务描述
本关任务:回文序列是正反读均相同的字符序列,如“abba”和“abdba”均是回文,但是“good”不是回文。请设计一个算法判定给定的字符序列是否为回文。
编程要求
输入
多组数据,每组数据有一行。每一行为一个长度不定的字符序列A。当A为“0”时,输入结束。
输出
对于每组数据输出一行。若字符序列A是回文序列,则输出“YES”,否则输出“NO”。
#include
#define MAXSIZE 100
#define OK 1
#define ERROR 0
#define OVERFLOW -2
using namespace std;
typedef struct
{
char *base;
char *top;
int stacksize;
}SqStack;
int InitStack(SqStack &S)
{//栈初始化
S.base=new char[MAXSIZE];
if(!S.base) return OVERFLOW;
S.top=S.base;
S.stacksize=MAXSIZE;
return OK;
}
int Push(SqStack &S, char e)
{//入栈
if(S.top-S.base==S.stacksize) //栈满
return ERROR;
*S.top=e;
S.top++;
return OK;
}
int Pop(SqStack &S)
{//出栈返回栈顶元素
if(S.top==S.base) //栈空
return ERROR;
S.top--;
return *S.top;
}
int IsPalindrome(SqStack &S,char *t)
{//判断栈的回文字符序列
/**************begin************/
//1.入栈 2.按正常判断回文的思路走
//出栈入栈的代码要烂熟于心
int len = 0;
for (int i = 0; t[i] != '\0'; i++) { // 先将输入字符串的所有字符压入栈中
Push(S, t[i]);
len++;
}
for(int i = 0;i < len/2;i++){
if(t[i] != Pop(S)) return 0;
}
return 1;
/**************end************/
}
int main()
{
char t[100];
while(cin>>t&&t[0]!='0')
{
SqStack S;
InitStack(S);
if(IsPalindrome(S,t)==1) cout<<"YES"< 这段代码的目的是输入一个字符串,然后判断它是否是回文。每次输入一个字符串,就会进行一次这样的判断。如果输入的字符串是回文,程序会输出"YES",否则输出"NO"。这个过程会一直循环进行,直到遇到空字符串或者用户按下结束输入的快捷键。
第4关:入栈和出栈的基本操作
任务描述
本关任务:输入一个整数序列a1,a2,a3...,an。当ai不等于-1时将ai进栈;当ai=-1时,输出栈顶元素并将其出栈。
编程要求
输入
多组数据,每组数据有两行,第一行为序列的长度n,第二行为n个整数,整数之间用空格分隔。当n=0时输入结束。
输出
对于每一组数据输出若干行。每行为相应的出栈元素。当出栈异常时,输出“POP ERROR”并结束本组数据的输出。
#include
using namespace std;
#define MAXSIZE 100
#define OK 1
#define ERROR 0
#define OVERFLOW -2
typedef struct
{
int *base;
int *top;
int stacksize;
}SqStack;
int InitSqStack(SqStack &S)
{//栈的初始化
S.base=new int[MAXSIZE];
if(!S.base) return OVERFLOW;
S.top=S.base;
S.stacksize=MAXSIZE;
return OK;
}
int Push(SqStack &S,int e)
{//入栈
if(S.top-S.base==S.stacksize) //栈满
return ERROR;
*S.top=e;
S.top++;
return OK;
}
int Pop(SqStack &S)
{//出栈
if(S.top==S.base) //栈空
return ERROR;
S.top--;
return OK;
}
int GetTop(SqStack S)
{//取栈顶元素
if(S.top==S.base) //栈空
return ERROR;
return *(S.top-1);
}
void InOutS(SqStack &S,int a[],int n)
{//入栈和出栈的基本操作
/**************begin************/
for(int i = 0;i < n;i++){
if(a[i]!=-1) Push(S,a[i]);
else{
if(S.top!=S.base){
cout<>n)
{
if(n==0) break;
SqStack S;
InitSqStack(S);
int a[n];
for(int i=0;i>a[i]; //整数序列
InOutS(S,a,n);
}
return 0;
} 第5关:基于栈的后缀算术表达式求值
后缀算术表达式(逆波兰表示法)和中缀算术表达式(常规表示法)是两种不同的算术表达式表示方法。它们的主要区别在于运算符的放置位置和计算顺序。
基于栈的实现方式,对于这两种表示法的求值过程也有所不同:
- 中缀算术表达式(Infix Expression):
在中缀表达式中,运算符位于两个操作数之间。因此,在计算时需要先从左到右扫描表达式,将操作数入栈,然后根据运算符进行计算。例如,对于表达式 "2 + 3",首先将数字2和3入栈,然后根据"+"运算符进行计算,得到结果5。
在中缀表达式求值过程中,需要遵循从左到右的顺序进行计算,因此扫描表达式的顺序是关键。
- 后缀算术表达式(Postfix Expression):
在后缀表达式中,运算符位于两个操作数之后。因此,在计算时需要先从左到右扫描表达式,将操作数入栈,然后根据栈顶元素进行计算。例如,对于表达式 "2 3 +",首先将数字2和3入栈,然后根据栈顶的"+"运算符进行计算,得到结果5。
在后缀表达式求值过程中,需要遵循从右到左的顺序进行计算,因此栈的运用和操作顺序是关键。
总结:
基于栈的后缀算术表达式求值和中缀算术表达式求值的主要区别在于:
- 中缀表达式中,运算符位于两个操作数之间;而后缀表达式中,运算符位于两个操作数之后。
- 在求值过程中,中缀表达式需要从左到右扫描并计算,而后缀表达式需要从右到左扫描并计算。
- 中缀表达式需要遵循从左到右的计算顺序,而后缀表达式需要遵循从右到左的计算顺序。
任务描述
本关任务:从键盘上输入一个后缀表达式,试编写算法计算表达式的值。规定:后缀表达式的长度不超过一行,以“=”作为输入结束,操作数之间用空格分隔,操作符只可能有+、?、*、/四种运算。
编程要求
输入
多组数据,每组数据一行,对应一个后缀算术表达式,每个表达式均以“=”结尾。当表达式只有一个“=”时,输入结束。
输出
运行分析 例如"1 2 + 8 2 - 7 4 - / * ="。
对于每组数据输出一行,为表达式的运算结果。
-
初始化一个空的栈OPND。
-
开始遍历输入字符串s:
-
1:这是一个数字,所以将其推入栈中:OPND = [1]
-
2:将其推入栈中:OPND = [1, 2]
-
+:这是一个运算符,因此从栈中弹出顶部的两个数字,执行加法,并将结果推回栈中:OPND = [3]
-
8:将其推入栈中:OPND = [3, 8]
-
2:将其推入栈中:OPND = [3, 8, 2]
-
-:这是一个运算符,因此从栈中弹出顶部的两个数字,执行减法,并将结果推回栈中:OPND = [3, 6]
-
7:将其推入栈中:OPND = [3, 6, 7]
-
4:将其推入栈中:OPND = [3, 6, 7, 4]
-
-:这是一个运算符,因此从栈中弹出顶部的两个数字,执行减法,并将结果推回栈中:OPND = [3, 6, 3]
-
/:这是一个运算符,因此从栈中弹出顶部的两个数字,执行除法,并将结果推回栈中:OPND = [3, 2]
-
*:这是一个运算符,因此从栈中弹出顶部的两个数字,执行乘法,并将结果推回栈中:OPND = [6]
-
=:这是表达式的结束。
#include
#include
#include
#define MAXSIZE 100
#define OK 1
#define ERROR 0
#define OVERFLOW -2
using namespace std;
typedef struct
{//数字栈
double *base;
double *top;
int stacksize;
}SqStack;
int InitStack(SqStack &S)
{//数字栈初始化
S.base=new double[MAXSIZE];
if(!S.base) return OVERFLOW;
S.top=S.base;
S.stacksize=MAXSIZE;
return OK;
}
int Push(SqStack &S,double e)
{//数字栈入栈
if(S.top-S.base==S.stacksize) //栈满
return ERROR;
*S.top=e;
S.top++;
return OK;
}
int Pop(SqStack &S)
{//数字栈出栈
if(S.top==S.base) //栈空
return ERROR;
S.top--;
return OK;
}
double GetTop(SqStack S)
{//数字栈取栈顶元素
if(S.top!=S.base)
return *(S.top-1);
return ERROR;
}
double Calculate(double a,char op,double b)
{//算术表达式的求值
switch(op)
{
case '+':return a+b;
case '-':return a-b;
case '*':return a*b;
case '/':return a/b;
}
}
double EvaluateExpression(SqStack OPND,char s[])
{//后缀算术表达式求值
/**************begin************/
//后缀算术表达式求值
int i,x=0,e=0,flag=0;
//x和e辅助存储double型数
//flag用于判断某个double类型数据是否读入完全
for(i=0;s[i]!='=';i++)
{
if('0'<=s[i]&&s[i]<='9')
{
flag=1;
x=x*10+(s[i]-'0');//x存储去掉小数点后的数据,如原数据1.23,最终得到的x为123
if(e!=0) e=e*10;//小数点后有几位,e扩大为10的几倍
}
else if(s[i]=='.')
e=1;
else
{
if(flag!=0)
{
double number=x;
if(e!=0) number=number/e;//如果其间有小数点出现,number缩小对应的倍数
Push(OPND,number);//将double类型数据入栈
x=e=flag=0;//复原x、e、flag
}
if(s[i]==' ') continue;
double b=GetTop(OPND);
Pop(OPND);
double a=GetTop(OPND);
Pop(OPND);
char oper=s[i];
Push(OPND,Calculate(a,oper,b));//将运算结果压入数字栈
}
}
return GetTop(OPND);
/**************end************/
}
int main()
{
char s[100];
//用字符数组存储表达式,每个数组元素仅存一个字符
while(1)
{
cin.getline(s,100); //输入一行含空格的后缀表达式
if(s[0]=='=')
break; //当表达式只有一个"="时,输入结束
SqStack OPND;
InitStack(OPND); //初始化数字栈
cout< 第6关:基于栈的可操作判断
任务描述
本关任务:假设I和O分别代表入栈和出栈操作。栈的始态和终态均为空。入栈和出栈的操作序列可以表示为仅由I和O组成的序列,称可操作的序列为合法序列,否则称为非法序列。请设计一个算法,判断所给的操作序列是否合法。若合法输出“true”,反之输出“false”。
编程要求
输入
多组数据,每组数据一行,对应一个后缀算术表达式,每个表达式均以“=”结尾。当表达式只有一个“=”时,输入结束。
输出
多组数据,每组数据为一行长度不定的操作序列A。当A为“0”时,输入结束。
#include
#define MAXSIZE 100
#define OK 1
#define ERROR 0
#define OVERFLOW -2
using namespace std;
typedef struct
{
char *base;
char *top;
int stacksize;
}SqStack;
int InitStack(SqStack &S)
{//初始化栈
S.base=new char[MAXSIZE];
if(!S.base) return OVERFLOW;
S.top=S.base;
S.stacksize=MAXSIZE;
return OK;
}
int Push(SqStack &S)
{//入栈
S.top++;
return OK;
}
int Pop(SqStack &S)
{//出栈
S.top--;
return OK;
}
int IsEmpty(SqStack S)
{//判断栈是否为空,空返回1,否则返回0
return S.top==S.base;
}
bool Judge(char a[],SqStack &S)
{//栈的可操作判断
/**************begin************/
int i = 0;
//写循环前先思考是否知道运行次数
while(a[i] != '\0'){ //'\0' 表示空字符(null字符)
if(a[i] == 'I'){
if(S.top - S.base == S.stacksize) return false;
Push(S);
}else if(a[i] == 'O'){
if(S.top == S.base) return false;
Pop(S);
}
i++;
}
return IsEmpty(S);
/**************end************/
}
int main()
{
char a[100];
while(cin>>a)
{
if(a[0]=='0') break;
SqStack op;
InitStack(op);
if(Judge(a,op)) cout<<"TRUE"< 答案2
bool Judge(char a[],SqStack &S)
{//栈的可操作判断
/**************begin************/
//答案2
int i = 0;
while(a[i]!='\0'){
switch(a[i]){
case 'I':{
if(S.top-S.base==S.stacksize) return false;
else Push(S);
break;
}
case 'O':{
if(S.top == S.base) return false;
else Pop(S);
break;
}
}
i++;
}
//判断栈的终态是否为空
if(IsEmpty(S)) return true;
else return false;
/**************end************/
}本关主要是审题的问题,关于栈我们主要考虑是否栈满,是否栈空。 本题要求栈的始态和终态均为空,再加个判断条件就好了。
第7关:Ackermann函数的递归求值
任务描述
本关任务: 已知Ackermann函数定义如下:
写出计算Ack(m,n)的递归算法。
编程要求
输入
多组数据,每组数据有一行,为两个整数m和n。当m和n都等于0时,输入结束。
输出
每组数据输出一行,为Ack(m,n)。
#include
using namespace std;
int Ack(int m,int n)
{//Ackermann函数的递归求值
/**************begin************/
if(m==0){
return n+1;
}else if(m > 0 && n == 0){
return Ack(m-1,1);
}else{
return Ack(m-1,Ack(m,n-1));
}
/**************end************/
}
int main()
{
int m,n;
while(cin>>m>>n)
{
if(m==0&&n==0) break;
cout< 第8关:Ackermann函数的非递归求值
#include
using namespace std;
#define MAXSIZE 100
int Ack(int m,int n)
{//Ackermann函数的非递归求值
/**************begin************/
int tmp[m + 1][MAXSIZE];
for (int j = 0; j < MAXSIZE; j ++)
tmp[0][j] = j + 1;
for (int i = 1; i <= m; i ++)
{
tmp[i][0] = tmp[i - 1][1];
for (int j = 1; j < MAXSIZE; j ++)
tmp[i][j] = tmp[i - 1][tmp[i][j - 1]];
}
return (tmp[m][n]);
/**************end************/
}
int main()
{
int m,n;
while(cin>>m>>n)
{
if(m==0&&n==0) break;
cout< 假设我们要计算Ackermann(2, 1),我们可以按照以下步骤进行计算:
- 初始化二维数组
tmp,行数为3,列数为MAXSIZE。 - 初始化第一列:
tmp[0][j] = j + 1,其中j从0到MAXSIZE-1。因此,tmp[0][0] = 1,tmp[0][1] = 2,tmp[0][2] = 3,以此类推。 - 计算
tmp[1][0]:根据Ackermann函数的定义,我们有tmp[1][0] = tmp[0][1] = 2。 - 计算
tmp[1][1]:根据Ackermann函数的定义,我们有tmp[1][1] = tmp[0][tmp[1][0]] = tmp[0][2] = 3。 - 计算
tmp[1][2]:根据Ackermann函数的定义,我们有tmp[1][2] = tmp[0][tmp[1][1]] = tmp[0][3] = 4。 - 计算
tmp[2][0]:根据Ackermann函数的定义,我们有tmp[2][0] = tmp[1][1] = 3。 - 计算
tmp[2][1]:根据Ackermann函数的定义,我们有tmp[2][1] = tmp[1][tmp[2][0]] = tmp[1][3] = 5。 - 最后,我们返回
tmp[2][1]的值,即得到了Ackermann(2, 1)的结果为5。
这个例子可以帮助你理解如何使用一个二维数组来计算Ackermann函数的值。需要注意的是,Ackermann函数的值增长速度非常快,因此在实际应用中需要使用高精度计算或者使用递归来计算较大的输入值。
第9关:递归求解单链表中的最大值
任务描述
本关任务:利用单链表表示一个整数序列,利用递归的方法求出单链表中整数的最大值。
编程要求
输入
多组数据,每组数据有两行,第一行为链表的长度n,第二行为链表的n个元素(元素之间用空格分隔)。当n=0时输入结束。
输出
对于每组数据分别输出一行,输出每个链表的最大值。
#include
using namespace std;
typedef struct LNode
{
int data;
struct LNode *next;
}LNode,*LinkList;
void CreateList_R(LinkList &L,int n)
{//后插法创建单链表
L=new LNode;
L->next=NULL;
LinkList r=L;
for(int i=0;i>p->data;
p->next=NULL;
r->next=p;
r=p;
}
}
int GetMax(LinkList L)
{//递归求解单链表中的最大值
/**************begin************/
int max;
if(L->next==NULL)
return L->data;
else
{
max=GetMax(L->next);
return L->data>=max?L->data:max;
}
/**************end************/
}
int main()
{
int n;
while(cin>>n)
{
if(n==0) break;
LinkList L;
CreateList_R(L,n);
L=L->next; //指向首元结点
cout< 在这段代码中,return L->data>=max?L->data:max; 将返回给调用该函数的上层调用者。这就是递归工作方式的核心。每次递归调用都会返回结果给上一层,直到到达链表的起始节点,然后结果返回给调用该函数的外部调用者。
例如,假设我们有一个链表,它的结构是这样的:
1 -> 2 -> 3 -> 4 -> 5
如果我们调用 GetMax(1),那么函数会递归地调用 GetMax(2)、GetMax(3)、GetMax(4) 和 GetMax(5)。在每一步中,它会比较当前节点的值和当前的最大值,并将较大的值赋给 max。在最后一个递归调用中,GetMax(5) 会返回最大值(在这个例子中是5)给 GetMax(4)。然后这个过程会逐级向上进行,直到 GetMax(1) 返回最大值给外部的调用者。
第10关:递归求解单链表中的结点个数
任务描述
本关任务:利用单链表表示一个整数序列,利用递归的方法计算单链表中结点的个数。
编程要求
输入
多组数据,每组数据有两行,第一行为链表的长度n,第二行为链表的n个元素(元素之间用空格分隔)。当n=0时输入结束。
输出
对于每组数据分别输出一行,对应链表中的各个结点个数。
#include
using namespace std;
typedef struct LNode
{
int data;
struct LNode *next;
}LNode,*LinkList;
void CreateList_R(LinkList &L,int n)
{//后插法创建单链表
L=new LNode;
L->next=NULL;
LinkList r=L;
for(int i=0;i>p->data;
p->next=NULL;
r->next=p;
r=p;
}
}
int GetLength(LinkList L)
{//递归求解单链表中的结点个数
/**************begin************/
if(!L->next) return 1; //L指向表尾,返回1
else return GetLength(L->next)+1; //每递归一次,结点数加1
/**************end************/
}
int main()
{
int n;
while(cin>>n)
{
if(n==0) break;
LinkList L;
CreateList_R(L,n);
L=L->next; //L指向首元结点
cout< 第11关:递归求解单链表中的平均值
任务描述
本关任务:利用单链表表示一个整数序列,利用递归的方法计算单链表中各个结点的平均值。
编程要求
输入
多组数据,每组数据有两行,第一行为链表的长度n,第二行为链表的n个元素(元素之间用空格分隔)。当n=0时输入结束。
输出
对于每组数据分别输出一行,对应链表中的各个结点的平均值,输出保留两位小数。
#include
using namespace std;
typedef struct LNode
{
int data;
struct LNode *next;
}LNode,*LinkList;
void CreateList_R(LinkList &L,int n)
{//后插法创建单链表
L=new LNode;
L->next=NULL;
LinkList r=L;
for(int i=0;i>p->data;
p->next=NULL;
r->next=p;
r=p;
}
}
double GetAverage(LinkList L,int n)
{//递归求解单链表中的平均值
/**************begin************/
if(!L->next) return L->data; //L指向表尾,返回其数值
else
{
double ave=GetAverage(L->next,n-1); //递归求解除尾结点外的其余n-1个结点的平均值
return (ave*(n-1)+L->data)/n; //返回平均值
}
/**************end************/
}
int main()
{
int n;
while(cin>>n)
{
if(n==0) break;
LinkList L;
CreateList_R(L,n);
L=L->next;//L指向首元结点
printf("%.2f\n",GetAverage(L,n));//输出保留两位小数
}
return 0;
} 第12关:中缀表达式转化为后缀表达式
任务描述
本关任务:输入一个中缀算术表达式,将其转换为后缀表达式。运算符包括+、-、*、/、(、)、=,参加运算的为小于10的自然数。(只考虑二元运算即可)
编程要求
输入
多组数据,每组数据一行,对应一个算术表达式,每个表达式均以“=”结尾。当表达式只有一个“=”时,输入结束。
输出
对于每组数据输出一行,为表达式的后缀式。
#include
using namespace std;
#define MAXSIZE 100
#define OK 1
#define ERROR 0
#define OVERFLOW -2
#define Status int
typedef struct
{
char *base;
char *top;
int stacksize;
}SqStack;
Status InitStack(SqStack &S)
{//初始化栈
S.base=new char[MAXSIZE];
if(!S.base) return OVERFLOW;
S.top=S.base;
S.stacksize=MAXSIZE;
return OK;
}
Status Push(SqStack &S, char e)
{//入栈
if(S.top-S.base==S.stacksize) //栈满
return ERROR;
*S.top=e;
S.top++;
return OK;
}
Status Pop(SqStack &S)
{//出栈
if(S.top==S.base) //栈空
return ERROR;
S.top--;
return OK;
}
char GetTop(SqStack S)
{//取栈顶元素
if(S.top!=S.base)
return *(S.top-1);
return ERROR;
}
char Precede(char a,char b)
{//比较符号优先级
if((a=='('&&b==')')||(a=='='&&b=='='))
return '=';
else if(a=='='||a=='('||b=='('||((a=='+'||a=='-')&&(b=='*'||b=='/')))
return '<';
else
return '>';
}
void InfixToSuffix(SqStack op,char s[])
{//将中缀表达式转化为后缀表达式并输出
/**************begin************/
for (int i = 0; s[i] != '\0'; i++) {
if ('0' <= s[i] && s[i] <= '9') {
cout << s[i]; // 如果是数字,则直接输出
} else {
while (1) {
if (Precede(GetTop(op), s[i]) == '<') {
Push(op, s[i]); // 如果栈顶操作符优先级小于当前操作符,将当前操作符压入栈中
break;
} else if (Precede(GetTop(op), s[i]) == '>') {
cout << GetTop(op); // 如果栈顶操作符优先级大于当前操作符,输出栈顶操作符并弹出
Pop(op);
} else {
Pop(op); // 如果栈为空,弹出栈中所有操作符
break;
}
}
}
}
cout << endl; // 输出换行符,表示转换完成
/**************end************/
}
int main()
{
SqStack op;
InitStack(op); //初始化字符栈op
Push(op,'='); //先在栈底放入'='便于以后比较符号优先级
char s[100];
while(cin>>s)
{
if(s[0]=='=')
break; //当表达式只有一个“=”时,输入结束
else
InfixToSuffix(op,s); //将中缀表达式转化为后缀表达式并输出
}
return 0;
} 解析:该函数将中缀表达式转化为后缀表达式。遍历输入字符串,如果是数字则直接输出;如果是操作符,则与栈顶操作符比较优先级,如果栈顶操作符优先级小于当前操作符,则将当前操作符压入栈中;如果栈顶操作符优先级大于当前操作符,则输出栈顶操作符并弹出;如果栈为空,说明所有操作数都已经被处理,退出循环。最后输出换行符,表示转换完成。