【数据结构】线段树
目录
- 1.概述
- 2.代码实现
-
- 2.1.聚合操作——求和
- 2.2.聚合操作——求和、求最小值、求最大值
- 3.应用
- 4.与前缀和之间的区别
更多数据结构与算法的相关知识可以查看数据结构与算法这一专栏。
1.概述
(1)线段树 (Segment Tree) 是一种二叉树形数据结构,经常用于高效地处理一维区间的各种查询和修改问题。
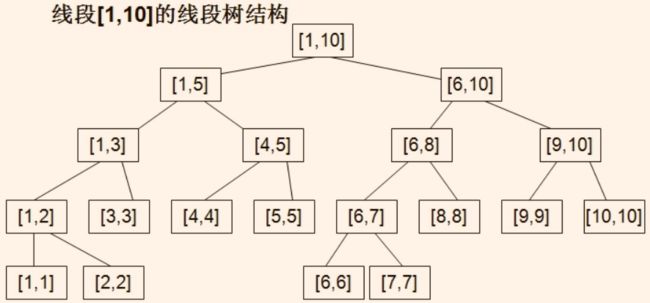
(2)一个线段树通常对应于一个区间,每个节点表示一个区间,具体如下图所示。
- 对于线段树中的每个节点,它有一个区间范围和一个值。
- 叶节点表示区间中的单个元素,而非叶子节点表示区间中的所有元素。
- 线段树的每个节点表示区间的一部分,其左子树表示左半部分区间,右子树表示右半部分区间。因此,线段树的叶节点数总是等于数据元素的个数,而线段树的高度为
⌈logn⌉ + 1,其中 n 为元素总个数。
① 上图来自线段树_百度百科。
② 一般来说,在代码中会用数组来存储某个区间内的元素,该数组内的元素可以是无序或者有序的,例如,nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 或者 nums = [2, 4, -1, 0, 9] 等。上图中线段树中的区间正好是前一个数组。
(3)线段树的主要优势是能够在 O(logn) 时间复杂度内执行区间查询(如最大值、最小值、区间和等)和区间修改操作(如区间加、区间减等),因此它非常适合解决那些需要频繁区间查询和修改的问题。
2.代码实现
(1)在线段树中,区间的聚合值是指该区间内元素的某种聚合操作的结果。这个聚合操作可以是求和、求最小值、求最大值等。聚合值的具体含义取决于所解决的问题,本节中分别给出以下两种情况。
(2)线段树的构建过程与 108.将有序数组转换为二叉搜索树这题类似,具体如下:
- 定义线段树节点:线段树是一种二叉树,每个节点代表一个区间。每个节点包含了该区间的起始点start、结束点end,以及其他你可能需要的附加信息。
- 定义递归构建函数:创建一个递归函数来构建线段树。该函数接收输入参数为当前节点、当前区间的起始点和结束点。
- 基本情况处理:对于当前节点,如果起始点和结束点相等,表示当前节点为叶子节点,直接返回。
- 划分区间:计算当前区间的中点 mid,将区间分割成两个子区间。通常是将区间一分为二,可以选择将 mid 设置为 (start+end)/2。
- 递归构建左子树和右子树:调用递归函数,传入左子树和右子树的起始点和中点以构建左右子树。
- 合并信息:在递归回溯时,将左右子树的信息合并到当前节点。这通常取决于你的问题需求,可以是求和、求最大值、求最小值等。
- 返回根节点:递归构建完成后,返回根节点。
2.1.聚合操作——求和
(1)实现区间求和操作(包括修改区间的某个元素)的代码实现如下:
class SegmentTree {
//线段树数组,segmentTree[i] 表示线段树的第 i 个节点(区间)的聚合值,本代码中是区间和
int[] segmentTree;
//原始数组
int[] nums;
public SegmentTree(int[] nums) {
this.nums = nums;
int n = nums.length;
//确定树的高度
int height = (int) (Math.ceil(Math.log(n) / Math.log(2))) + 1;
//根据树的高度计算需要的线段树数组大小
int maxSize = (int) Math.pow(2, height) - 1;
//创建线段树数组
segmentTree = new int[maxSize];
//构建线段树
buildTree(0, 0, n - 1);
}
//构建线段树
private int buildTree(int index, int start, int end) {
//叶子节点
if (start == end) {
//叶子节点存储对应的原始数组值
segmentTree[index] = nums[start];
return segmentTree[index];
}
int mid = start + (end - start) / 2; // 计算中间位置
//分别递归构建左子树和右子树
segmentTree[index] = buildTree(2 * index + 1, start, mid) +
buildTree(2 * index + 2, mid + 1, end);
return segmentTree[index];
}
//更新原始数组中的某个元素,并同时更新线段树
public void update(int i, int val) {
//计算变化的差值
int diff = val - nums[i];
//更新原始数组中的值
nums[i] = val;
//更新线段树
updateTree(0, 0, nums.length - 1, i, diff);
}
//更新线段树
private void updateTree(int index, int start, int end, int i, int diff) {
if (i < start || i > end) {
//该节点不包含要更新的元素,直接返回
return;
}
//更新当前节点的值
segmentTree[index] += diff;
if (start != end) {
//计算中间位置
int mid = start + (end - start) / 2;
//递归更新左子树
updateTree(2 * index + 1, start, mid, i, diff);
//递归更新右子树
updateTree(2 * index + 2, mid + 1, end, i, diff);
}
}
//查询线段树中某个区间的和
public int querySum(int left, int right) {
return queryTree(0, 0, nums.length - 1, left, right);
}
// 查询线段树
private int queryTree(int index, int start, int end, int left, int right) {
if (left > end || right < start) {
//区间不相交,返回 0
return 0;
}
if (left <= start && right >= end) {
//当前节点表示的区间完全被查询区间包含,直接返回当前节点的值
return segmentTree[index];
}
//计算中间位置
int mid = start + (end - start) / 2;
//分别递归查询左子树和右子树
return queryTree(2 * index + 1, start, mid, left, right) +
queryTree(2 * index + 2, mid + 1, end, left, right);
}
}
(2)测试代码如下:
class SegmentTreeTest {
public static void main(String[] args) {
//原始数组,可以是有序或者无序的
int[] nums = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
SegmentTree segmentTree = new SegmentTree(nums);
//查询区间 [1, 4] 的和,即 nums[1...4] 的和
int sum = segmentTree.querySum(1, 4);
System.out.println("Sum of range [1, 4]: " + sum);
//将数组下标为 2 的元素更新为 6,即更新 nums[2] = 6,同时更新线段树
segmentTree.update(2, 6);
//再次查询区间 [1, 4] 的和
sum = segmentTree.querySum(1, 4);
System.out.println("Updated sum of range [1, 4]: " + sum);
}
}
输出结果如下:
Sum of range [1, 4]: 14
Updated sum of range [1, 4]: 17
2.2.聚合操作——求和、求最小值、求最大值
(1)实现区间求和、求最小值、求最大值操作(包括修改区间的某个元素)的代码实现如下:
class SegmentTree {
private Node root;
//定义节点类,用于表示某个区间
private class Node {
int start;
int end;
int sum;
int max;
int min;
Node left;
Node right;
Node(int start, int end) {
this.start = start;
this.end = end;
this.sum = 0;
this.max = Integer.MIN_VALUE;
this.min = Integer.MAX_VALUE;
}
}
public SegmentTree(int[] nums) {
this.root = build(nums, 0, nums.length - 1);
}
//构建线段树
private Node build(int[] nums, int start, int end) {
if (start > end) {
return null;
}
Node node = new Node(start, end);
if (start == end) {
node.sum = nums[start];
node.max = nums[start];
node.min = nums[start];
} else {
int mid = start + (end - start) / 2;
node.left = build(nums, start, mid);
node.right = build(nums, mid + 1, end);
node.sum = node.left.sum + node.right.sum;
node.max = Math.max(node.left.max, node.right.max);
node.min = Math.min(node.left.min, node.right.min);
}
return node;
}
//查询线段树中某个区间的和
public int queryRangeSum(int start, int end) {
return queryRangeSum(root, start, end);
}
private int queryRangeSum(Node node, int start, int end) {
if (node.start == start && node.end == end) {
return node.sum;
}
int mid = node.start + (node.end - node.start) / 2;
if (end <= mid) {
return queryRangeSum(node.left, start, end);
} else if (start > mid) {
return queryRangeSum(node.right, start, end);
} else {
return queryRangeSum(node.left, start, mid) + queryRangeSum(node.right, mid + 1, end);
}
}
//查询线段树中某个区间的最大值
public int queryRangeMax(int start, int end) {
return queryRangeMax(root, start, end);
}
private int queryRangeMax(Node node, int start, int end) {
if (node.start == start && node.end == end) {
return node.max;
}
int mid = node.start + (node.end - node.start) / 2;
if (end <= mid) {
return queryRangeMax(node.left, start, end);
} else if (start > mid) {
return queryRangeMax(node.right, start, end);
} else {
return Math.max(queryRangeMax(node.left, start, mid),
queryRangeMax(node.right, mid + 1, end));
}
}
//查询线段树中某个区间的最小值
public int queryRangeMin(int start, int end) {
return queryRangeMin(root, start, end);
}
private int queryRangeMin(Node node, int start, int end) {
if (node.start == start && node.end == end) {
return node.min;
}
int mid = node.start + (node.end - node.start) / 2;
if (end <= mid) {
return queryRangeMin(node.left, start, end);
} else if (start > mid) {
return queryRangeMin(node.right, start, end);
} else {
return Math.min(queryRangeMin(node.left, start, mid),
queryRangeMin(node.right, mid + 1, end));
}
}
//更新原始数组中的某个元素,并同时更新线段树
public void update(int index, int value) {
update(root, index, value);
}
private void update(Node node, int index, int value) {
if (node.start == node.end) {
node.sum = value;
node.max = value;
node.min = value;
return;
}
int mid = node.start + (node.end - node.start) / 2;
if (index <= mid) {
update(node.left, index, value);
} else {
update(node.right, index, value);
}
node.sum = node.left.sum + node.right.sum;
node.max = Math.max(node.left.max, node.right.max);
node.min = Math.min(node.left.min, node.right.min);
}
}
(2)测试代码如下:
class SegmentTreeTest {
public static void main(String[] args) {
//原始数组,可以是有序或者无序的
int[] nums = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
SegmentTree segmentTree = new SegmentTree(nums);
//查询区间 [1, 4] 的和,即 nums[1...4] 的和
int sum = segmentTree.queryRangeSum(1, 4);
System.out.println("Sum of range [1, 4]: " + sum);
int max = segmentTree.queryRangeMax(1, 4);
System.out.println("Max of range [1, 4]: " + max);
int min = segmentTree.queryRangeMin(1, 4);
System.out.println("Min of range [1, 4]: " + min);
//将数组下标为 1 的元素更新为 0,即更新 nums[1] = 0,同时更新线段树
segmentTree.update(1, 0);
//将数组下标为 2 的元素更新为 6,即更新 nums[2] = 6,同时更新线段树
segmentTree.update(2, 6);
//再次查询区间 [1, 4] 的和
sum = segmentTree.queryRangeSum(1, 4);
System.out.println("Updated sum of range [1, 4]: " + sum);
max = segmentTree.queryRangeMax(1, 4);
System.out.println("Updated Sum of range [1, 4]: " + max);
min = segmentTree.queryRangeMin(1, 4);
System.out.println("Updated Min of range [1, 4]: " + min);
}
}
输出结果如下:
Sum of range [1, 4]: 14
Max of range [1, 4]: 5
Min of range [1, 4]: 2
Updated sum of range [1, 4]: 15
Updated Sum of range [1, 4]: 6
Updated Min of range [1, 4]: 0
3.应用
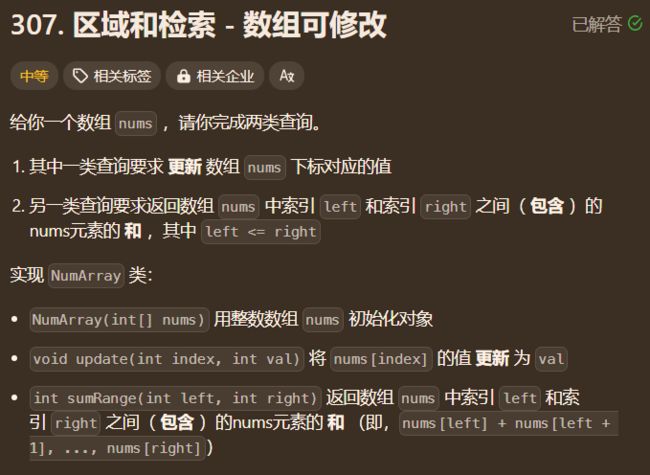
(1)LeetCode 中的 307.区域和检索 - 数组可修改这题便是对线段树的具体应用,其题目如下。显然,使用上面的代码可以直接求解。
(2)大家可以去 LeetCode 上找相关的线段树的题目来练习,或者也可以直接查看 LeetCode 算法刷题目录 (Java) 这篇文章中的线段树章节。如果大家发现文章中的错误之处,可在评论区中指出。
4.与前缀和之间的区别
(1)线段树和前缀和是两种常见的用于解决区间查询问题的数据结构,它们有一些区别:
- 数据结构:
- 线段树是一种二叉树结构,用于处理区间查询和更新操作。它将区间划分为不相交的子区间,并将每个子区间的信息存储在相应节点中。
- 前缀和是一个数组,用于存储前缀和值。它通过计算数组元素累加和的方式存储数据。
- 功能:
- 线段树可以支持多种区间查询操作,例如区间和、区间最大值、区间最小值等。它可以在 O(logN) 的时间复杂度内完成查询和更新操作。
- 前缀和主要用于计算数组中特定区间的和。它可以在 O(1) 的时间内计算出给定区间的和,但只能处理区间和的查询。
- 空间复杂度:
- 线段树的空间复杂度为 O(N),其中 N 是数组的大小。它需要存储整个线段树的节点。
- 前缀和的空间复杂度为 O(N),其中 N 是数组的大小。它只需要存储一个与数组大小相等的前缀和数组。
- 应用场景:
- 线段树通常用于解决需要频繁进行区间查询和更新操作的问题,比如计算数组的区间和、区间最大值和最小值等。
- 前缀和通常用于解决需要频繁计算数组特定区间和的问题,比如计算子数组的和、快速判断数组中是否存在某个区间的和等。
(2)综上所述,线段树和前缀和在功能和应用场景上略有不同,选择使用哪种数据结构取决于具体的问题需求和效率要求。
有关前缀和的相关知识可以参考【数据结构】前缀和数组这篇文章。