生成式深度学习(第二版)-译文-第四章-生成对抗网络
章节目标
- 了解生成对抗网络(GAN)的架构设计;
- 利用Keras 从零开始训练一个深度卷积 GAN (DCGAN)。
- 利用DCGAN来生成新的图像。
- 理解训练DCGAN时面临的常见问题。
- 了解Wasserstein GAN(WGAN)架构如何解决上述问题。
- 理解WGAN可以添加的额外改进,例如融合梯度惩罚(Gradient Penalty, GP)项到损失函数。
- 利用Keras 从零开始构建WGAN-GP。
- 利用WGAN-GP来生成新的图像。
- 了解条件GAN(CGAN)如何让我们具备基于给定标签条件生成输出的能力。
- 在Keras中如何构建CGAN并用它来操纵生成图像。
在2014年,Ian Goodfellow等在蒙特利尔的NeurIPS大会上提出了一篇论文,标题为《Generative Adversarial Nets》。生成对抗网络(或者更广为人知的名称 GANs)的引入现在普遍被认为是生成式建模历史上的一个关键转折点。因为本篇文章提出的核心思想直接启发了迄今为止的多个成功的生成式模型。
本章将首先给出GANs的理论基础,然后我们再看看如何使用Keras构建我们自己的GANs。
引言
让我们以一则短故事来介绍GAN训练过程中的一些基础概念。
| 布鲁克积木和伪造者 |
|---|
| 今天是你作为Brickki公司质量控制主管的第一天,该公司专注于生产各种形状和尺寸的高质量积木(如下图4-1所示)。很快,有人提醒你,生成线下来的物品存在一个问题。有一个竞对开始仿制布鲁克积木,并且找到了一个方法将仿制积木混到你们公司消费者的袋子里。你决定成为一个辨别布鲁克积木正品和仿制品的专家,这样你就能在产线上拦截伪造的积木,避免它们进入终端用户受众。随着时间的推移,吸收用户的反馈之后,你越来越清楚该如何区分正品和仿制品。 |
| 伪造者对此并不开心 — 他们对你不断提高的检测能力做出反应了 — 在仿制过程中做出一些改变,让正品积木和仿制积木的差别更小,从而让你更加难以区分。 |
| 没人放弃,你重新训练自己,以便能够识别更复杂的伪造,并时刻保持比伪造者领先一步。 这个过程一直持续,伪造者持续改进积木制造工艺,你尝试不断精进仿制品鉴定技术。 |
| 随着时间的流逝,人们越来越难鉴别布鲁克正品积木和仿制品了。看起来,这个简单的猫鼠游戏对于提升仿制品质量和检测质量都有重大影响。 |
上面这个布鲁克积木和仿造者的故事描述了生成对抗网络的训练过程。
生成对抗网络是两个相反过程的斗争,一为生成器,一为鉴别器。生成器尝试将随机噪声转换成一个观察,使得其看起来好像是从原始数据集中采样而来,鉴别器则努力判定一个观察到底是来自原始数据库还是生成器的仿制。输入和输出的样例如下图4-2所示。

作为这一过程的开始,生成器输出噪声图像,鉴别器随机预测。GANs的关键在于我们如何交替训练这两个网络, 使得: 生成器越来越擅长骗过鉴别器,鉴别器越来越擅长正确区分仿制品。这驱动着生成器不断寻找新的方式来骗过鉴别器,因此整个过程能够持续。
深度卷积GAN(DCGAN)
让我们以Keras中构建第一个GAN作为开始,来生成伪造的积木图片。
我们将紧密跟踪GANs领域的一篇主要论文 “Unsupervised Representation Learning with Deep Convolutional Generative Adversial Networks.” 在这篇2015年的工作中,作者给出了如何构建一个深度卷积GAN来从不同数据库生成真实感的图像。它们也介绍了一些改动来显著提升生成图像的质量。
| 运行本示例代码 |
|---|
| 本示例代码可以在Jupyter Notebook的如下位置找到: “notebooks/04_gan/01_dcgan/dcgan.ipynb” |
Bricks数据集
首先,你需要下载训练数据。我们将使用Kaggle的LEGO Bricks数据集图像。这是计算机渲染数据集,包含50个不同玩具积木各个视角拍摄的近4万照片。

我们可以利用本书代码库中的 Kaggle 数据集下载器脚本来下载这一数据集,如下样例4-1所示。它会将数据集和伴随的metadata本地下载到 /data 目录。
bash scripts/download_kaggle_data.sh joosthazelzet lego-brick-images
我们使用Keras函数 image_dataset_from_directory 来构建一个TensorFlow数据集指向图片存储的位置,如下示例4-2所示。这允许我们在需要时(例如训练)成批将图像读取到内存中,使得我们可以操作大的数据集,并且不用担心如何将整个数据集放到内存中。同时,我们也通过像素插值将图像放缩到64x64。
train_data = utils.image_dataset_from_directory(
"/app/data/lego-bricks-images/dataset",
labels = None,
color_mode = "grayscale",
image_size = (64,64),
batch_size = 128,
shuffle = True,
seed = 42,
interpolation = "bilinear",
)
原始的数据其取值范围在[0,255]。当训练GANs时,我们将数据放缩到[-1,1],使得我们可以在生成器最后一层上使用 tanh 激活函数,因为tanh相对于sigmoid函数能提供更强的梯度。
def preprocess(img):
img = (tf.cast(img, "float32") - 127.5 ) / 127.5
return img
train = train_data.map(lambda x: preprocess(x))
鉴别器
鉴别器的目标是预测一幅图像是真实还是伪造。这是一个有监督图像分类问题,因此我们可以使用一个第二章中类似的架构: 堆叠卷积层+单一输出节点。
表4-1列出了我们将要构建之鉴别器的完整架构。
| 层(类型) | 输出形状 | 参数数量 |
|---|---|---|
| InputLayer | (None, 64, 64, 1) | 0 |
| Conv2D | (None, 32, 32, 64) | 1024 |
| LeakyReLU | (None, 32, 32, 64) | 0 |
| Dropout | (None, 32, 32, 64) | 0 |
| Conv2D | (None, 16, 16, 128) | 131072 |
| BatchNormalization | (None, 16, 16, 128) | 512 |
| LeakyReLU | (None, 16, 16, 128) | 0 |
| Dropout | (None, 16, 16, 128) | 0 |
| Conv2D | (None, 8, 8, 256) | 524288 |
| BatchNormalization | (None, 8, 8, 256) | 1024 |
| LeakyReLU | (None, 8, 8, 256) | 0 |
| Dropout | (None, 8, 8, 256) | 0 |
| Conv2D | (None, 4, 4, 512) | 2097152 |
| BatchNormalization | (None, 4, 4, 512) | 2048 |
| LeakyReLU | (None, 4, 4, 512) | 0 |
| Dropout | (None, 4, 4, 512) | 0 |
| Conv2D | (None, 1, 1, 1) | 8192 |
| Flatten | (None, 1) | 0 |
| 所有参数 | 2765312 |
|---|---|
| 训练参数 | 2763520 |
| 非训练参数 | 1792 |
用以构建鉴别器的Keras 代码如下示例4-4所示。
discriminator_input = layers.Input(shape=(64,64,1))
x = layers.Conv2D(64, kernel_size = 4, strides = 2, padding = "same", use_bias = False)(discriminator_input)
x = layers.LeakyReLU(0.2)(x)
x = layers.Dropout(0.3)(x)
x = layers.Conv2D(128, kernel_size = 4, strides = 2, padding = "same", use_bias = False)(x)
# moving_mean = moving_mean * momentum + batch_mean * (1 - momentum)
# moving_var = moving_var * momentum + batch_var * (1 - momentum)
# 式中的 momentum 为动量参数
x = layers.BatchNormalization(momentum = 0.9)(x) # 滑动平均
x = layers.LeakyReLU(0.2)(x)
x = layers.Dropout(0.3)(x)
x = layers.Conv2D(256, kernel_size = 4, strides = 2, padding = "same", use_bias = False)(x)
x = layers.BatchNormalization(momentum = 0.9)(x) # 滑动平均
x = layers.LeakyReLU(0.2)(x)
x = layers.Dropout(0.3)(x)
x = layers.Conv2D(512, kernel_size = 4, strides = 2, padding = "same", use_bias = False)(x)
x = layers.BatchNormalization(momentum = 0.9)(x) # 滑动平均
x = layers.LeakyReLU(0.2)(x)
x = layers.Dropout(0.3)(x)
x = layers.Conv2D(1, kernel_size = 4, strides = 1, padding = "valid", use_bias = False, activation = 'sigmoid')(x)
# 经过上步操作,输出的张量形状为1x1x1,直接拉直即可,无需最后一个Dense层
discriminator_output = layers.Flatten()(x)
# 定义鉴别器之 Keras model --- 模型接受一张输入图像,输出一个0到1之间的数
discriminator = models.Model(discriminator_input, discriminator_output)
注意我们如何在Conv2D层中使用 stride = 2 来减少张量的空间尺寸(原图64,随后32,16,8,4, 最终1), 同时逐渐增大通道数 (灰度输入1,然后64,128, 256,最终512),最终坍缩为单一预测。
我们在最后的Conv2D上使用了一个sigmoid激活来输出一个0到1的数字。
生成器
现在,让我们一起来构建生成器。生成器的输入是一个从多维正态分布中拉取的向量。输出是一幅与原始图像训练数据相同尺寸的图像。
这个描述也许让你回忆起变分自编码器中的解码器。事实上,GAN中的生成器与VAE中的解码器目标完全相同: 将隐空间的一个编码转换为一幅图像。在生成式建模中,将隐空间映射回原始域是非常常见的概念,因为它给与我们通过操纵隐空间向量来改变原始域中高层图像特征的能力。
我们将构建的生成器架构如表4-2所示。
| 层(类型) | 输出形状 | 参数数量 |
|---|---|---|
| InputLayer | (None, 100) | 0 |
| Reshape | (None, 1,1,100) | 0 |
| Conv2DTranspose | (None, 4, 4, 512) | 819200 |
| BatchNormalization | (None, 4, 4, 512) | 2048 |
| ReLU | (None, 4, 4, 512) | 0 |
| Conv2DTranspose | (None, 8, 8, 256) | 2097152 |
| BatchNormalization | (None, 8, 8, 256) | 1024 |
| ReLU | (None, 8, 8, 256) | 0 |
| Conv2DTranspose | (None, 16, 16, 128) | 524288 |
| BatchNormalization | (None, 16, 16, 128) | 512 |
| ReLU | (None, 16, 16, 128) | 0 |
| Conv2DTranspose | (None, 32, 32, 64) | 131072 |
| BatchNormalization | (None, 32, 32, 64) | 256 |
| ReLU | (None, 32, 32, 64) | 0 |
| Conv2DTranspose | (None, 64, 64, 1) | 1024 |
| 所有参数 | 3576576 |
|---|---|
| 训练参数 | 3574656 |
| 非训练参数 | 1920 |
用以构建生成器的Keras 代码如下示例4-5所示。
generator_input = layers.Input(shape=(100,))
x = layer.Reshape((1,1,100))(generator_input)
x = layers.Conv2DTranspose(512, kernel_size = 4, strides = 1, padding = "valid", use_bias = False)(x)
x = layers.BatchNormalization(momentum = 0.9)(x) # 滑动平均
x = layers.LeakyReLU(0.2)(x)
x = layers.Conv2DTranspose(256, kernel_size = 4, strides = 2, padding = "same", use_bias = False)(x)
x = layers.BatchNormalization(momentum = 0.9)(x) # 滑动平均
x = layers.LeakyReLU(0.2)(x)
x = layers.Conv2DTranspose(128, kernel_size = 4, strides = 2, padding = "same", use_bias = False)(x)
x = layers.BatchNormalization(momentum = 0.9)(x) # 滑动平均
x = layers.LeakyReLU(0.2)(x)
x = layers.Conv2DTranspose(64, kernel_size = 4, strides = 2, padding = "same", use_bias = False)(x)
x = layers.BatchNormalization(momentum = 0.9)(x) # 滑动平均
x = layers.LeakyReLU(0.2)(x)
# 最终的Conv2DTranspose层使用了tanh激活函数,从而将输出约束到[-1,1]范围,以符合原始的图像域
generator_output = layers.Conv2DTranspose(1, kernel_size = 4, strides = 2, padding = "same", use_bias = False, activation = "tanh")(x)
# 定义生成器之 Keras model --- 模型接受一个100维向量,输出一个[64,64,1]张量
generator = models.Model(generator_input, generator_output)
注意我们如何在Conv2DTranspose层中使用stride=2来增加张量的空间形状(原始向量1,然后4,8,16, 32, 最终64), 同时减少通道数(512,然后256,128,64,最后1来匹配灰度输出)。
| 上采样 vs Conv2Transpose |
|---|
| Conv2DTranspose层有一个替代: 使用UpSampling2D层紧接Conv2D层(stride=1), 如样例4-6所示。 |
x = layers.UpSampling2D(size = 2)(x) |
x = layers.Conv2D(256, kernel_size = 4, strides = 1, padding = "same")(x) |
| Upsampling2D层简单的进行行列重复以在尺寸上翻倍。Conv2D层(strides=1)执行卷积操作。这与卷积transpose类似,但是卷积transpose使用0来填充像素间空缺,upsampling则重复已有的像素值。 |
| 目前,已知Conv2DTranspose方法会在输出图像中产生artifacts,或者小的棋盘格模式(如图4-4所示),破坏输出的质量。但是,它们仍然在很多有影响力的GANs文献中被使用,并且在深度学习实践工具箱中一直是强有力的工具。 |
| Upsampling + Conv2D 以及 Conv2DTranspose 两种方式都是将张量变换回图像域的可行方式。到底采用哪种方法,完全取决于你的问题设定,以及两种方法的实际效果。 |
DCGAN的训练
我们将看到,在DCGAN中,生成器和鉴别器的架构非常简单,其实与第三章中我们看到的VAE方法并没有大的不同。理解GANs的关键在于理解生成器和鉴别器的训练过程。
我们可以这样训练一个鉴别器: 构建一个训练集,其中一些图像是来自训练集的真实观察,另一些是生成器的虚假输出。然后,我们将这个作为一个有监督学习问题,其中真实图像标签为1,虚假图像标签为0,二元互熵作为损失函数。
我们该如何训练生成器呢?我们需要找到一个方法对生成图像进行打分,使得生成器可以朝着更高分数的方向优化。幸运的是,我们恰好有鉴别器来做这个事!我们可以生成一批图像,并且将它们传递给鉴别器,得到每个图形的分数。生成器的损失函数可以简单设定为这些概率与全1向量的二元互熵,因为我们想训练的生成器,能生成的图像必须能骗过鉴别器。
关键在于,我们需要在这两个网络的训练过程中切换,确保每次我们只迭代一个网络的权重。例如,在生成器训练过程中,只有生成器的权重被更新。如果我们同时也允许鉴别器的权重被挑战,那么鉴别器会做自我调整使得它尽可能的将生成图像预测为真,而这并不是我们想要的。我们希望生成图像之预测尽可能接近1(真) 完全是因为生成器是强大的,而非因为鉴别器是弱小的。
鉴别器和生成器的训练过程框图如下图4-6所示。

Keras提供给我们构建 train_step 函数的能力来实现这个逻辑。样例4-7给出了完整的DCGAN模型类。
class DCGAN(models.Model):
def __init__(self, discriminator, generator, latent_dim):
super(DCGAN, self).__init__()
self.discriminator = discriminator
self.generator = generator
self.latent_dim = latent_dim
def compile(self, d_optimizer, g_optimizer):
super(DCGAN, self).compile()
# 生成器和鉴别器的损失函数为BinaryCrossentropy()
self.loss_fn = loss.BinaryCrossentropy()
self.d_optimizer = d_optimizer
self.g_optimizer = g_optimizer
self.d_loss_metric = metrics.Mean(name="d_loss")
self.g_loss_metric = metrics.Mean(name="g_loss")
@property
def metrics(self):
return [self.d_loss_metric, self.g_loss_metric]
def train_step(self, real_images):
batch_size = tf.shape(real_images)[0]
# 要训练生成器和鉴别器网络,首先从多元标准正态中采样一批向量
random_latent_vectors = tf.random.normal(shape=(batch_size, self.latent_dim))
with tf.GradientTape() as gen_tape, tf.GradientTape() as disc_tape:
# 向量传给生成器生成一批图像
generated_images = self.generator(random_latent_vectors, training = True)
# 让鉴别器判断生成图像是否为真
real_predictions = self.discriminator(real_images, training = True)
fake_predictions = self.discriminator(generated_images, training = True)
real_labels = tf.ones_like(real_predictions)
real_noisy_labels = real_labels + 0.1 * tf.random.uniform(tf.shape(real_predictions))
fake_labels = tf.ones_like(fake_predictions)
fake_noisy_labels = fake_labels - 0.1 * tf.random.uniform(tf.shape(fake_predictions))
d_real_loss = self.loss_fn(real_noisy_labels, real_predictions)
d_fake_loss = self.loss_fn(fake_noisy_labels, fake_predictions)
# 鉴别器损失是 真实图像(标签为1) 和 伪图像(标签为0) 的二元互熵之平均
d_loss = (d_real_loss + d_fake_loss) / 2.0
# 生成器损失是 鉴别器在生成图像上预测结果和全1标签的二元互熵
g_loss = self.loss_fn(real_labels, fake_predictions
gradients_of_discriminator = disc_tape.gradient(d_loss, self.discriminator.trainable_variables)
gradients_of_generator = disc_tape.gradient(g_loss, self.generator.trainable_variables)
# 分别更新生成器和鉴别器权重
self.d_optimizer.apply_gradients(zip(gradients_of_discriminator, discriminator.trainable_variables))
self.g_optimizer.apply_gradients(zip(gradients_of_generator, generator.trainable_variables))
self.d_loss_metric.update_state(d_loss)
self.g_loss_metric.update_state(g_loss)
return {m.name: m.result() for m in self.metrics}
dcgan = DCGAN(discriminator = discriminator, generator=generator, latent_dim = 100)
dcgan.compile(
d_optimizer=optimizer.Adam(learning_rate=0.0002, beta_1 = 0.5, beta_2 = 0.999),
g_optimizer=optimizer.Adam(learning_rate=0.0002, beta_1 = 0.5, beta_2 = 0.999),
)
dcgan.fit(train, epochs=300)
鉴别器和生成器一直在竞争主动权,这会导致DCGAN的训练过程不稳定。理想情况下,训练过程会找到一个均衡: 既允许生成器从鉴别器处学到有意义的信息,使得生产图像质量上升。经过足够多的epochs,鉴别器倾向于结束主导,如图4-6所示,但这个不是大的问题,因为生成器这时很可能已经学会了如何产生足够高质量图像。

| 在标签中加入噪声 |
|---|
| 训练GAN时一个有用的trick是: 在训练标签中加入少量的随机噪声。这有助于增强训练过程的稳定性,并让生成的图像更加锐利。标签平滑作为驯服鉴别器的一种手段,使得鉴别器面临更挑战的任务,不至于压倒生成器。 |
DCGAN分析
通过观察生成器在训练特定轮次的生成图像(图4-7),很显然生成器生成的图像越来越像从训练集中抽取出来的。

一个神经网络可以将随机噪声转换成有意义的东西,这看起来真实奇迹!值得注意的是,对于模型的训练,我们除了裸像素并未提供任何多余的信息,因此它必定是仔细学会了一些高层次的概念,例如如何画阴影,长方体,圆等等。
要得到成功生成式模型的另一个要求是它所做的不是简单复制训练集中的图像。为了验证这一点,对于一个特定生成图像,我们可以找出训练集中最接近的图像。距离的一个好度量是L1距离,定义如下:
def compare_images(img1, img2):
return np.mean(np.abs(img1, img2))
图4-8给出了一组生成图像在训练集中的最相似样本。我们可以看到尽管生成图像和训练集有一定程度的相似性,但他们并不完全相同。这表明,生成器理解了高层次特征,可以生成与其所见过完全不同的样本。

GAN训练: 建议和技巧
尽管GANs时生成式建模的一大主要突破技术,它们却以难于训练而臭名昭著。在这一小节,我们将探索GANs训练过程中一些常见的问题和挑战,以及潜在的解决办法。在下一小节中,我们将看到一些对于GAN框架的基础性调整,使得我们可以修正这些问题。
鉴别器压倒生成器
如果鉴别器变得过强,从损失函数反传的信号太弱,以至于不能驱使生成器做出有意义的改进。在最坏的情况下,鉴别器完美的学会了如何区分真实图像和伪造图像,梯度完全消失,导致无法训练,如图4-9所示。

如果你发现鉴别器损失函数塌陷,就需要找到一些方法来弱化鉴别器。可以尝试如下建议:
- 增大鉴别器 Dropout层的 rate参数了来抑制网络中流动的信息;
- 减少鉴别器的学习率。
- 减少鉴别器重卷积滤波器个数。
- 在训练鉴别器时在标签中添加噪声。
- 训练鉴别器时随机将一些样本进行标签翻转。
生成器压倒鉴别器
如果鉴别器不足够强大,生成器将很容易用一小撮近似相同的样本糊弄鉴别器。这被称为模式坍塌(mode collapse)。
例如,如果我们想在几批样本上训练生成器,而并不更新鉴别器。生成器将会倾向于找到单个观察(也被成为mode),该观察始终能糊弄鉴别器,并开始将隐空间中的每个点都影射到这个观察图像上。更进一步的,损失函数的梯度会坍塌到近乎0,因此无法从这个状态中恢复。
即使我们努力尝试重新训练鉴别器来阻止它被单一的点糊弄,生成器也只会找到另外一个mode来糊弄鉴别器,因为它已经对于输入麻木了,因此并无动力来产生多样的输出。
模式坍塌效应如下4-10所示。

如果你发现生成器正在遭受模式坍塌,你可以尝试采用与上一小节中建议相反的策略来加强鉴别器。另外,你也可以减小两个网络的学习率,并增加batch size。
无信息损失
因为深度学习模型瞄准损失函数的最小化,我们很自然认为:生成器损失越小,生成的图像质量也就越好。但是,因为生成器仅仅根据当前的鉴别器打分,同时,鉴别器也在持续改进。因此,我们无法在训练过程的不同点上比较损失函数。事实上,在图4-6中,随着时间的迁移,尽管生成的图像质量明显改进,生成器的损失函数实际上在增加。生成器损失和图像质量之间关联的确实有时候让GAN的训练难于监督。
超参数
我们已经看到,即使是简单的GANs,都有一大堆超参数要调。除了鉴别器和生成器的整体架构之外,还有一系列主导参数,包括batch normalization,dropout, learning rate, activation layers,卷积滤波器,核大小,striding, batch size,以及隐空间尺寸。GANs对所有这些参数的细微变化都非常敏感,找到一组有效参数很多时候是试错的结果,并无定则可以遵循。
这也是为什么理解GAN的内在工作机理及损失函数的解释如此重要,只有理解了,我们才可以进行有意义的超参调整,使得模型的稳定性得到提升。
解决GAN的挑战
近年来,一些关键的改进极大提升了GAN模型整体的稳定性,并消除了前面列出来的一些问题,如模式坍塌。
本章剩下的部分里,我们将检查 Wasserstein GAN with Gradient Penalty (WGAN-GP), 这包含了我们已经讨论的几种GAN框架调整基数,可以帮助提升稳定性,改进图像生成质量。
带梯度惩罚的Wasserstein GAN (WGAN-GP)
在这一小节中,我们将构建一个WGAN-GP,来从CelebA数据集(第三章中已经使用过)中生成人脸。
| 运行示例代码 |
|---|
| 本示例代码可以在Jupyter Notebook的以下路径找到: “notebooks/04_gan/02_wgan_gp/wgan_gp.ipynb”。这部分代码修改自Keras官网上Aakash Kumar Nain的杰出WGAN-GP教程。 |
Wasserstein GAN (WGAN), 首次提出于Arjovsky等人在2017年发表的论文,它是推动GAN训练走向稳定的第一个里程碑。通过一系列改进,作者可以训练出具备以下两个特性的GAN(引自原文):
- 一个有用的损失度量,可以将生成器收敛性 和 样本质量关联起来。
- 优化过程具备更强的稳定性。
特别的,论文对于生成器和鉴别器引入了Wasserstein损失函数。通过抛弃之前的二元互熵损失函数,使用Wasserstein损失函数带来了更稳定的GAN收敛结果。
在本小节中,我们将定义Wasserstein损失函数,然后一起看看我们还需要针对模型结构和训练过程做出哪些改变来适配新的损失函数。
整个模型类在Jupyter Notebook的如下位置可以找到: “chapter05/wgan-gp/faces/train.ipynb”.
Wasserstein 损失
首先,我们回顾一下二元互熵损失的定义 — 我们当前用来训练GAN鉴别器和生成器之损失函数。
− 1 n ∑ i = 1 n ( y i l o g ( p i ) + ( 1 − y i ) l o g ( 1 − p i ) ) -\frac{1}{n}\sum_{i=1}^n (y_i log (p_i) + (1 - y_i)log (1 - p_i)) −n1∑i=1n(yilog(pi)+(1−yi)log(1−pi))
为了训练GAN中的鉴别器D,我们计算如下损失: 比较真实图像之预测 p i = D ( X i ) p_i=D(X_i) pi=D(Xi) 与响应 y i = 1 y_i=1 yi=1,以及比较生成图像之预测 p i = D ( G ( z i ) ) p_i=D(G(z_i)) pi=D(G(zi))与响应 y i = 0 y_i=0 yi=0. 因此,对GAN的鉴别器而言,最小化损失函数可以写作如下式4-2:
min D − ( E x ∼ p x [ l o g D ( x ) ] + E z ∼ p z [ l o g ( 1 − D ( G ( z ) ) ) ] ) \min \limits_{D} -(\mathbb{E}_{x \sim p_x} [log D(x)] + \mathbb{E}_{z \sim p_z} [log(1-D(G(z)))]) Dmin−(Ex∼px[logD(x)]+Ez∼pz[log(1−D(G(z)))])
为了训练GAN中的生成器G,我们计算如下损失: 比较生成图像之预测 p i = D ( G ( z i ) ) p_i=D(G(z_i)) pi=D(G(zi))与响应 y i = 1 y_i=1 yi=1。因此,对于GAN生成器,最小化损失函数可以写作如下式4-3.
min G − ( E z ∼ p z [ l o g ( D ( G ( z ) ) ] ) \min \limits_{G} -(\mathbb{E}_{z \sim p_z} [log(D(G(z))]) Gmin−(Ez∼pz[log(D(G(z))])
现在,让我们将之与Wasserstein损失函数对比。
首先,Wasserstein损失要求我们使用 y i = 1 y_i=1 yi=1 和 y i = − 1 y_i=-1 yi=−1 作为标签,而非1和0。我们也将去掉鉴别器最后一层的sigmoid激活函数,使得预测 p i p_i pi不再受限于[0,1],而是可以取 ( − ∞ , ∞ ) (-\infin, \infin) (−∞,∞) 范围内的任何数。因此,WGAN中的鉴别器常被人称作输出一个分数(而非概率)的 评论员 (critic)。
Wasserstein 损失函数定义如下:
− 1 n ∑ i = 1 n ( y i p i ) - \frac{1}{n} \sum \limits_{i=1}^n(y_i p_i) −n1i=1∑n(yipi)
为了训练WGAN评论员D,我们计算如下损失: 比较真实图像之预测 p i = D ( X i ) p_i=D(X_i) pi=D(Xi) 与响应 y i = 1 y_i=1 yi=1,以及比较生成图像之预测 p i = D ( G ( z i ) ) p_i=D(G(z_i)) pi=D(G(zi))与响应 y i = − 1 y_i=-1 yi=−1。因此,对于WGAN评论员,最小化损失函数可以用下式表示:
min D − ( E x ∼ p x [ D ( x ) ] − E z ∼ p z [ D ( G ( z ) ] ) \min \limits_{D} -(\mathbb{E}_{x \sim p_x} [D(x)] - \mathbb{E}_{z \sim p_z} [D(G(z)]) Dmin−(Ex∼px[D(x)]−Ez∼pz[D(G(z)])
换句话说,WGAN评论员试图最大化真实图像和生成图像预测之差。
为了训练WGAN生成器,我计算如下损失: 比较生成图像之预测 p i = D ( G ( z i ) ) p_i=D(G(z_i)) pi=D(G(zi))与响应 y i = 1 y_i=1 yi=1。因此,对于WGAN生成器,最小化损失函数可以写作如下式:
min G − ( E z ∼ p z [ D ( G ( z ) ] ) \min \limits_{G} -(\mathbb{E}_{z \sim p_z} [D(G(z)]) Gmin−(Ez∼pz[D(G(z)])
换句话说,WGAN生成器试图生成图像,且这些生成图像在评论员视角打分越高越好(也即,评论员被糊弄了,以为她们生成的为真)。
Lipschitz限制
现在,我们不再使用sigmoid函数将输出限制在通常的[0,1]范围,而是允许评论员输出 ( − ∞ , ∞ ) (-\infin, \infin) (−∞,∞) 范围内的任何数,这可能让你感到惊讶。因此,Wasserstein损失可能非常大,这通常会令人不安: 在神经网络中我们常常倾向于避免大的数字。
实际上,WGAN的作者指出,为了让Wasserstein损失函数生效,我们还需要在评论员上施加额外的限制。具体的,我们要求评论员是一个 1-Lipschitz 连续函数。让我们把这一点单拎出来,从细节上看看这到底意味着什么。
评论员是一个函数D,将一幅图像转换为一个预测。我们说该函数是 **1-Lipschitz **的,如果它对于任何两张输入图像 x 1 x_1 x1 和 x 2 x_2 x2 ,均能满足下列不等式:
∣ D ( x 1 ) − D ( x 2 ) ∣ ∣ x 1 − x 2 ∣ ≤ 1 \frac{|D(x_1)-D(x_2)|}{|x_1 - x_2|} \leq 1 ∣x1−x2∣∣D(x1)−D(x2)∣≤1
这里, ∣ x 1 − x 2 ∣ |x_1 - x_2| ∣x1−x2∣ 是两张图像的绝对像素差值之平均, ∣ D ( x 1 ) − D ( x 2 ) ∣ |D(x_1)-D(x_2)| ∣D(x1)−D(x2)∣是评论员预测之差的绝对值。本质上,我们对于两张图像之评论员预测变化的速率做了一个限制(例如,梯度之绝对值在各处都近似为1)。我们可以看到,图4-11中的一个 Lipschitz连续一维函数满足要求 — 存在一个双圆锥(白色)其顶点可以沿着曲线平移,使得曲线总是完全在这两个圆锥外 (参考维基百科)。换句话说,在任何点上曲线起伏的速率都有一个限制。
| 小贴士 |
|---|
| 如果你想更深入理解为什么 Wasserstein损失只有在施加此限制方可生效 背后的数学合理性,Jonathan Hui 提供了一个很棒的解释。 |
强制 Lipschitz 限制
在原始的WGAN论文中,作者指出了施加Lipschitz 限制的一种可行方法: 在每批次训练后,将评论员权重修建并限制在一个很小的范围 [ − 0.01 , 0.01 ] [-0.01, 0.01] [−0.01,0.01]。
对这种方法的一个批评意见是:随着我们修剪权重,评论员学习的能力逐渐消失。实际上,即使在原始的WGAN论文中,作者都提到:“在施加Lipschitz限制上,权重裁剪显然是一个糟糕的方法。” 一个强大的评论员对于WGAN是很重要的,因为没有准确的梯度,生成器就无法学会如何调整权重来生成更好的样本。
因此,其他的研究者亦在寻找施加Lipschitz限制并提升WGAN容量以学习复杂特征的替代方法。带梯度惩罚的WGAN就是其中的一种方法。
在介绍这一变种的论文中,作者展示了如果通过损失函数中添加一个梯度惩罚项来施加Lipschitz限制,该项可以在评论员模型之梯度范数偏离1时施加惩罚。这将带来一个稳定的多的训练过程。
在下一章节中,我们将看看如何在我们的评论员中将此额外的项引入损失函数。
梯度惩罚损失
图4-12 是WGAN-GP评论员训练过程的一个框图。如果我们将它与原始的鉴别器训练过程(图4-5)进行比较,我们可以看到关键增加的项目在于Wasserstein损失作为真假图像的损失,并将梯度惩罚项目作为整体损失函数的一部分。

梯度惩罚损失度量 输入图像预测梯度范数 与 1之间的均方差。模型自然会倾向于找到那些使得梯度惩罚项最小化的权重,从而鼓励模型符合Lipschitz限制。
事实上,在训练过程中要计算各处的梯度是不现实的,因此 WGAN-GP 只是对于一些点的梯度进行评估。为了确保均衡的混合,我们使用一组随机的内插图像(连接一批真实图像和一批虚假图像对),如图4-13所示。

在示例4-8中,我们给出了梯度惩罚的计算代码。
def gradient_penalty(self, batch_size, real_images, fake_images):
# batch中的每幅图像得到一个介于0到1之间的随机数,存在向量 alpha中
alpha = tf.random.normal([batch_size, 1, 1, 1], 0.0, 1.0)
diff = fake_images - real_images
# 计算一组内插图
interpolated = real_images + alpha * diff
with tf.GradientTape() as gp_tape:
gp_tap.watch(interpolated)
# 评论员对每幅内插图像打分
pred = self.critic(interpolated, training = True)
# 对于输入图像,计算预测梯度
grads = gp_tape.gradient(pred, [interpolated])[0]
# 计算此向量之L2范数
norm = tf.sqrt(tf.reduce_sum(tf.square(grads), axis=[1,2,3]))
# 函数返回 L2范数和1之间的均方距离
gp = tf.reduce_mean((norm - 1.0) ** 2)
return gp
WGAN-GP之训练
使用Wasserstein损失函数的一个关键优点在于,我们不在需要担心生成器和评论员训练之间的平衡—实际上,当使用Wasserstein损失时,在更新生成器之前,评论员需要训练到收敛,以确保生成器之梯度能够精确更新。这与标准GAN有所不同,在标准GAN中我们不希望鉴别器过分强大。
因此,通过Wasserstein GANs,我们可以在两次生成器更新之间多次训练评论员,以确保其接近收敛。实际应用中一个典型的比例是: 每更新一次生成器,做3-5次评论员更新。
现在,我们引入了Wasserstein-GP背后的两大关键概念 — Wasserstein损失 和 包含在评论员损失函数中的梯度惩罚项。包含了所有这些思想的 WGAN模型训练步骤如下示例4-9所示。
def train_step(self, real_images):
batch_size = tf.shape(real_images)[0]
# 进行评论员更新
for i in range(3):
random_latent_vectors = tf.random.normal(shape=(batch_size, self.latent_dim))
with tf.GradientTape() as tape:
fake_images = self.generator(random_latent_vectors, training = True)
fake_predictions = self.critic(fake_images, training = True)
real_predictions = self.critic(real_images, training = True)
# 计算评论员Wasserstein损失 --- 伪造图像和真实图像的平均预测之差
c_wass_loss = tf.reduce_mean(fake_predictions) - tf.reduce_mean(real_predictions)
# 计算梯度损失惩罚项 (见示例4-8)
c_gp = self.gradient_penalty(batch_size, real_images, fake_images)
# 评论员损失函数是Wasserstein损失和梯度惩罚的加权和
c_loss = c_wass_loss + c_gp * self.gp_weight
c_gradient = tape.gradient(c_loss, self.critic.trainable.variables)
# 更新评论员权重
self.c_optimizer.apply_gradients(zip(c_gradient, self.critic.trainable_variables))
random_latent_vectors = tf.random.normal(shape=(batch_size, self.latent_dim))
with tf.GradientTape() as tape:
fake_images = self.generator(random_latent_vectors, training = True)
fake_predictions = self.critic(fake_images, training = True)
# 计算生成器之Wasserstein损失
g_loss = -tf.reduce_mean(fake_predictions)
gen_gradient = tape.gradient(g_loss, self.generator.trainable_variables)
# 更新生成器之权重
self.g_optimizer.apply_gradients(zip(gen_gradient, self.generator.trainable_variables))
self.c_loss_metric.update_state(c_loss)
self.c_wass_loss_metric.update_state(c_wass_loss)
self.c_gp_metric.update_state(c_gp)
self.g_loss_metric.update_state(g_loss)
return {m.name: m.result() for m in self.metrics}
| WGAN-GP之Batch Normalization |
|---|
| 在训练WGAN-G之前,我们还有一点需要注意: 评论员网络中不要用BN层。这是因为BN层会在相同批次的图像间构建相关性,这会导致梯度惩罚损失有效性缺失。实验结果表明: 即使评论员没有BN层,WGAN-GPs仍然可以产生比较好的结果。 |
目前,我们覆盖了标准GAN和WGAN-GP的几点关键差异,再回顾一下:
- WGAN-GP 使用Wasserstein损失。
- WGAN-GP使用标签1(真实图像),标签-1(伪造图像)。
- 在评论员的最后一层没有sigmoid激活函数。
- 评论员损失函数中包含了一个梯度惩罚项。
- 在每次更新生成器之前,多次训练评论员。
- 评论员网络中没有batch normalization层。
WGAN-GP分析
让我们看看训练25个epochs之后生成器的一些示例输出(图4-14)。

模型学到了脸部的高层次特征,没有明显的模式坍塌出现。
我们也看到了损失函数如何随着时间演化 — 评论员和生成器的损失都高度稳定且收敛。

如果我们比较上一章VAE与WGAN-GP的输出 ,我们可以看到GAN图像普遍更锐利 — 尤其是头发和背景之间的清晰度。这通常是合理的:VAE更倾向于生成模糊彩色边缘的柔和图片,GANs则倾向于生成锐利,更清晰的图片。
另一个事实是,GANs比VAEs更难于训练,一般需要更长的训练时间才能达到满意的质量。但是,目前很多经典的生成式模型都是基于GAN的,因为在GPU上训练大规模GANs的收益是明显的。
条件GAN (CGAN)
截至目前,在本章中,我们已经构建了足以从给定训练集出发生成真实感图像的GANs。但是,我们无法控制想要生成的图像类别 - 例如,一个男人或女人的脸,或者一个大的或小的积木。我们可以从隐空间采样一个随机点,但是对于这个采样点将生成何种图片,我们目前还没有理解的能力。
在本章的最后一部分,我们将注意力转向构建可控生成的GAN — 即所谓的 条件GAN。这一思想首次提出于 Mirza和Osindero等在2014年提出的 “Conditional Generative Adversarial Nets”,它是GAN架构的一个简单扩展。
| 运行示例代码 |
|---|
| 本示例代码可以在Jupyter Notebook的以下路径找到: “notebooks/04_gan/03_cgan/cgan.ipynb”。这部分代码修改自Keras官网上Sayak Paul的杰出CGAN教程。 |
CGAN架构
在本例中,我们将以人脸数据集金发属性为条件来构建CGAN。也即,我们可以显式指出生成的图像是否金发。CelebA数据集提供了这一标签。
高级CGAN架构如图4-16所示。

标准GAN和CGAN的核心差别在于,在CGAN中,我们向生成器和评论员传递了标签相关的额外信息。在生成器中,这个就是简单的以 独热编码向量 插入到隐空间。在评论员中,我们把标签信息作为额外的通道加入到RGB图像。我们通过重复独热编码向量来填充与输入图像相同的形状。
CGANs之所以能够生效,是因为评论员有了关于图像内容的额外信息,因此生成器必须确保其输出图像与给定的标签一致,以此来保持对评论员的糊弄。如果生成器产生了完美的图片,但是与图片标签不一致,那么评论员可以直接判断造假,因为图片和标签不匹配。
| 小贴士 |
|---|
| 在我们的例子中,我们的独热标签长度为2,因为只有两类(金发 或 非金发)。但是,如果你想,你可以有任意多标签 — 例如,你可以在FashionMNIST上训练一个CGAN,通过在生成器中引入长度为10的独热标签向量,并在评论员中引入10个额外的独热编码标签通道,我们可以条件化输出10种不同的衣物类别。 |
在架构上,我们唯一需要做的修改就是将标签信息聚合到生成器和评论员已有的输入中,如下示例4-10所示。
# 图像通道和标签通道分别传入评论员,并连接起来
critic_input = layers.Input(shape=(64,64,3))
label_input = layers.Input(shape=(64,64,2))
x = layers.Concatenate(axis=-1)([critic_input, label_input])
...
# 隐向量和类别标签分别传入生成器,并在Reshape之前连接起来
generator_input = layers.Input(shape=(32,))
label_input = layers.Input(shape=(2,))
x = layers.Concatenate(axis=-1)([generator_input, label_input])
x = layers.Reshape((1,1,34))(x)
CGAN训练
我们还需要在CGAN的train_step上做一些改变,来匹配生成器和评论员的新输入格式,如下样例4-11所示。
def train_step(self, data):
# 从输入数据中将图像和标签解封
real_images, one_hot_labels = data
# 将独热编码向量扩展至与图像相同的尺寸(64x64)
image_one_hot_labels = one_hot_labels[:, None, None,:]
image_one_hot_labels = tf.repeat(image_one_hot_labels, repeats = 64, axis = 1)
image_one_hot_labels = tf.repeat(image_one_hot_labels, repeats = 64, axis = 2)
batch_size = tf.shape(real_images)[0]
for i in range(self.critic_steps):
random_latent_vectors = tf.random.normal(shape=(batch_size, self.latent_dim))
with tf.Gradient() ass tape:
# 生成器喂养了两个输入 --- 随机隐向量 + 独热编码标签向量
fake_images = self.generator([random_latent_vectors, one_hot_labels], training = True)
# 评论员喂养了两个输入 --- 真假图像 + 独热编码标签通道
fake_predictions = self.critic([fake_images, image_one_hot_labels], training = True)
real_predictions = self.critic([real_images, image_one_hot_labels], training = True)
c_wass_loss = tf.reduce_mean(fake_predictions) - tf.reduce_mean(real_predictions)
# 梯度惩罚函数也要求独热标签通道
c_gp = self.gradient_penalty(batch_size, real_images, fake_images, image_one_hot_labels)
c_loss = c_wass_loss + c_gp * self.gp_weight
c_gradient = tape.gradient(c_loss, self.critic.trainable_variables)
self.c_optimizer.apply_gradients(zip(c_gradient, self.critic.trainable_variables))
random_latent_vecotrs = tf.random.normal(shape=(batch_size, self.latent_dim))
with tf.GradientTape() as tape:
# 评论员训练步骤的改变也可以应用于生成器训练步骤
fake_images = self.generator([random_latent_vectors, one_hot_labels], training = True)
fake_predictions = self.critic([fake_images, image_one_hot_labels], training = True)
g_loss = - tf.reduce_mean(fake_predictions)
gen_gradient = tape.gradient(g_loss, self.generator.trainable_variables)
self.g_optimizer.apply_gradients(zip(gen_gradient, self.generator.trainable_variables))
CGAN分析
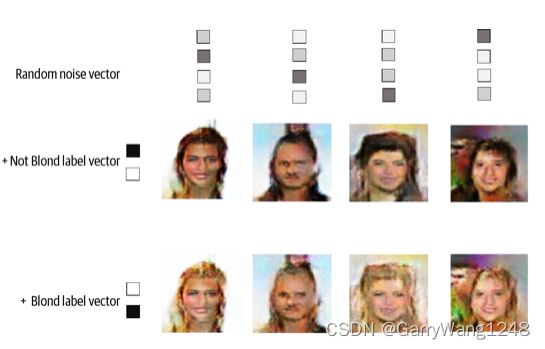
通过输入一个特定的独热向量编码标签,我们可以控制CGAN输出。例如,为了生成非金发人脸,我传入向量[1, 0]。为了生成金发人脸,我们传入向量[0,1]。
图4-17给出了CGAN的输出。这里,我们保持随机隐向量不变,仅仅改变条件类别向量。很显然,CGAN已经将学会了如何利用标签向量来调控头发颜色属性。令我们印象深刻的是,图像的剩余部分并未改变 — 这表明,GAN可以把隐空间中的点按照单个特征解耦合的方式来进行组织。
| 小贴士 |
|---|
| 如果你的数据集中提供了标签,即使你不需要根据label来生成条件化输出,把标签作为GAN输入的一部分通常也是一个好主意,因为它们会提升生成图像的质量。你可以把标签理解为像素输入之外的一个高度信息化的延伸。 |
本章小结
在本章中,我们探索了三种不同的生成对抗网络(GAN): DCGAN, 更复杂的带梯度惩罚的Wasserstein GAN (WGAN-GP), 以及条件GAN (CGAN)。
所有的GANs都是由 生成器 vs 鉴别器 (或评论员) 架构刻画,其中鉴别器努力区分真实和伪造图像,生成器致力于糊弄鉴别器。通过在这两个相反的训练过程中做均衡,GAN的生成器渐渐会学到如何生成与训练集中样本相似的观察。
首先,我们观察了怎么训练DCGAN来产生玩具积木图形。网络可以学会如何真实的用图像表示3D物体,包括精确表示阴影,形状,纹理等。我们也探索了GAN训练失败的多种原因,包括模式坍塌以及梯度消失。
接下来,我们探索了Wasserstein损失函数如何修复GAN中的大部分问题,并使得GAN的训练过程更稳定。WGAN-GP 在训练过程中通过在损失函数中引入一个梯度范数限制项(强制范数接近1)强制了 1-Lipschitz 要求。
我们应用WGAN-GP到人脸生成问题,并看到了我们如何从标准正态分布采样点,并进而生成新的人脸。这个采样过程很接近VAE,尽管GAN生成的人脸大有不同 — 通常更锐利。
最后,我们构建了CGAN,这允许我们控制图像产生的类别。这是因为,通过传入标签作为生成器和评论员的输入,给了网络所需的额外信息来根据给定标签产生条件化输出。
总之,我们已经看到了GAN框架多么灵活,并且能够应用于多个有趣的问题域。特别的,GANs已经驱动了图像生成领域的重要发展,如我们将在第10章中看到的。
在下一章,我们将探索一个不同的生成式模型家族—自回归模型,它特别适合于对序列数据建模。
译者的话: 在 diffusion 模型近乎一统天下的今天,仍然有诸多研究者基于GANs提出了许多创新性工作(如dragGAN等),在一些场景下取得了比扩散模型更好的效果。对于致力于生成式人工智能研究的朋友来说,GAN相关的技术进展仍需要保持关注。后期,我也将添加一些关于GANs的相关工作介绍。


