组合总数_

题目描述

来源：leetcode_hot100_39
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。
对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：
输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：
输入: candidates = [2], target = 1
输出: []

提示：
1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素 互不相同
1 <= target <= 40

错误示范
思路：见正解

class Solution {
public:
    vector<vector<int>> ans;
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        if(candidates.size()==0){
            return ans;
        }
        sort(candidates.begin(),candidates.end());
        vector<int> path;
        dfs(candidates,target,0,path);
        return ans;
    }

    void dfs(vector<int>& candidates, int tar,int begin,vector<int> path){
        if(tar==0){
            ans.push_back(path);
            return ;
        }
        
        for(int i=begin;i<candidates.size();i++){
            if(candidates[i]<=tar){
                path.push_back(candidates[i]);
                dfs(candidates,tar-candidates[i],i,path);
            }else{
                path.pop_back();//这里错了
                return ;
            }
        }
    }
};

错误原因：函数传递形参等到函数结束后是会恢复的，深一层函数里的path操作并不会影响上一层的path。

//答案错误
输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,2,3],[2,3,6,7]]

正解

思路：想到了建树然后从根节点到子节点的每条路径都是一个解，但没想到怎么去重，看了解析才明白。
刚好符合递归问题

• 子问题可分解为target-candidates[i]
• 边界条件是target==0

利用回溯算法+剪枝
普通回溯：

有剪枝（去重）功能的回溯：

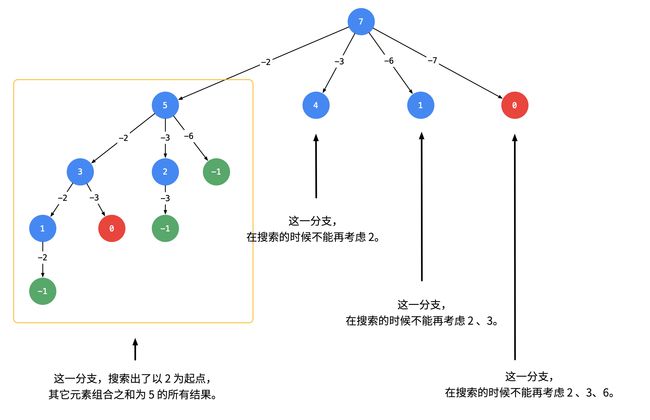
从每一层的第 2 个结点开始，都不能再搜索产生同一层结点已经使用过的 candidate 里的元素。

class Solution {
public:
    vector<vector<int>> ans;
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        if(candidates.size()==0){
            return ans;
        }
        sort(candidates.begin(),candidates.end());//从小到大排序
        vector<int> path;
        dfs(candidates,target,0,path);
        return ans;
    }

    void dfs(vector<int>& candidates, int tar,int begin,vector<int> path){
        if(tar==0){
        //如果恰好是0了，证明该解成立，加入path，不是0还要另看是没递归到底还是不是解
            ans.push_back(path);
            return ;
        }
        
        for(int i=begin;i<candidates.size();i++){//begin就是为了剪枝去重
            if(candidates[i]<=tar){//candidates[i]<=tar证明还没递归到底
                path.push_back(candidates[i]);//当前值放入当前解path中
                dfs(candidates,tar-candidates[i],i,path);//tar-candidates[i]作为目标进行下一层递归
                path.pop_back();//如果刚好合适的话（是解）是走不到这里的，到dfs函数一开始就被if(tar==0)截断return了，所以能走到这里的都不是解
            }else{
                return ;//如果tar已经小于candidates[i]，那他已经小于candidates数组i及以后最小的数了（毕竟sort过，是升序排列），所以可以不用再遍历，直接return
            }
        }
    }
};