基本路径测试
基本路径
基本路径(线性无关回路):两个环路线性无关,当且仅当经过的边有差异,我有一条边你没有,你有一条边我没有。即任何一个环路,都应该拥有一个边是其他环路没有的。
用基本路径覆盖法设计下列程序段的测试用例。
画控制流图
- 开始结点不含语句,就是单纯一个标识结点;
- While或if里面有多个and,or连接的条件要分成独立的结点;
- Return语句就是结束结点;
- For循环第一个赋值要单独一个结点,判断也要一个结点
例1
int insert(int a[],int b,int n)
{ int i;
if(n==0) a[0]=b;
else
{
i=n-1;
while((i>=0)&&(a[i]>b))
{
a[i+1]=a[i];
i--;
}
a[i+1]=b;
}
n++;
return n;
}
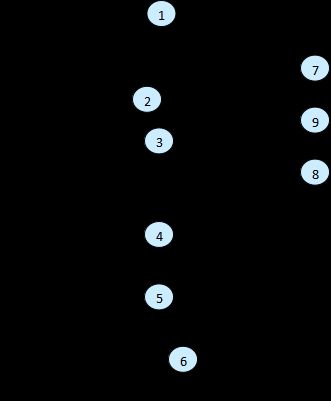
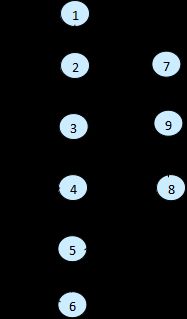
环形复杂度为:3+1=4或11-9+2=4
基本路径:
(1)1-2-7-9
(2)1-2-3-4-8-9
(3)1-2-3-4-5-8-9
(4)1-2-3-4-5-6-4-8-9
测试用例:
(1)输入:n=0,b=1;预期输出:a:{1}
(2)无
(3)输入:n=1,a:{1},b=2;预期输出:a:{1,2},n=2
(4)输入:n=1,a:{2},b=1;预期输出:a:{1,2},n=2
例2
int del(int a[],int b,int n)
{
int i=0,j;
while((i<n)&&(a[i]!=b)) i++;
if(i>=n) cout<<"not this element";
else
{
for(j=i;j<n-1;j++)
a[j]=a[j+1];
n--;
}
return n;
}
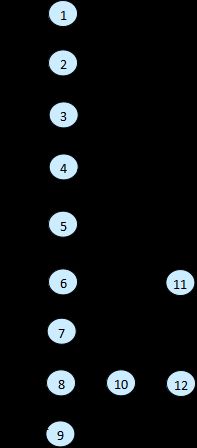
环形复杂度为:4+1=5或15-12+2=5
基本路径:
(1)1-2-3-6-11-12
(2)1-2-3-4-6-11-12
(3)1-2-3-4-5-3-6-11-12
(4)1-2-3-4-6-7-8-9-8-10-12
(5)1-2-3-4-5-6-7-8-10-12
测试用例:
(1)输入:n=0,b=1;预期输出:n=0,not this element
(2)输入:无
(3)输入:n=1,a={1},b=2;预期输出:n=1,not this element
(4)输入:n=1,a={1},b=1;预期输出:n=0
(5)输入:n=2,a={1, 2},b=2;预期输出:n=1
例3
//求矩阵中的最大值,m和n传递数组的行数和列数
int max_element(int a[ ][4], int m, int n, int &row, int &colum)
{ int i, j, max;
max=a[0][0]; row=0; colum=0;
for (i=0; i<m; i++)
for (j=0; j<n; j++)
if (a[i][j]>max)
{ max=a[i][j]; row=i; colum=j; }
return max;
}

V(G)=12-10+2=4(或V(G)=B+1=3+1=4)
基本路径:
(1)1-2-3-4-11
(2)1-2-3-4-5―6-7-8-9-6-10-4-11
(3)1-2-3-4-5-6-10-4-11
(4)1-2-3-4-5-6-7―9-6-10-4-11
测试用例:
(1)m=0, n=0, 数组元素:没有
(2)m=1, n=1, 数组元素:1 ,预期输出 1
(3)m=1, n=0, 数组元素:没有
(4)m=1, n=2, 数组元素:1 2 预期输出2
例4
void count(char s[],int &caps,int &low)
{ caps=low =0;
for(int i=0;s[i] !='\0';i++)
if(s[i]>='A'&&s[i]<='Z') caps++;
else if(s[i]>='a'&&s[i]<='z') low++;
}
注:字符0的ASCII码为48,字符A的ASCII码为65,字符[的ASCII码为91,字符a的ASCII码为97,字符{的ASCII码为123。

环形复杂度15-11+2=6或5+1=6
基本路径:
(1)1-2-3-11
(2)1-2-3-4-7-10-3-11
(3)1-2-3-4-5-6-10-3-11
(4)1-2-3-4-5-7-10-3-11
(5)1-2-3-4-5-7-8-10-3-11
(6)1-2-3-4-5-7-8-9-10-3-11
测试用例:
(1)输入:s为" "(空串);预期输出:caps=0,low =0
(2)输入:s为"1 ";预期输出:caps=0,low =0
(3)输入:s为"A “;预期输出:caps=1,low =0
(4)输入:s为”[ “;预期输出:caps=0,low =0
(5)输入:s为”{ “;预期输出:caps=0,low =0
(6)输入:s为"a”;预期输出:caps=0,low =1
找基本路径算法
- 起点和终点随便找一条路;
- 哪个结点是判定结点,有多个判定结点随便选一个;
- 将其翻转(原来走真分支,现在走假分支);
- 只要有一条原来没有的边,就得到一条新的基本路径。
拿例2说:
- 先找出1-2-3-6-11-12,3和6都是判定结点,先走3的另一个分支,得到1-2-3-4-6-11-12。注意,每一个判定条件,一旦在上面生成新的路径之后,真分支假分支就已全部覆盖,换句话说,它已经没有边生成新的基本环路了。这个时候3就完全发掘完毕。再看4和6.
- 选4,走另一个分支,得到1-2-3-4-5-3-6-11-12
- 4发掘完毕,看6,选择6的另一个分支,后面有个判定结点8,随便选一个分支,得到1-2-3-4-6-7-8-10-12;
- 再看8的另一个分支,得到1-2-3-4-6-7-8-9-8-10-12
注意:转圈的情况,8-9-8,其中8-9和9-8是两个不同的边。
总结:就是遍历每个判定结点的两个分支,都要走一遍。此外找好基本路径后检查一些两两是否线性无关。