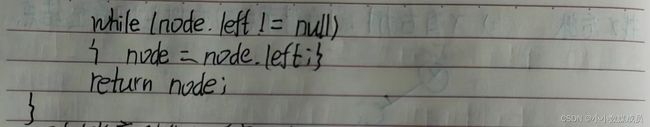二叉树算法
每日一句:少年就是少年,他们看春风不喜,看夏蝉不烦,看秋风不悲,看冬雪不叹,看满身富贵懒察觉,看不公不允敢面对。只因他们是少年!
目录
用递归和非递归两种方式实现二叉树的先序、中序、后序遍历
递归方法:
非递归方法:
如何完成二叉树的宽度优先遍历(常见题目:求一棵二叉树的宽度)
二叉树的相关概念及其实现判断
1.如何判断一棵二叉树是否是搜索二叉树?
2.如何判断一棵二叉树是完全二叉树?
3.如何判断一棵二叉树是否是满二叉树?
二叉递归套路:
判断满二叉树,用递归套路
给定两个二叉树的节点node1和node2,找到他们的最低公共祖先节点
在二叉树中找到一个节点的后继节点
【题目】现有一种新的二叉树节点类型如下:
Public class Node
{
public int Value;
Public Node left;
Public Node right;
Public Node parent;
Public Node(int val)
{value=val;}}
该结构比普通二叉树节点结构多了一个指向父节点的parent指针
假设有一棵Node类型的节点组成的二叉树,树中每个节点的parent指针都正确地指向自己的父节点,头节点的parent指向null
只给一个在二叉树中的某个节点Node,请实现返回node的后继节点的函数
二叉树的序列化和反序列化
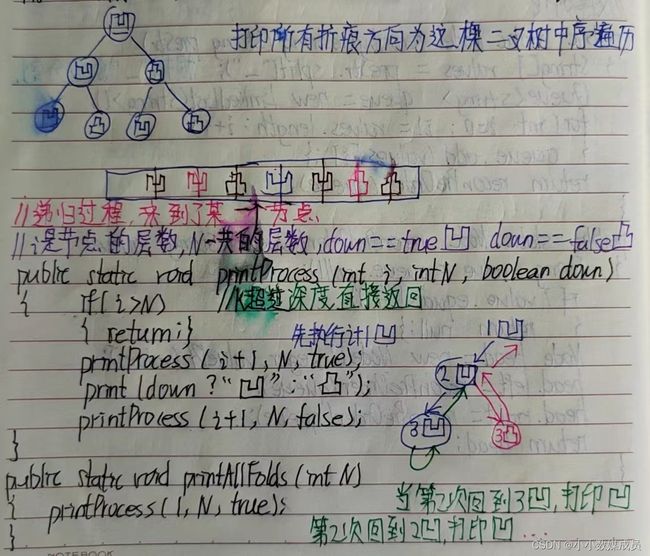
折纸问题
请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开
此时折痕是凹下去的,即折痕突起的方向指向纸条的背面,如果从纸条的下边向上方连续对折2次,压出折痕后展开,此时有三条折痕,从上到下依次是下折痕,下折痕和上折痕
给定一个输入参数N,代表纸条都从下边向上方连续对折N次
请从上到下打印所有折痕的方向
例:N=1时,打印:down;N=2时,打印:down down up
二叉树
二叉树节点结构
Class Node
{V value;
Node left;
Node right;
}
用递归和非递归两种方式实现二叉树的先序、中序、后序遍历
递归方法:
先序:
递归序加工过来,第一次来到一个节点时,打印,二、三两次来到的时候什么也不干
中序:
递归序加工过来,第二次来到一个节点时,打印,一、三两次来到的时候什么也不干
后序:
递归序加工过来,第三次来到一个节点时,打印,二、一两次来到的时候什么也不干
代码:
非递归方法:
先序:
把头节点放到栈里
从栈中弹出一个节点cur—>打印cur—>先右再左(如果有)—>周而复始
后序:
从栈中弹出一个节点cur—>cur放入收集栈—>先左再右—>周而复始
中序:
每棵子树,整棵树左边界进栈—>依次弹的过程中,打印—>对弹出节点右树,周而复始
代码:
如何完成二叉树的宽度优先遍历(常见题目:求一棵二叉树的宽度)
二叉树的深度优先遍历为先序遍历
宽度遍历用队列,头部进、尾部出,先进先出
先把头节点放队列里,每次弹出就打印,先放左、再放右,周而复始
二叉树的相关概念及其实现判断
1.如何判断一棵二叉树是否是搜索二叉树?
【搜索二叉树】:对于每一棵子树来说,左树节点都比它小,右树节点都比它大
2.如何判断一棵二叉树是完全二叉树?
【完全二叉树】:最后一层满或从左到右依次变满
判断方式:二叉树按宽度来遍历
依次遇到每个节点过程中,出现情况:
1) 遇到任何一个节点,如果有右孩子,没左孩子,直接返回false
2)在1)成立条件下,如果第一个左、右两孩子不双全,后续遇到所有皆为叶节点,否则false
3.如何判断一棵二叉树是否是满二叉树?
方法一:先求树的最大深度l,再统计树的节点个数N。满足N=2l![]() -1,则为满二叉树
-1,则为满二叉树
二叉递归套路:
判断是否为搜索二叉树,用递归套路——从左树要信息,从右树要信息,罗列可能性
递归套路可以解决一切树型DP问题
基于可以向左树要信息,右树要信息,罗列可能性,做全集搞递归结构,固定代码结构
判断满二叉树,用递归套路
递归套路返回两个值:整棵树高度、节点个数
给定两个二叉树的节点node1和node2,找到他们的最低公共祖先节点
方法一:
查D、F的最低公共祖先节点
先把D、B、A放到一个set里,让F往上走,F不在set里,E也不在,B在,所以B为D、F的最低公共祖先
方法二:
两种情况:
- O1为O2的最低公共祖先或O2为O1的最低公共祖先
- O1、O2彼此不互为最低公共祖先
如果一个树既没有O1,也没有O2,返回null
A向右树要答案,返回null
A向左树要答案看B,B看D,D看左树得O1,D看右树得null
所以B左侧返回值O1,B右侧返回值O2,B返回自己
在二叉树中找到一个节点的后继节点
【题目】现有一种新的二叉树节点类型如下:
Public class Node
{
public int Value;
Public Node left;
Public Node right;
Public Node parent;
Public Node(int val)
{value=val;}
}
该结构比普通二叉树节点结构多了一个指向父节点的parent指针
假设有一棵Node类型的节点组成的二叉树,树中每个节点的parent指针都正确地指向自己的父节点,头节点的parent指向null
只给一个在二叉树中的某个节点Node,请实现返回node的后继节点的函数
方法一:
在二叉树的中序遍历的序列中,node的下一个节点叫作node的后继节点
后继节点就是中序遍历中,一个节点的下一个节点
代价高,要求遍历所有的节点,得到一个List,才能知道任何一个节点的后继,复杂度O(N)
方法二:
找x后继
- x有右树,则后继节点为右树上的最左节点
- x无右树,看往上走是不是父的左孩子,不是接着往上走,是的话,父为x的后继
二叉树的序列化和反序列化
就是内存里的一棵树如何变成字符串形式,又如何从字符串形式变成内存里的树
折纸问题
请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开
此时折痕是凹下去的,即折痕突起的方向指向纸条的背面,如果从纸条的下边向上方连续对折2次,压出折痕后展开,此时有三条折痕,从上到下依次是下折痕,下折痕和上折痕
给定一个输入参数N,代表纸条都从下边向上方连续对折N次
请从上到下打印所有折痕的方向
例:N=1时,打印:down;N=2时,打印:down down up
打印所有折痕方向为这棵二叉树中序遍历