深度学习中的不确定性

原文参考这里，深度学习中的两种不确定性

注: 本文中，概念、公式与实验均基于 Alex Kendall & Yarin Gal的论文:https://arxiv.org/pdf/1703.04977.pdf

不确定性（Uncertainty）

目前深度学习在很多领域的表现都非常好，像是无人驾驶使用的语义分割上的准确率相当惊人。但是众所周知，Tesla无人驾驶一段时间前发生了很多起事故。其中导致一人死亡。最终原因是算法误将一辆浅色卡车误判为天空。

这个事故暴露出的一个问题便是，现在我们传统深度学习算法几乎只能给出一个特定的结果，而不能给出模型自己对结果有多么confident. 的确，在分类问题中，我们会在网络的最后一层添加一个softmax函数来获得概率，但是试想下边这样一个情况：假如我训练了一个分类人脸和猩猩脸的模型。但是我在test阶段给了模型一个大脸猫的图片，我们的模型很会给出一个相当不准确的结果，而没有办法告诉我们“我真不知道这是个什么鬼。” 可能有人说，在这种情况下，最终结果会不会输出一个[0.5,0.5]的结果，来表示自己对结果不确定呢？其实，softmax函数的特性决定了这种情况下网络不太可能输出[0.5,0.5]这样的结果[1]。

这个问题是一个很重要的问题，我曾经在知乎看到过一个搞航天器的朋友回答，为什么ML现在在航空航天领域没有办法应用，他的回答说NN可以在多数情况下给出一个特别特别好的结果，但是偶尔会给出一个特别糟糕的结果，然而这个特别糟糕的结果在他们这个领域是绝对无法被接受的。如果模型可以在输出这个结果的同时，给出一个非常低的置信度，人类就可以被告知需要介入了，那么ML就可以在更广泛的领域进行应用。

那么如何让网络获得一个置信度的输出呢？目前一个非常普遍的方法是利用BNN (Bayesian Neural Network)。BNN的原理大体上是，我们网络中每个参数的weight将不再是一个特定的数字，取而代之的是一个先验分布。这样我们train出来的网络将不再是一个函数，而是一个函数的分布[2]。通过这个分布，我们便可以得到一个对结果的置信度。但是，实现过BNN和使用过pyro的朋友们应该知道，BNN是比较难应用在动辄上百卷积层的大型网络上的。它的训练速度，计算复杂度，都限制了它的发展。

本文将讨论深度学习中不同原因导致的不确定性，并介绍如何量化这些不确定性。我们将通过一种名为MC Dropout (Monte Carlo Dropout)的方法来进行贝叶斯推断，之后对loss function的修改来得到不确定性。

偶然不确定性和认知不确定性（Aleatoric Uncertainty & Epistemic Uncertainty）

我们先来解释深度学习中存在的两种种类不同的不确定性。

1. 偶然不确定性

我们初高中学物理的时候，老师肯定提过偶然误差这个词。我们做小车下落测量重力加速度常数的时候，每次获得的值都会有一个上下起伏。这是我们因为气流扰动，测量精度不够等原因所造成的，是无法被避免的一类误差。在深度学习中，我们把这种误差叫做偶然不确定性。

从深度学习的角度来举例子，我们举一个大家应该很比较熟悉的人脸关键点回归问题[3]:

我们可以看到，对于很相似的一组数据，dataset的标注出现了比较大的误差（见右图的右侧边缘）。这样的误差并不是我们模型带入的，而是数据本来就存在误差。数据集里这样的bias越大，我们的偶然不确定性就应该越大。

2.认知不确定性

认知不确定性是我们模型中存在的不确定性。就拿我们文章一开始举的例子来说，假设我们训练一个分类人脸和猩猩脸的模型，训练中没有做任何的增强，也就是说没有做数据集的旋转，模糊等操作。如果我给模型一个正常的人脸，或者是正常猩猩的脸，我们的模型应该对他所产生的结果的置信度很高。但是如果我给他猫的照片，一个模糊处理过得人脸，或者旋转90°的猩猩脸，模型的置信度应该会特别低。换句话说，认知不确定性测量的，是我们的input data是否存在于已经见过的数据的分布之中。

两种不确定性的量化

注：本文只关注对回归问题不确定性的量化。对于分类问题，我下方列出的公式会变得更为复杂，我将会在 《深度学习中的两种不确定性（下）》中详细叙述。

1. 认知不确定性的量化

和我们以往所做的不同，本文为了获得认知不确定性，将不会在测试阶段禁用Dropout。

这是为什么呢？我们还是需要从BNN说起。

BNN归根结底的原理，是想求一个后验分布 P(W|D)P(W|D) ,其中 WW 为权重， DD 为数据集。如果利用贝叶斯公式，我们将会得到如下公式：

P(W|D)=P(D|W)P(W)P(D)P(W|D)=\frac{P(D|W)P(W)}{P(D)}\\

其中，想得到 P(D)P(D) 这一项是非常困难的，首先，这个 P(D)P(D) 所代表的其实就是真实数据分布，理论上根本获得不了（如果能轻易获得的话，还要ML干什么…）。其次，你可能会想到这个公式:

P(D)=∑iP(D|Wi)P(Wi)P(D)=\sum_iP(D|W_i)P(W_i)\\

这个公示的意思是，你需要遍历所有 WW 来计算 P(D)P(D) ，但是这个是显然行不通的。

现在我们就要想办法解决后验不好算的问题，贝叶斯神经网络一般是用variational inference来算的，感兴趣的读者可以在我的参考阅读里找到更多信息。我们所要用的是另外一种方法，名为蒙特卡洛方法(Monte Carlo method)。

蒙特卡洛方法的本质就是通过有限次的sample，来对我们的这个后验分布 P(W|D)P(W|D) 产生一个估计，然后我们就可以用获得的这个近似分布来当作 P(W|D)P(W|D) 用，而有了这个后验分布，我们就可以知道 DD 到底在不在我们已经学习的分布中，从而获得认知不确定性。

但是，我们的网络每次喂它一次数据，他出来的肯定是一个固定的值啊，每次sample的结果都一样没有办法用蒙特卡洛方法呀？这就是为什么我们选择在testing阶段也不禁用Dropout，把Dropout当作一个天然的随机发生器，这样我们不需要对我们的现有网络做任何改动，就可以获得 P(W|D)P(W|D) 。对推导过程感兴趣的小伙伴可以在参考阅读[4]中找到非常详尽的推导过程。

所以归根结底，如何获得认知不确定性呢？虽然上边的原理非常的晦涩，但实际上，这个操作非常的简单，你只需要把数据喂进网络 TT 次，然后把得到的结果取一个平均值，就是你的最终预测，把结果算一个方差，结果就是你的认知不确定性，公式如下所示：

E(y)=1T∑txtVar(y)=σ2+1T∑tf(xt)Tf(xt)−E(y)TE(y)E(\boldsymbol y)=\frac{1}{T}\sum_tx_t\\ Var(\boldsymbol y)=\sigma^{2+\frac{1}{T}\sum_tf(x_t)}Tf(x_t)-E(\boldsymbol y)^TE(\boldsymbol y)

其中这个 Var(y)Var(\boldsymbol y) 就是你的认知不确定性。至于这个 σ2\sigma^2 是哪来的，我们在接下来讲。

2. 偶然不确定性的量化

对于偶然不确定性，作者用非常复杂的方式（并没有在论文中说明，但是在参考文献中有，有兴趣的读者可以阅读一下）推出了损失函数:

L(θ)=1N∑i=1N||yi−f(xi)||22σ(xi)2+12log⁡(σ(xi)2)L(\theta)=\frac{1}{N}\sum_{i=1}^{{N}\frac{||y_i-f(x_i)||}2}{2\sigma(x_i)^{2}+\frac{1}{2}\log(\sigma(x_i)}2)\\

我们现在的模型表示为 ff ，模型对应的输出为 {f(xi),σ2}\{f(x_i),\sigma^2\} 。损失函数中，这个 σ(xi)2\sigma(x_i)^2 是描述模型在数据 xix_i 上的偶然不确定性，也就是数据所自带的方差。我们的模型现在将通过无监督学习来学习这个方差。这个损失函数的推导很复杂，不过我们可以直观、定性地理解这个损失函数。

我们设想一个非常简单的回归问题，training set是一个sin函数加上一个noise（下边的简单实验就是用的这个数据集），我们训练的目的是去尽可能的拟合这个带噪声的sin，从而希望让我们的模型去接近真实的数据分布sin。假设网络没有regularization，overfitting了，那么对于每个 xix_i ， ||yi−f(xi)||2||y_i-f(x_i)||^2 将都会等于0。但是我们现在网络是有regularization在里边的(Dropout)，所以我们的网络会去尽可能地拟合一个趋势，而不是把每个数据点全部硬记住。那么现在我们就可以把误差 ||yi−f(xi)||2||y_i-f(x_i)||^2 去当作一个数据本身带的误差。换句话说，假如我带正则化的网络已经在带噪声的sin上train的很好，已经学会了趋势，但是始终有一个很小的误差，那么这个误差就可以被当作那个noise了。这个损失函数通过把 ||yi−f(xi)||2||y_i-f(x_i)||^2 除以 σ(xi)2\sigma(x_i)^2 ,来尝试把这个noise造成的损失抵消掉。那为什么要加入后边 12log(σ(xi)2)\frac{1}{2}log(\sigma(x_i)^2) 这个类似于正则项的东西呢？因为如果只去除 σ(xi)2\sigma(x_i)^2 ，网络会倾向把所有 σ2\sigma^2 都预测成无穷大，来最小化损失函数。加上这个 12log(σ(xi)2)\frac{1}{2}log(\sigma(x_i)^2) ，我们的网络将学着只在 ||yi−f(xi)||2||y_i-f(x_i)||^2 非常大的时候，才去调高 σ(xi)2\sigma(x_i)^2 的值。通过这样的方式，我们的网络就学会了如何输出偶然不确定性。原论文作者说，这样的结构并不是故意设计的，而是推导出的性质。

这样，每给定一个数据 xx ，模型就可以输出一个结果，和一个代表偶然不确定性的 σ2\sigma^2 ，同时，我们这个 σ2\sigma^2 也会用到认知不确定性的计算里。

但是实际训练中，我们将不让网络直接输出 σ2\sigma^2 ,因为如果 σ2\sigma^2 是0，我们的损失函数会直接nan。所以我们训练时，让网络输出 log(σ2)log(\sigma^2) ，来防止0的出现。同时，我们的损失函数会变为：

L(θ)=1N∑i=1N12exp⁡(−log⁡(σ2))||yi−f(xi)||2+12log⁡(σ(xi)2)L(\theta)=\frac{1}{N}\sum_{i=1}^{N} \frac{1}{2} \exp(-\log(\sigma^2)) ||y_i-f(x_i)||^{2+\frac{1}{2}\log(\sigma(x_i)}2)\\

应用上来说，如果想选一个threshold的值，尝试reject掉不确定的结果的话，可以把两个不确定性加起来用。

实验

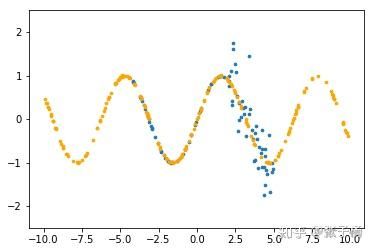
我们首先在一个非常简单的数据集上做一下实验。这是一个简单的sin函数，蓝色数据是我们的训练数据，橙色数据是我们的测试数据。

其中,在区间[2.5,5.0]内，我们对训练数据施加了一个服从分布 N(0,σ2=0.5)\mathcal N(0,\sigma^2=0.5) 的噪声。注意，测试数据的范围明显超过了训练数据。我们使用Adam，lr=0.001，weight_decay=1e-4, Dropout概率为0.1来进行训练，最终获得了如下结果:

偶然不确定性:

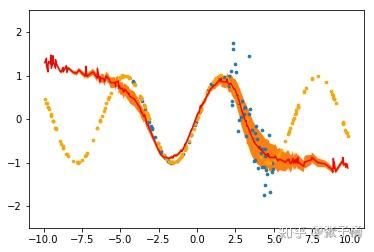
红线为预测，橙色面积为1x偶然不确定性

认知不确定性:

红线为预测，橙色面积为1x认知不确定性

我们可以看到，偶然不确定性在加过噪声的区间明显上升。而认知不确定性在training set范围之外逐渐上升。

接下来，我们用Alex Kendall & Yarin Gal论文里的例子来看看这个方法在更复杂的问题上的表现，以下图片均来自本文一开始提到的论文（本来我是想自己跑一个用自己的结果的，但是手头没显卡。。）。

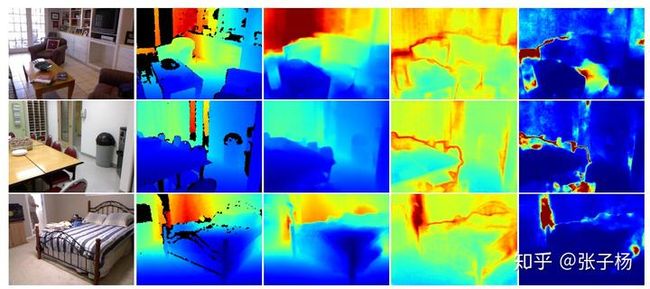
作者们用DenseNet，在NYUv2 depth上跑了一个深度回归，下边是结果

从左到右: 输入图片，ground truth，网络输出，偶然不确定性，认知不确定性

我们可看到，偶然不确定性很高的地方往往是那些过于深，没有标注深度信息的地方。认知不确定性主要集中在物品边缘，以及深度很深这些网络非常容易预测失败的地方。详细信息可以参考论文。

写在最后

我们介绍了如何使用MC dropout来确定网络中的不确定性，但是本文只限于讨论了比较简单的回归问题。至于分类问题，公式会变得比较复杂，我现在在跑一个DenseNet的语义分割模型，跑完后整理好，我会在【实验笔记】深度学习中的两种不确定性（下）中详述。

感谢阅读！

参考阅读

[1] [0.5,0.5]这样的结果在softmax中不太好出现的原因请参考: http://www.cs.ox.ac.uk/people/yarin.gal/website/blog_3d801aa532c1ce.html

[2] BNN的详细原理可以参考：https://towardsdatascience.com/making-your-neural-network-say-i-dont-know-bayesian-nns-using-pyro-and-pytorch-b1c24e6ab8cd

[3] 样例数据集以及参考数据来自：Exploring YouTube Faces with Keypoints Dataset

[4] http://www.cs.ox.ac.uk/people/yarin.gal/website/thesis/thesis.pdf