希尔排序及其优化方案

希尔排序

1. 基本思路
2. 运行轨迹
3. 代码实现
4. 性能分析
5. 优化方案

---

1、基本思路

什么希尔排序？ 一种基于插入排序的快速的排序算法。

希尔排序为了加快速度简单的改进了插入排序，交换不相邻的元素 以对数组的局部进行排序，并最终用插入排序将局部有序的数组排序。（局部有序的数组很适合插入排序）

希尔排序的思想？ 使数组中任意间隔为 h 的元素都是有序的。这样的数组被称为 h 有序数组，也就是说：一个 h 有序数组就是 h 个相互独立的有序数组编织在一起组成的一个数组。

它的一种实现方法： 在插入排序的代码中将移动元素的距离由 1 改为 h 即可。

h 的取值？ while( h < arr.length/3 ) h = 3*h + 1 ； //（1、4、13、40、121、364、1093…）

优点：希尔排序对于中等大小的数组，运行时间是可以接受的，代码量少，且不需要使用额外的内存空间。

---

2、运行轨迹

增幅 h 的初始值是数组长度乘以一个常数因子，最小为 1 。
当 h = 4 时，4-sort；
当 h = 1 时，1-sort；

---

3、代码实现

根据排序算法类的模板实现选择排序（提醒：点蓝字查看详情）

import java.util.Random;

/**
 * 希尔排序
 *
 * @author TinyDolphin
 *         2017/5/30 22:33.
 */
public class Shell {
    /**
     * 排序实现
     *
     * @param arr 待排序数组
     */
    public static void sort(Comparable[] arr) {
        int length = arr.length;
        int h = 1;
        while (h < length / 3) {
            h = 3 * h + 1;  // 1 , 4 , 13 , 40 , 121 , 364 , 1093...
        }
        while (h >= 1) {
            // 将数组变为 h 有序
            for (int indexI = h; indexI < length; indexI++) {
                for (int indexJ = indexI; indexJ >= h && less(arr[indexJ], arr[indexJ - h]); indexJ -= h) {
                    exch(arr, indexJ, indexJ - h);
                }
            }
            h = h / 3;
        }
    }

    /**
     * 比较两个元素的大小
     *
     * @param comparableA 待比较元素A
     * @param comparableB 待比较元素B
     * @return 若 A < B,返回 true,否则返回 false
     */
    private static boolean less(Comparable comparableA, Comparable comparableB) {
        return comparableA.compareTo(comparableB) < 0;
    }

    /**
     * 将两个元素交换位置
     *
     * @param arr    待交换元素所在的数组
     * @param indexI 第一个元素索引
     * @param indexJ 第二个元素索引
     */
    private static void exch(Comparable[] arr, int indexI, int indexJ) {
        Comparable temp = arr[indexI];
        arr[indexI] = arr[indexJ];
        arr[indexJ] = temp;
    }

    /**
     * 打印数组的内容
     *
     * @param arr 待打印的数组
     */
    private static void show(Comparable[] arr) {
        for (int index = 0; index < arr.length; index++) {
            System.out.print(arr[index] + " ");
        }
        System.out.println();
    }

    /**
     * 判断数组是否有序
     *
     * @param arr 待判断数组
     * @return 若数组有序，返回 true，否则返回 false
     */
    public static boolean isSort(Comparable[] arr) {
        for (int index = 1; index < arr.length; index++) {
            if (less(arr[index], arr[index - 1])) {
                return false;
            }
        }
        return true;
    }

    public static void main(String[] args) {
        Integer[] arr = new Integer[100000];
        for (int index = 0; index < 100000; index++) {
            arr[index] = new Random().nextInt(100000) + 1;
        }
        long start = System.currentTimeMillis();
        sort(arr);      //耗费时间：480ms
        long end = System.currentTimeMillis();
        System.out.println("耗费时间：" + (end - start) + "ms");
        assert isSort(arr);
    }
}

---

4、性能分析

算法的性能不仅取决于 h ， 还取决于 h 之间的数学性质，比如它们的公因子等。

使用递增序列 1、4、13、40、121、364… 的希尔排序所需的比较次数不会超过 N 的若干倍乘以递增序列的长度。

在实际应用中，h 的取值使用以上递增序列基本就足够了。但是我们为了追求性能的提升，也使用以下的序列，使性能提高 20%-40% 。1、5、19、41、109、209、505、929、2161、3905、8929、16001、36289、64769、146305、260609（这是通过 9×4^k-9×2^k+1(k=1,2,3,4,5…) 和 4^k-3×2^k+1(k=2,3,4,5,6…) 综合得到的）

希尔排序更加高效的原因：它权衡了子数组的规模和有序性。

和选择排序以及插入排序形成对比的是：希尔排序也可以用于大型数组。它对任意排序（不一定是随机的）的数组表现也很好。希尔排序比插入排序和选择排序要快的多，并且数组越大，优势越大。【提示：点击蓝色字体，可以查看其详细信息。】

什么时候用希尔排序？ 当你需要解决一个排序问题而又没有系统排序函数可用（例如直接接触硬件或是运行于嵌入式系统中的代码）时，可用先用希尔排序，然后再考虑是否值得将它替换为更加复杂的排序算法。

※ 研究算法的设计和性能的主要原因之一：通过提升速度来解决其他方式无法解决的问题。

---

5、优化方案

第一种：使用更为复杂的递增序列，性能可以提高 20%-40%（这里就不说了，上述的递增序列够用）

第二种：因为是基于插入排序的，所以可以使用其插入排序中给出的优化方案。

优化之后运行轨迹：
增幅 h 的初始值是数组长度乘以一个常数因子，最小为 1 。
当 h = 4 时，4-sort；
当 h = 1 时，1-sort；

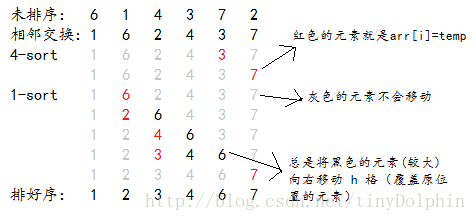
优化之后代码：

    public static void sortPlus(Comparable[] arr) {
        int length = arr.length;
        int h = 1;
        while (h < length / 3) {
            h = 3 * h + 1;  // 1 , 4 , 13 , 40 , 121 , 364 , 1093...
        }
        int exchanges = 0; //交换次数
        //若 arr[index] < arr[index - 1]，则交换两数
        for (int index = length - 1; index > 0; index--) {
            if (less(arr[index], arr[index - 1])) {
                exch(arr, index, index - 1);
                exchanges++;
            }
        }
        //若交换次数为0（即数组有序），则无需进行下一步排序。
        if (exchanges == 0) return;
        //若有交换次数，表明目前的数组无序。
        while (h >= 1) {
            // 将数组变为 h 有序
            for (int indexI = h; indexI < length; indexI++) {
                Comparable temp = arr[indexI];  //记录一下arr[indexI]的值
                int indexJ = indexI;            //indexI 的代替品
                //若 indexJ 的前 h 位元素小于 temp，则将小于temp的元素向右移动 h 位
                //需要注意：可能会出现 indexJ < h 的情况。而一般的插入排序不会出现。
                while (indexJ >= h && less(temp, arr[indexJ - h])) {
                    arr[indexJ] = arr[indexJ - h];
                    indexJ -= h;
                }
                arr[indexJ] = temp; //将记录的值放在 indexJ 的位置上
            }
            h = h / 3;
        }
    }

测试代码：
【高效复制数组的方法】，提示：点击蓝色字体查看方法详情。

    public static void main(String[] args) {
        int length = 10000000;//千万级别
        Integer[] arr = new Integer[length];
        Integer[] arr2 = new Integer[length];
        for (int index = 0; index < length; index++) {
            arr[index] = new Random().nextInt(length) + 1;
        }
        //高效复制数组的方法
        System.arraycopy(arr, 0, arr2, 0, arr.length);

        long start = System.currentTimeMillis();
        sort(arr);  //千万级别-耗费时间：43690ms //百万-耗费时间：2845ms //十万-耗费时间：226ms
        long end = System.currentTimeMillis();
        System.out.println("耗费时间：" + (end - start) + "ms");
        assert isSort(arr);

        start = System.currentTimeMillis();
        sortPlus(arr2); //千万级别-耗费时间：32513ms //百万-耗费时间：1592ms //十万-耗费时间：252ms
        end = System.currentTimeMillis();
        System.out.println("耗费时间：" + (end - start) + "ms");
        assert isSort(arr2);
    }

※由以上测试可知，当数据量越大（超过十万级别）的时候，优化效果越明显。

注意：编译器默认不适用 assert 检测（但是junit测试中适用），所以要使用时要添加参数虚拟机启动参数-ea
具体添加过程，请参照eclipse 和 IDEA 设置虚拟机启动参数